2023.05.28 学习周报

---

摘要

This week, I read a computer science about GNN. The previous approach is insufficient to obtain accurate session vectors and ignore complex transitions between projects. Therefore, a new approach is proposed, which is based on session recommendation and graph neural network. GNN can capture complex item transitions that are difficult to achieve with traditional sequential methods, and then use an attention mechanism to represent each session as a combination of global preferences and the current interests of that session. A large number of experiments show that SR-GNN is significantly superior to some of the most advanced recommended methods. In addition, I learn the content of weighted residual value method of finite element, and learn and think about tensor field and convection-diffusion equation.

本周，我阅读了一篇与GNN相关的文章。由于以前方法不足难以获得准确的会话向量，并且忽略了项目之间的复杂转换。因此，提出了一种新的方法，即基于会话的推荐与图神经网络。GNN可以捕捉到传统序列方法难以实现的复杂项目转移，然后使用注意力机制将每个会话表示为全局偏好和该会话当前兴趣的组合。通过大量实验表明，SR-GNN明显优于最先进的一些推荐方法。此外，我学习了有限元的加权残值法内容，以及学习并思考了张量场和对流-扩散方程的相关内容。

---

文献阅读

1.题目

文献链接：Session-based recommendation with graph neural networks

2.现有方法存在的局限性

文章选择了几种比较有代表性的方法，其中最有代表性的方法是将RNN引入到推荐系统中，这些方法存在局限如下：
1）当一个会话中的用户行为数量十分有限时，RNN就很难捕获到用户的行为表示。在使用RNN建模时，如果前面时序的动作项较少，最后一个输出产生推荐项时的准确性就比较低。
2）在会话过程中，item之间的转移模式在会话推荐中是十分重要的，但是RNN和马尔科夫过程只对相邻物品的单向转移进行了建模，而忽略了会话中的其他item信息。
针对以上两点局限性，文章设计了一个名为SR-GNN的推荐框架，用于会话序列推荐。

3.SR-GNN模型

SR-GNN的模型框架：

1）上图最左侧是输入的数据，每一行表示一个用户进行 物品点击的记录。v表示物品，对于每一行数据可以表示为一个会话，目的是根据这样的用户点击序列，来预测用户下一个要点击的物品。
2）基于每个session去构建一个子图，需要注意的是，每个用户的历史情况都会构建成一个图。
3）使用GNN对图进行信息挖掘，获取session图中每个点击物品的embedding_1，向量化表示为 [v1,v2,…,vn]，其中每个Vi都是一个向量，对应图中红框的结果。
4）对于获得的每个物品的向量化表示，实际上只有最后一个时刻物品是比较重要的，将其取出为s1，而其他的信息会通过注意力分配的机制，添加了attention策略，根据前面几个物品跟最后一次点击的相似度，来进行注意力权值的附加，然后将这些最后一次之间的信息附加权重后加在一起，成为向量sg。
5）最后一步是先对s1和sg进行横向拼接，并进行线性变换，得到结果sh，最后将sh与每个物品的embedding进行内积计算，并通过softmax包装获取得到对应不同物品的点击概率，根据概率的大小绝对最后的推荐物品。

4.模型的组成部分

4.1 构图

构图最主要的工作是如何把用户的历史交互记录，转换成一个有向图。比如用户的点击序列是 v1 -> v2 -> v3 -> v2 -> v4，则其对应的图可以转化成如下的形式。那么为什么将每个用户的行为都包装成一个图呢，因为如果将所有用户对商品的交互关系都放在一张图中，会导致对用户独特兴趣捕捉上的混乱，所以需要单独构建，每一行样本都可以构建成一张图。

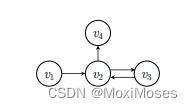
每一个session序列中的item都会根据它点击时间被建模成有向图，其中每个节点表示一个item，每条边表示用户的点击行为。这样，出现在不同session中的item都可以被建模成有向图。当然，在一个有向图中，同一个item是可能重复出现的。文章使用邻接矩阵进行图的存储，为每个图都构建一个出度矩阵、入度矩阵，并为了便于输入到神经网络，对度值进行了归一化处理，如下图所示，其中构建出度矩阵和入度矩阵的原因是为了让模型可以学到丰富的双向关系，而不是简单的单向转移关系。

4.2 item向量表示

通过构造图的方法可以知道会话图的几种特点：有向边，边加权，多个会话序列子图。文章所采用的GNN方法主要是基于门控图神经网络实现：

SR-GNN就是使用GNN针对邻接矩阵学习物品的嵌入向量的过程，通过将所有的会话图送入到GNN网络，就能够得到所有节点的嵌入向量。对于GNN通过GRU得到嵌入向量的过程，即是对GRU不断从前到后不断到收敛的过程，相当于传播过程，之后的生成会话嵌入向量和推荐决策就对应于GNN中的输出过程。

4.3 session向量表示

在得到每个item向量之后，利用这些item向量形成session向量，用于基于会话的推荐。对于整体的图，分为局部向量和全局向量进行考虑，从局部和全局角度进行表达来获得更有效的图向量表达。这里使用了注意力机制，首先得到不同结点的注意力权重ai，之后对不同节点添加不同的注意力获取得到全局的向量嵌入结果，其中W1和W2都是注意力机制中可训练的权重：

最终通过对局部和全局的嵌入向量的级联进行线性变化得到了混合嵌入sh：

4.4 预测模块

在得到了每个会话的嵌入后，可以根据此计算出对于物品集中所有物品下一次点击的预测分数，具体来说就是通过该物品的特征嵌入和会话特征嵌入得到：

基于此可以得到每个物品的点击预测概率，也就是最终的输出：

在模型训练过程中，选择交叉熵损失函数，表示为：

5.实验与分析

5.1 数据集

文章使用了两个数据集：
Yoochoose是取自RecSys challenge 2015，它包含了一串用户点击事件；Diginitica取自CIKM Cup 2016，只使用了它的transactional数据。最后对数据进行了清洗，过滤掉了长度为1的session和出现次数小于5的item。

5.2 比较方法

POP、S-POP、Item - kNN、BPR-MF、FPMC、GRU4REC、NARM、STAMP

5.3 评估指标

1）P@20：被广泛用于衡量预测的准确性。它表示前20个项目中正确推荐的项目的比例。
2）MRR@20：是正确推荐的项目的倒数排名的平均值。当排名超过20时，倒数排名设置为0。MRR度量考虑推荐排名的顺序，其中MRR值大表示排名列表顶部的正确推荐。

5.4 实验结果

1）与基线方法的比较
与各种基线方法相比，SR-GNN在P@20和MRR@20可以达到目前最好的效果。实验结果表明，在这两种不同处理中，SR-GNN可以更好的学习到不同出现时间的session特征。

2）连接方案变体的比较
实验结果表明，这三种连接方案都实现了与STAMP和NARM方法相同的性能，这证实了将会话建模为图的有用性。与SR-GNN相比，对于每个会话，SR-GNN-NGC除了考虑当前会话中的项外，还考虑了其他会话的影响，从而减少了当前会话图中与节点连接度高的边的影响；SR-GNN- fc明确地将所有高阶关系视为直接连接，但性能表现上SR-GNN- fc比SR-GNN差。

3）不同会话嵌入的比较
实验结果表明，混合嵌入方法SR-GNN在三个数据集上都取得了最好的结果，这验证了将当前会话兴趣与长期偏好结合起来的重要性。数据显示SR-GNN-ATT在三个数据集上的平均池化性能优于SR-GNN-AVG，它表明会话可能包含一些不能独立处理的噪声行为，注意力机制有助于从会话数据中提取重要行为以构建长期偏好。SR-GNN-L仍然优于SR-GNN-AVG，并且实现了与SR-GNN-ATT几乎相同的性能，这表明当前兴趣和长期偏好对于基于会话的推荐至关重要。

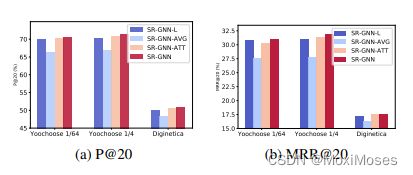
4）会话序列长度分析
进一步分析了不同模型处理不同长度会话的能力，实验证明了该方法的优越性和图神经网络在基于会话的推荐中的适应性。

6.结论

1）对于难以获得用户偏好和历史记录的情况，文章提出了一种新的基于会话的推荐模型架构，将图模型用于表示会话序列。
2）该方法不仅考虑了会话序列项目之间的复杂结构和转换，而且还开发了一种将会话的长期偏好和当前兴趣相结合的策略，以更好地预测用户的下一步行动。
3）通过综合实验证明，该方法始终优于其他最先进的方法。

有限元法

加权残值法：对于没有特别的形状几何和简单的边界条件的情况，可以将其转化为离散模型，从而使解微分方程变成解线性代数方程。

1.一个例子

有一个简单的平衡方程，P为集中载荷，q为分布载荷，ω为挠度。

上面就得到了残差，即与真实情况的差距。下面来看看近似解和真实解：

2.进一步

进行加权残值测试，其中v(x)是试函数，它是任意的，只要它可以被积分。也就是说，如果任意的试函数都让下图积分为0，那么残值肯定为0；否则，对于某些试函数，上面的积分不为0，那么猜的解就不是正解，只能是近似解。

满足一阶导的试函数要比满足二阶导的试函数要好，在原来基础上加上一个倍乘系数，其中一个为自由度，另一个为基函数。

现在加权残值为0，看近似解和真实解：

深度学习

1.张量场

考虑用一个二阶张量场去描述了气体在不同方向上的扩散速率和扩散性质：
1）空间中的每个点都定义了一个二阶张量的场。在每个点上，这个二阶张量可以表示为一个对称正定矩阵，它的特征向量代表了扩散的主要方向，而特征值表示了在这些方向上的扩散速率。
2）这个张量可以表示为：
D(x, y, z) = [[Dxx(x, y, z), Dxy(x, y, z), Dxz(x, y, z)],
[Dxy(x, y, z), Dyy(x, y, z), Dyz(x, y, z)],
[Dxz(x, y, z), Dyz(x, y, z), Dzz(x, y, z)]]
其中：Dxx、Dyy和Dzz是张量的特征值，它们表示在各个坐标轴上的扩散速率。Dxy、Dxz和Dyz是张量的非对角元素，它们表示在不同坐标轴上的耦合扩散。
3）在建立张量场时，需要结合实际观测数据和模型的假设来确定合适的参数和边界条件。通过确定张量场的分布和变化，就可以模拟和预测污染物的扩散行为。

2.对流-扩散方程

结合了对流项和扩散项，可以用来模拟气体在流体介质中的传播和扩散过程。
对流-扩散方程可以写成如下形式：
∂C/∂t + ∇⋅(uC) = ∇⋅(D∇C)
其中：
1）C是气体的浓度，t是时间，u是流体速度矢量，D是扩散系数，∇是梯度运算符，∇⋅是散度运算符。
2）方程的第一项 ∂C/∂t 表示浓度随时间的变化率，对应于气体的生成和衰减过程。
3）方程的第二项 ∇⋅(uC) 表示对流项，描述了流体速度场对气体传播的影响，即表示为流体速度与浓度梯度的点积。
4）方程的第三项 ∇⋅(D∇C) 表示扩散项，描述了气体由于浓度差而发生的自然扩散，即表示成扩散系数D乘以浓度梯度的散度。

---

总结

本周我接触了加权残值法，认识了试函数、基函数，但还没有理解到其中的精髓，只知道它让微分方程变成解线性代数方程，对于计算机来说，求解变得非常简单。此外，我学习了张量场和对流-扩散方程的相关内容，但其中的核心点还没想清楚，以及怎么跟NS方程联系起来还需要去考虑。下周我将继续学习，并思考，加快进度。