【算法题解】34. 二叉树的最小深度

这是一道 简单 题

https://leetcode.cn/problems/minimum-depth-of-binary-tree/

题目

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

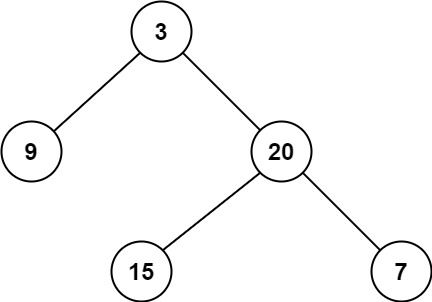
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

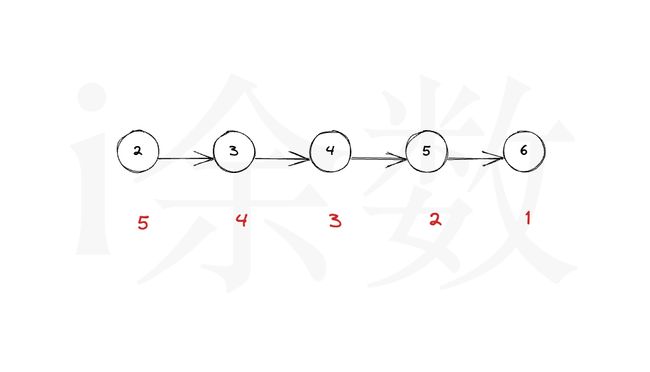
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 $[0,10^5]$ 内
• $-1000<=Node.val<=1000$

简单递归解法

这道题目和 二叉树的最大深度 一样，都可以使用递归解法。

求解公式为： 二叉树的最小深度 = $Min$(左子树的最小深度，右子树的最小深度) + 1。

但是需要注意的是，只有左子树和右子树都不为空的时候才能使用上述公式求解。

如果左子树为空，那么二叉树的最小深度 = 右子树的最小深度 + 1。如下图所示：

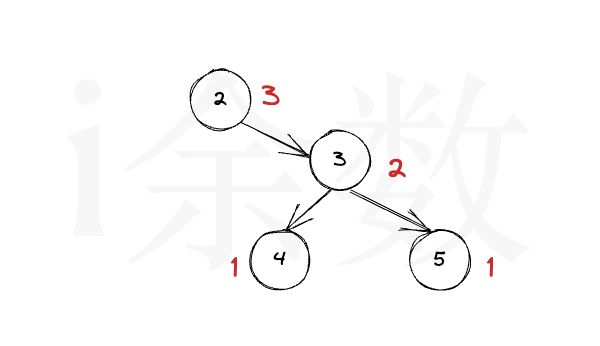
同样的如果右子树为空，那么二叉树的最小深度 = 左子树的最小深度 + 1。

极端情况下会退化成链表，如下图所示：

Java 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if(root == null){
            return 0;
        }

        // 没有子树
        if(root.left == null && root.right == null){
            return 1;
        }

        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);

        if(leftDepth == 0){
            return rightDepth + 1;
        }else if(rightDepth == 0){
            return leftDepth + 1;
        }else {
            return Math.min(leftDepth, rightDepth) + 1;
        }
        
    }
}

Go 代码实现

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minDepth(root *TreeNode) int {

    if root == nil {
        return 0
    }

    if root.Left == nil && root.Right == nil {
        return 1
    }

    leftMin := minDepth(root.Left)
    rightMin := minDepth(root.Right)

    if root.Left == nil {
        return rightMin + 1
    }else if root.Right == nil {
        return leftMin + 1
    }else{
        return min(leftMin, rightMin) + 1
    }

}

func min(a int, b int) int {
    if a < b {
        return a
    }else {
        return b
    }
}

复杂度分析

• 时间复杂度：$O(N)$，N 为二叉树中节点的个数，每个节点都需要计算一次，总共 N 次。
• 空间复杂度：$O(N)$，N 为二叉树中节点的个数，空间复杂度为调用栈的深度，最多为 N ，即二叉树退化成链表的时候。

DFS

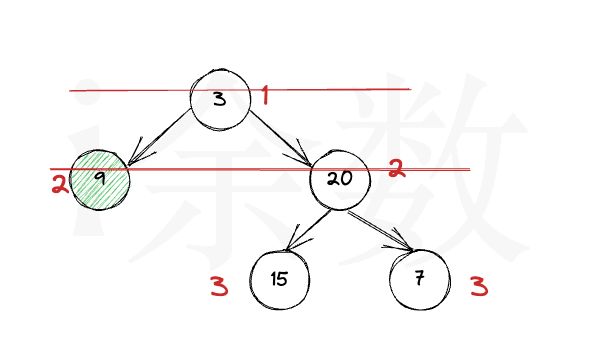
相较于上一步的简单递归解法，深度优先遍历的优点是可以进行剪枝，如下图所示：

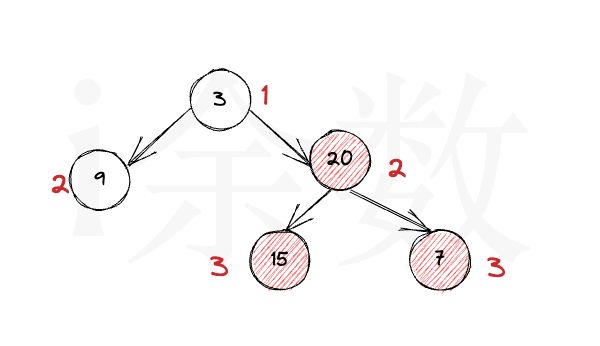
root节点3 到 节点9 的深度是2，那么在遍历到 节点20 的时候深度已经达到2了，后面就无需再遍历，可以直接返回了。

另外需要注意的是边界条件和还原现场：

• 边界条件：碰到叶子结点时计算一次最小深度，并返回。
• 还原现场：depth--，每次回退到上一层的时候深度跟着要减一。

Java 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int depth = 1;
    private int ans = Integer.MAX_VALUE;
    public int minDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        dfs(root);
        return ans; 
    }

    private void dfs(TreeNode node){

        // 剪枝
        if(depth >= ans){
            return;
        }

        // 边界条件，碰到叶子结点计算一次最小深度
        if(node.left == null && node.right == null){
            ans = Math.min(ans, depth);
            return;
        }

        depth++;

        // 遍历左子树
        if(node.left != null){
            dfs(node.left);
        }
        
        // 遍历右子树
        if(node.right != null){
            dfs(node.right);
        }
        
        // 还原现场
        depth--;
        
    }
}

Go 代码实现

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

var (
    depth int
    ans int
)
func minDepth(root *TreeNode) int {

    if root == nil {
        return 0
    }

    depth = 1
    ans = 2 << 32 - 1

    dfs(root)
    
    return ans

}

func dfs(node *TreeNode) {
    // 剪枝
    if depth >= ans {
        return
    }

    // 边界条件
    if node.Left == nil && node.Right == nil {
        ans = min(ans, depth)
        return
    }

    depth++
    if(node.Left != nil){
        dfs(node.Left)
    }
    if(node.Right != nil){
        dfs(node.Right)
    }
    // 还原现场
    depth--
}

func min(a int, b int) int {
    if a < b {
        return a
    }else {
        return b
    }
}

复杂度分析

• 时间复杂度：$O(N)$，N 为二叉树中的节点个数，最差的情况是每个节点都需要遍历一次，总计 N 次。
• 空间复杂度：$O(N)$，N 为二叉树中节点的个数，空间复杂度为调用栈的深度，最多为 N 层。

BFS

广度优先遍历，一层一层的逐层遍历，遇到的第一个叶子结点的深度就是最小深度。

以下图为例，当遍历到 节点9 的时候，就可以直接返回了。

Java 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        int depth = 1;
        queue.offer(root);
        while(!queue.isEmpty()){
            // 同一层节点个数
            int len = queue.size();

            // 将同一层节点全部取出，并将下一层节点入队
            for(int i = 0; i < len; i++){
                TreeNode node = queue.poll();
                // 第一次遇到叶子结点，就是最小深度
                if(node.left == null && node.right == null){
                    return depth;
                }
                // 左子树入队
                TreeNode leftNode = node.left;
                if(leftNode != null){
                    queue.offer(leftNode);
                }

                // 右子树入队
                TreeNode rightNode = node.right;
                if(rightNode != null){
                    queue.offer(rightNode);
                }
            }
            // 同一层节点全部取出后，深度加一
            depth++;
        }
        return depth; 
    }

}

Go 代码实现

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */


func minDepth(root *TreeNode) int {

    if root == nil {
        return 0
    }

    queue := []*TreeNode{root}
    depth := 1

    for len(queue) > 0 {
        // 同一层节点个数
        len := len(queue)
        
        // 将同一层节点全部取出，并将下一层节点入队
        for i := 0; i < len; i++ {
            node := queue[0]
            queue = queue[1:]
            // 第一次遇到叶子结点，就是最小深度
            if node.Left == nil && node.Right == nil {
                return depth
            }
            // 左子树入队
            if node.Left != nil {
                queue = append(queue, node.Left)
            }
            // 右子树入队
            if node.Right != nil {
                queue = append(queue, node.Right)
            }
        }
        // 同一层节点全部取出后，深度加一
        depth++
    }


    return depth
}

复杂度分析

• 时间复杂度：$O(N)$，N 为二叉树中节点的个数，最坏的情况下需要遍历每一个节点。
• 空间复杂度：$O(N)$，N 为二叉树中节点的个数，空间复杂度主要取决于队列的大小，最差的情况就是放 N 个元素。

总结

简单递归解法 的思路最为简单，但是需要计算所有节点，所以效率上不是最好的。

DFS 和 BFS 虽然时间复杂度上也都是$O(N)$，但这是在最坏的情况下得到的，通常都不需要遍历所有节点，所以效率要高一些。

因为 BFS 比 DFS 所需要遍历的节点数会更少一些，所以个人觉得求最小深度（最短路径）的题目使用 BFS 更为合适一些。