Python海龟绘图——分形、递归与递归算法(上)

一、什么分形

    分形，具有以非整数维形式充填空间的形态特征。通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都(至少近似地)是整体缩小后的形状”，即具有自相似的性质。比较正式的定义是：局部和整体按某种方式相似的集合。分形性质包括自相似性、标度不变性，分数维性等。分形(Fractal)一词，是芒德布罗(源于拉丁文形容词fractus，对应的拉丁文动词是frangere(“破碎”、“产生无规碎片”)，以及英文的fraction(“碎片”、“分数”)及fragment(“碎片”)具有相同的词根，在70年代中期以前，芒德布罗一直使用英文fractional一词来表示他的分形思想，故取拉丁词之头，撷英文之尾)创造出来的词(fract+al=fractal)，本意是不规则的、破碎的、分数的。

    中文文献中对芒德布罗的译名一直不统一，芒德布罗是2019年经全国科学技术名词审定委员会审定发布的物理学名词芒德布罗集[合](Mandelbrot set)审定的，有译成芒德勃罗、曼德布罗特等，芒德布罗本人使用的中文名字是“本华·曼德博”(见图1)。芒德布罗(1924-2010)法语原文Benoît B. Mandelbrot，英文名Benoit B. Mandelbrot。

 

图1 Benoît B.Mandelbrot及他的中文签名

    1973年，芒德布罗在法兰西学院讲课时，首次提出了分维和分形的设想。分形理论是当今世界十分风靡和活跃的新理论、新学科。分形的概念是美籍数学家芒德布罗首先提出的。1967年他在美国权威的《科学》杂志上发表了题为《英国的海岸线有多长?》(How longis the coastline of Britain)的著名论文。海岸线作为曲线，其特征是极不规则、极不光滑的，呈现极其蜿蜒复杂的变化。事实上，具有自相似性的形态广泛存在于自然界中，例如：连绵的山川、飘浮的云朵、岩石的断裂口、布朗粒子运动的轨迹、树冠、花菜、大脑皮层……，芒德布罗把这些部分与整体以某种方式相似的形体称为分形(fractal)。如图2中的罗马花椰菜，其上任何上小朵(局部)放大后仍是整棵菜(总体)的极其相似的形状。 

 

(a)整棵花椰菜                                              (b)局部放大

图2 罗马花椰菜，16世纪发现于意大利

    1975年，芒德布罗创立了分形几何学(fractal geometry)。在此基础上，形成了研究分形性质及其应用的科学，称为分形理论(fractal theory)。

    封闭分形图形具有有限面积、无限周长的特性。

二、什么是递归和递归算法

1.递归(Recursion)

    如果一个对象部分地由自己组成，或者是按它自已定义的，则称为是递归的。递归不仅在数学中会遇到，在日常生活中也可以遇到(如图3所示)。

图3 生活中的递归图(两面平行的平面镜产生无穷影像) 

2.递归算法(Recursion Algorithm)

    直接或间接地调用自身的算法称为递归算法。函数调用函数自己的函数称为递归函数。

    递归算法(recursion algorithm)在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题，因此它是计算机科学中十分重要的一个概念。

3、Python绘制分形图

    在Python中可以采用递归算法(递归函数)，使用turtle(海龟)绘制分形图。

1.科赫(Koch)曲线

    科赫曲线的构造过程主要分为三个步骤：(1)给定一个初始图形——一条线段；(2)将这条线段中间的 1/3长度用此长度的无底等边三角形替换(见图4(b))；(3)按照第二步的方法不断的把各段线段中间的 1/3长度用此长度的无底等边三角形替换。这样无限地进行下去，最终即可构造出科赫曲线(如图4所示)。直线段称0阶科赫曲线，经一次替换称1阶科赫曲线，1阶科赫曲线每段直线段再经一次替换，则称为2阶科赫曲线，每多1阶替换，阶数加1，图4中(a)是直线(0阶)、(b)是1阶曲线、(c)是2阶曲线、(d)是3阶曲线、(e)是4阶曲线、(f)是5阶曲线。明显这是个递归过程。 

图4 科赫(Koch)曲线

2.用Python绘制科赫曲线

    由图4(b)可知，设图4(a)直线长度为l，则左转0°(等于没有转向)向前画l/3长直线，左转60°向前画l/3长直线，右转120°(即左转-120°)向前画l/3长直线，左转60°用向前画l/3长直线。由图4(c)可知，设图4(b)直线长度为l，则可重复上述绘图规则绘图。这是个递归问题，每一段直线用4个向左转+向前画指定长度直线的动作完成，每一次用前一次长度的1/3画，直到0阶为止。

    Python用turtle绘制科赫曲线程序代码如下：

 运行结果如图5所示。

图5 6阶科赫曲线

3.科赫(Koch)雪花

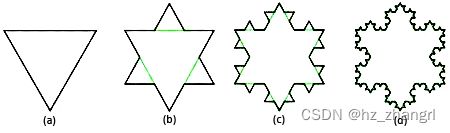
    如图6(a)，一个边长为l的等边三角形，取每边中间的三分之一，接上去一个形状完全相似的但边长为其三分之一的去掉底边的三角形，结果是一个六角形(图6(b))。取六角形的每个边做同样的变换，即在中间三分之一接上更小的去掉底边的三角形(图6(c))，如此重复，直至无穷。边变得越细微曲折，形状接近理想化的雪花(图6(d))。

图6 科赫雪花生成原理图

4.用Python绘制科赫雪花

    如图6(a)所示，一个向下的边长为l的等边三角形，每边按科赫曲线绘制，也就是三条边各按科赫曲线画一遍，就能得到科赫雪花。

Python用turtle绘制科赫雪花程序代码如下：

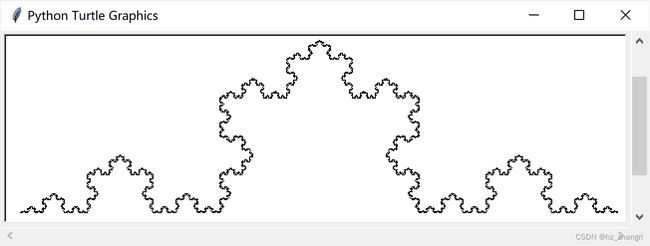
    运行结果如图7所示。

图7 4阶科赫雪花

5.分形二叉树

    如果向上画一条线段，终点向左向右各画一条缩短一些的线，终点向左向右各画一条缩短一些的线，以此类推就可以画出一棵二叉树。第一段线条为树干，其他为枝条，当线条(枝条)长度缩短到一定长度时终止。这也是一个典型的递归算法。

    Python用turtle绘制分形二叉树程序代码如下：

'''绘制分形二叉树'''
import turtle as tl 

def draw_branches(tree_length,tree_angle):
    '''绘制分形二叉树递归函数'''
    if tree_length >= 5:					# 树枝长小于5则结束
        tl.forward(tree_length)				# 往前画树杆、树枝
        tl.right(tree_angle)				# 往右转(先画右侧树枝)
        draw_branches(tree_length * 0.75,tree_angle)	# 画下一枝，树枝长降25%

        tl.left(2 * tree_angle)				# 转向画左，画左侧树枝
        draw_branches(tree_length * 0.75,tree_angle)	# 画下一枝，树枝长降25%

        if tree_length <= 10:				# 树枝长小于10，可以当作树叶
            tl.pencolor('green')			# 树叶部分为绿色
        else:
            tl.pencolor('brown')			# 树干部分为棕色
        tl.rt(tree_angle)					# 回正到上一枝方向
        tl.backward(tree_length)			# 然后往回画，回溯到上一层继续画

if __name__ == '__main__':
    tl.up()
    tl.speed(0)
    tl.lt(90)								# 因为树是往上的，所以先把方向向上
    tl.bk(200)								# 把起点放到树干底部
    tl.pd()
    tl.pencolor('brown')					# 树干部分为棕色
    tree_length = 100						# 设置树干的初始长度为100
    tree_angle = 20							# 树枝分叉角度40°，左右各20°
    draw_branches(tree_length,tree_angle)	# 启动绘图
    tl.exitonclick()						# 点击退出绘图窗口

    运行结果如图8所示，由于分形的自相似性，这个二叉树是完全对称，绘制时用了一种线条粗细，树干显得太细，不太像树。

 图8 简单的分形二叉树

6.树干树枝粗细变化的分形二叉树

    如果在画分形二叉树的基础上，让树干、树枝按等比(也可用等差)变细，并当接近终止画最后的线条时加粗画笔，最后的树叶(叶结点)就会比树枝粗而更像树叶，那就更像一棵树。

    Python用turtle绘制树干、树枝粗细变化的分形二叉树程序代码如下：

'''绘制树干树枝放粗细变化的分形二叉树'''
import turtle as tl 

def draw_branches(tree_length, tree_size, tree_angle):
    '''
    绘制树干树枝放粗细变化的分形二叉树递归函数
    '''
    tl.pensize(tree_size)
    if tree_length >= 5:					# 树枝长小于5则结束
        tl.forward(tree_length)				# 往前画树杆、树枝
        tl.right(tree_angle)				# 往右转(先画右侧树枝)
        # 画右下一枝，树枝长降25%，粗细降15%
        draw_branches(tree_length * 0.75, tree_size * 0.85, tree_angle)
        tl.left(2 * tree_angle)				# 往左转(再画左侧树枝)
        # 画左下一枝，树枝长降25%，粗细降15%
        draw_branches(tree_length * 0.75, tree_size * 0.85, tree_angle)
        if tree_length <= 10:				# 树枝长小于10，可以当作树叶            tl.pencolor('green')
            tl.pencolor('green')			# 树叶部分为绿色
            if tree_length <= 7:			# 树尖端部分
                tl.pensize(3)		        # 让树叶宽一点
            else:
                tl.pensize(tree_size)		# 非树叶原粗细
        else:
            tl.pencolor('brown')			# 树干部分为棕色
        tl.rt(tree_angle)					# 回正到上一枝方向
        tl.backward(tree_length)			# 然后往回画，回溯到上一层继续画

if __name__ == '__main__':
    tl.penup()
    tl.speed(0)
    tl.left(90)								# 因为树是往上的，所以先把方向转上
    tl.backward(200)						# 把起点放到底部
    tl.pendown()
    tl.pencolor('brown')					# 树干部分为棕色
    tree_length = 100						# 设置的树干最长为100
    tree_size = 6							# 设置的最粗树干为6
    tree_angle = 20							# 树枝分叉角度40°，左右20°
    draw_branches(tree_length, tree_size, tree_angle)	# 启动绘图
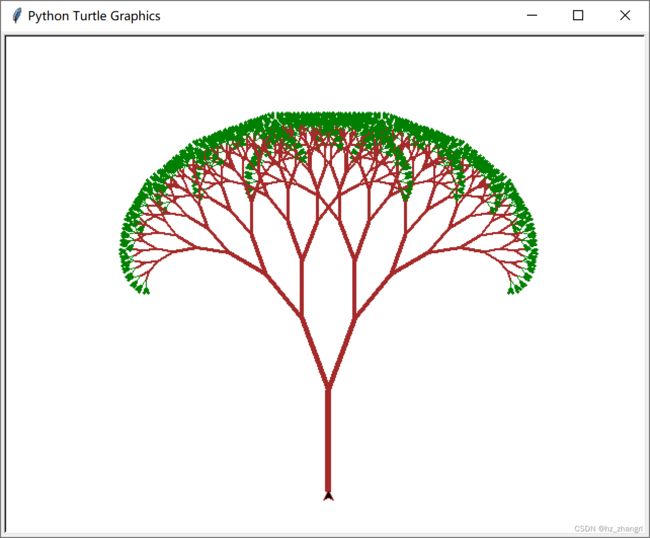
    tl.exitonclick()						# 点击退出绘图窗口

运行结果如图9所示，由于分形的自相似性，这棵树还是完全对称的，比较呆板，但比图8更像一棵树。

 图9 树干、树枝粗细变化的分形二叉树

     如果给树干、树枝长度加上随机数扰动，树枝夹角也加上随机数扰动，那就更像自然的树，因篇幅太长放到下一篇再讲。