人工智能-实验一
第一次实验
一.实验目的
- 掌握有信息搜索策略的算法思想
- 能够编程实现搜索算法
- 应用A*搜索算法求解罗马尼亚问题
二.算法原理
1.A*搜索的评估函数
A算法是一种启发式算法。A*搜索对结点的评估包含两部分,一部分是到达此结点已经花费的代价,记为g(n);另一部分是该结点到目标结点的最小代价的估计值,记为h(n)。因此,经过结点n的最小代价解的估计代价为:
f ( n ) = g ( n ) + h ( n ) f(n) = g(n) + h(n) f(n)=g(n)+h(n)
每次扩展结点时,首先扩展f(n)最小的结点。假设启发式函数h(n)满足特定的条件,则A搜索既是完备的也是最优的。
2.保证最优性的条件
A*算法保证最优性的条件是可采纳性和一致性。
可采纳性是指估计到达目标的代价时,估计值一定小于实际值,即f(n)一定不会超过经过结点n的解的实际代价。因此当搜索到目标结点时,得到的一定是最优解,没有其他结点的估计值更小。
一致性只作用于图搜索。如果对于每一个结点n和通过任一行动a生成n的每个后继结点n’,结点n到达目标的估计代价不大于从n到n’的单步代价与从n’到达目标的估计代价之和。这保证了h(n)是经n到达目标结点的下界。
h ( n ) ≤ c ( n , a , n ′ ) + h ( n ′ ) h(n)\leq c(n,a,n') + h(n') h(n)≤c(n,a,n′)+h(n′)
如果h(n)是可采纳的,则A*进行树搜索是最优的;如果h(n)是一致的,则图搜索的A*算法是最优的。在搜索时,由于A*算法的可采纳性,扩展的结点是下界值最小的,当扩展出目标结点时,得到的一定是最优解。因为目标结点的h(n)=g(n),而这个值小于等于任何其他结点的下界,又根据一致性,之后扩展的目标结点代价不会更低,因此第一个扩展到的目标结点一定是最优解。
3.完备性
完备性要求代价小于等于C*(最优解路径的代价值)的结点是有穷的,每步代价都超过ε并且b是有穷的。
三.求解罗马尼亚问题的算法实现
罗马尼亚问题是一个图的最佳路径搜索问题,可以使用A*算法解决。评估函数 f ( n ) = g ( n ) + h ( n ) f(n)=g(n)+h(n) f(n)=g(n)+h(n),g(n)是到达结点的代价,在扩展结点n时计算,h(n)是结点n距离终点的预计代价,采用直线距离,题中已经给出。由于启发信息h(n)采用直线距离,满足可采纳性和一致性,该搜索方式是最优的。
具体实现时,每个结点需要保存的信息包含g(n),h(n),而f(n)=g(n)+h(n)。由于每次要取出f(n)最小的结点,重载<,便于对结点进行排序。
struct node{
int g;
int h;
int f;
int name;
node(int name, int g, int h){
this->name = name;
this->g = g;
this->h = h;
this->f = g + h;
};
bool operator <(const node &a)const{
return f < a.f;
}
};
图使用邻接矩阵来存储,并可以初始化所有边的信息。
class Graph{
public:
Graph() {memset(graph, -1, sizeof(graph));}
int getEdge(int from, int to) {return graph[from][to];}
void addEdge(int from, int to, int cost){
if (from >= 20 || from < 0 || to >= 20 || to < 0)
return;
graph[from][to] = cost;
}
void init(){
addEdge(O, Z, 71);
...添加所有边
}
private:
int graph[20][20];
};
在搜索过程中,待扩展结点形成一个有序队列,每个结点只扩展一次,需要记录已经扩展过的结点。在初始状态下,每个结点的g(n)值是未知的,因此在扩展当前结点时,要更新当前结点能够到达的所有结点的g(n),保证g(n)取的是到达一个结点的最小代价,为了快速判断更新结点是否在队列中,可以直接记录结点是否在当前队列当中。
bool list[20]; //记录结点是否在当前队列
vector openList; //扩展队列
bool closeList[20]; //记录结点是否扩展过
stack road; //记录路径
int parent[20]; //记录路径
开始搜索时首先将起点入队,只要队列中还有可扩展结点,就不断扩展,当扩展结点为目标结点时,搜索结束。扩展结点时,首先要判断当前结点是否能到达新结点,新结点是否扩展过。如果可扩展新结点,新结点在队列中,则遍历队列找到该结点,尝试更新g(n)和f(n),否则直接构造新结点并加入队列,扩展当前结点结束后,对队列进行排序,保证继续取出f(n)最小的结点扩展。
void A_star(int goal,node &src,Graph &graph){
openList.push_back(src);
sort(openList.begin(), openList.end());
while (!openList.empty()){
/********** Begin **********/
node cur = openList[0];
if(cur.name==goal) return; //取出目标结点,搜索结束
openList.erase(openList.begin());
closeList[cur.name] = true; //当前结点已扩展
list[cur.name] = false; //当前结点出队
for(int i=0;i<20;i++){
if(graph.getEdge(cur.name, i)!=-1 && !closeList[i]){
int cost = cur.g + graph.getEdge(cur.name, i); //到达下一个城市的代价
if(list[i]){
//更新已有结点
for(int j=0;jcost){
openList[j].g = cost;
openList[j].f = openList[j].h + cost;
parent[i] = cur.name;
}
break;
}
}
}
else{
//构造新结点
node newNode(i, cost, h[i]);
openList.push_back(newNode);
list[i] = true;
parent[i] = cur.name;
}
}
}
sort(openList.begin(), openList.end());
/********** End **********/
}
}
搜索结果是最优解。
步骤代价为常数的问题,时间复杂度的增长是最优解所在深度d的函数,可以通过启发式的绝对错误和相对错误分析。绝对误差为 Δ = h ∗ − h Δ=h^*-h Δ=h∗−h, h ∗ h^* h∗为根节点到目标结点的实际代价。在最大绝对误差下,A*的时间复杂度为指数级 O ( b Δ ) O(b^Δ) O(bΔ),每步骤代价为常量,因此可以记为 O ( b ε d ) O(b^{εd}) O(bεd),d为解所在深度。
四.思考题
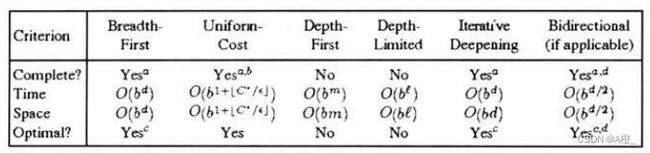
1.宽度优先搜索,深度优先搜索,一致代价搜索,迭代加深的深度优先搜索算法哪种方法最优?
当每一步的行动代价都相等时,宽度优先搜索和迭代加深的深度优先搜索最优,否则一致搜索代价算法最优。宽度优先算法在最浅的目标处于有限深度时是完备的,但只有路径代价是基于结点深度的非递减函数时才是最优的,最典型的就是行动代价相等的情况,迭代加深的深度优先搜索类似,且二者时间复杂度与空间复杂度也相同。一致代价搜索时最优的,扩展路径消耗最小的结点,由于代价非负,第一个被扩展的目标结点一定是最优解。但一致代价搜索可能会探索代价小的行动的搜索树,开销更大。深度优先搜索既不是完备的,也不是最优的。
2.贪婪最佳优先搜索和A*搜索那种方法最优?
A*搜索算法是最优的。贪婪最佳优先算法不具有完备性,也不具有最优性,是否找到最优解与启发式函数有关。而A*搜索算法满足可采纳性和一致性就是最优的,只要分支是有限的就是完备的。
3.分析比较无信息搜索策略和有信息搜索策略。
无信息搜索策略是盲目的搜索,可能需要较大的时间开销和空间开销才能找到解,但是具有好的通用性。有信息搜索策略通过启发式函数利用问题的额外信息,在搜索过程中向着可能有最优解的方向推进,能够提高搜索效率,性能与启发式函数的质量有关。