18.4:打印一个字符串的全部排列
打印一个字符串的全部排列
方法一:暴力方法。
//方法一:暴力方法。
public static List<String> permutation1(String s) {
//str是一个存储字符类型的有序表。
ArrayList<Character> str = new ArrayList<>();
//将字符串中的类型存储在str中。
for (Character c : s.toCharArray()) {
str.add(c);
}
String path = "";
List<String> ans = new LinkedList<>();
process(str, path, ans);
return ans;
}
//str:字符数组。
//path:记录之前选择的答案。
//ans:记录最终的结果。
public static void process(ArrayList<Character> str, String path, List<String> ans) {
if (str.isEmpty()) {
ans.add(path);
return;
}
for (int i = 0; i < str.size(); i++) {
char value = str.get(i);
str.remove(i);
process(str, path + String.valueOf(value), ans);
//还原现场,之前在那就放在哪。
str.add(i, value);
}
}
注意要还原现场,之前在哪个位置,就放回到哪个位置上去,保证原始数据的整洁性。
因为如果数据一旦混乱,就会出现结果的不准确。
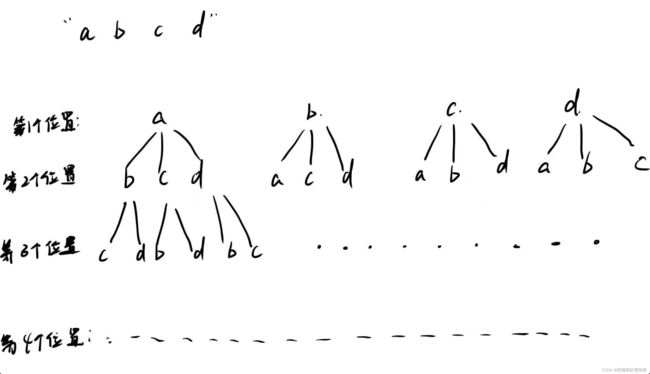
举个例子:
"a b c d " 刚开始选a作为开头,剩下的bcd进入递归,最终将以a为开头的数据记录完成。从递归出来,然后str.add( value);
直接将a尾插,假设现在的 str = bcda,然后i++; i ==1,从str中拿出的下一个数据是c,而不是我想要的b,我们的到的结果都乱了。
由此可知,递归完成出来之后,之前什么位置的数就放回什么位置。这样保证了数据的完整性。
方法二:进行交换的方法。
//方法二:
public static List<String> permutation2(String s) {
char[] str = s.toCharArray();
List<String> ans = new LinkedList<>();
process(str, 0, ans);
return ans;
}
//index:表示的是当前的位置。
public static void process(char[] str, int index, List<String> ans) {
if (index == str.length) {
ans.add(String.valueOf(str));
return;
}
for (int i = index; i < str.length; i++) {
swap(str, index, i);
process(str, index + 1, ans);
//还原现场,之前在那就放在哪。
swap(str, index, i);
}
}
public static void swap(char[] str, int i, int j) {
char temp = str[i];
str[i] = str[j];
str[j] = temp;
}
注意这里还是需要还原现场,之前在哪里的就放回到哪里。
比如:
0跟2交换的时候,a又跑到头上去了,而我想要的是c在头上。之所以出现这种情况是因为数据全乱了,在乱的数据上进行交换,会导致部分结果无法得到。
想得到正确的结果,必须在干净的数据(原始数据)上进行变换,所以每一步操作完了,就还原现场,保证数据跟原始数据一致。
打印一个字符串的全部排列,要求不要出现重复的排列
剪枝策略:
//打印一个字符串的全部排列,要求不要出现重复的排列
public static List<String> permutation3(String s) {
char[] str = s.toCharArray();
List<String> ans = new LinkedList<>();
process2(str, 0, ans);
return ans;
}
public static void process2(char[] str, int index, List<String> ans) {
if (index == str.length) {
ans.add(String.valueOf(str));
return;
}
boolean[] visited = new boolean[256];// ------------------------------------注意
for (int i = index; i < str.length; i++) {
//str[i] -> 找到该字符的ASCII码,visited[str[i]] -> 判断该字符之前是否存在过。
if (!visited[str[i]]) {
visited[str[i]] = true;
swap(str, index, i);
process2(str, index + 1, ans);
//还原现场,之前在那就放在哪。
swap(str, index, i);
}
}
}
boolean[] visited = new boolean[256];这个数组的位置至关重要。
每一层创建一个visited 数组来判断这一层中某个字符是否出现过。并不是全局就创建一个visited 数组如果这样的话,结果就会出现错误。