最短路径算法刷题笔记

Dijkstra最短路算法

理论

代码来自chatgpt，我感觉代码很好，比我在网上找到的好理解很多

#include 
#include 
using namespace std;
const int N = 110;
const int INF = 0x3f3f3f3f;
int n, m;
int g[N][N]; // 邻接矩阵表示图
int dist[N]; // 记录源点到每个点的最短距离
bool vis[N]; // 记录每个点是否已访问
void dijkstra(int s)
{
    memset(vis, false, sizeof(vis));
    memset(dist, INF, sizeof(dist));
    dist[s] = 0;
    for (int i = 0; i < n; i++)
    {
        int u = -1;
        for (int j = 1; j <= n; j++)
            if (!vis[j] && (u == -1 || dist[j] < dist[u]) u = j;//这一步会将离源点最近且没走过的点找出来
        vis[u] = true;
        for (int v = 1; v <= n; v++)
            dist[v] = min(dist[v], dist[u] + g[u][v]);
    }
}
int main()
{
    cin >> n >> m;
    memset(g, INF, sizeof(g));
    for (int i = 1; i <= n; i++) g[i][i] = 0;
    for (int i = 0; i < m; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c); // 无向图
    }
    dijkstra(1);
    for (int i = 1; i <= n; i++) cout << dist[i] << " ";
    cout << endl;
    return 0;
}

带负权则无法处理，不能使用Dijkstra算法

Dijkstra算法以 点 出发。D——点从剩下的点里的最短路dis最小的出发

SPFA单源最短路算法

算是bellman-ford算法

对于稀疏图来说，比Dijkstra算法快
SPFA算法可以用于有负权图有负环则不行
一般能用Dijstra算法则用Dijstra算法

SPFA算法以边出发bellman-ford，b——边 SPFA用到队列，将源点相关联的点放到队列中然后再从队列中的点取寻找
SPFA算法是一种求解单源最短路径的算法，可以处理带有负权边的图。除了使用邻接表来存储图的信息之外，我们还可以使用邻接矩阵来存储图的信息。下面是不使用邻接表，使用邻接矩阵的方式实现SPFA算法的代码，并附有详细注释。

#include 
using namespace std;
const int maxn = 1e5 + 5; // 最大顶点数
const int inf = 0x3f3f3f3f; // 无穷大
int n, m; // 顶点数、边数
int graph[maxn][maxn]; // 邻接矩阵表示
int d[maxn], vis[maxn]; // 源点到各个顶点的最短路径长度、是否在队列中
queue<int> q; // 队列
// SPFA算法
void spfa(int s) {
    memset(d, inf, sizeof(d)); // 初始化源点到其他顶点的最短路径长度为无穷大
    memset(vis, 0, sizeof(vis)); // 初始化所有顶点为不在队列中
    d[s] = 0; // 源点到自己的最短路径长度为0
    vis[s] = 1; // 将源点加入队列中
    q.push(s);
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        vis[x] = 0; // 标记为不在队列中
        for (int y = 1; y <= n; y++) { // 遍历x的所有相邻顶点
            if (graph[x][y] != inf && d[y] > d[x] + graph[x][y]) { // 松弛操作
                d[y] = d[x] + graph[x][y];
                if (!vis[y]) { // 如果y不在队列中，就将y加入队列中
                    vis[y] = 1;
                    q.push(y);
                }
            }
        }
    }
}
int main() {
    cin >> n >> m;
    memset(graph, inf, sizeof(graph)); // 初始化邻接矩阵
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        graph[a][b] = c;
    }
    spfa(1); // 以1为源点进行最短路径计算
    for (int i = 1; i <= n; i++) {
        cout << d[i] << " ";
    }
    cout << endl;
    return 0;
}

在上述代码中，我们使用一个二维数组graph来存储图的信息，其中graph[i][j]表示从顶点i到顶点j的边权重值。初始化时，我们将所有的graph[i][j]都赋值为无穷大，表示该边不存在。在遍历顶点x的所有相邻顶点y时，我们需要判断graph[x][y]是否等于无穷大，如果等于无穷大，那么表示顶点x和y之间不存在边。如果d[y] > d[x] + graph[x][y]，那么就进行松弛操作，并将顶点y加入队列中。

判断负环

需要注意的是，当图中存在负权环时，SPFA算法可能会陷入死循环。此时，我们可以设置一个变量count，表示顶点x进入队列的次数，当count达到n时，就说明顶点x进入队列的次数已经超过了n次，即图中存在负权环。我们可以在代码中加入如下代码来判断：

int count[maxn]; // 记录顶点进入队列的次数
// SPFA算法
void spfa(int s) {
    // 省略部分代码
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        vis[x] = 0; // 标记为不在队列中
        for (int y = 1; y <= n; y++) { // 遍历x的所有相邻顶点
            if (graph[x][y] != inf && d[y] > d[x] + graph[x][y]) { // 松弛操作
                d[y] = d[x] + graph[x][y];
                if (!vis[y]) { // 如果y不在队列中，就将y加入队列中
                    vis[y] = 1;
                    q.push(y);
                    count[y]++;
                    if (count[y] > n) { // 如果顶点y进入队列的次数已经超过了n次，那么就说明存在负权环
                        cout << "图中存在负权环" << endl;
                        return;
                    }
                }
            }
        }
    }
}

Floyd多源最短路算法

只能处理不带负边权的图
用邻接矩阵而不是邻接表

注意循环的顺序：

1. 先循环k
2. 再循环i
3. 最后才是j

可以理解为：先固定一个点，这个点是否出现最短路中。然后再固定 i , j 观察路径，通过枚举出任意两个点的路径，然后再看固定的k点是否出现在其中这样的循环效率更高

这段代码的基本思想就是：最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。

const int MAXN = 100;  // 定义最大节点数
int dist[MAXN][MAXN];   // 定义距离矩阵
void floyd(int n) {     // n为节点数
    // 初始化距离矩阵
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(i == j) {
                dist[i][j] = 0;   // 自己到自己的距离为0
            } else {
                dist[i][j] = INF; // 初始化为无穷大
            }
        }
    }
    // 输入边权值
    int m;  // 边数
    cin >> m;
    for(int i = 1; i <= m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        dist[u][v] = w;   // 有边的节点之间权值为w
    }
    // Floyd算法核心
    for(int k = 1; k <= n; k++) {   // 枚举中间节点
        for(int i = 1; i <= n; i++) {   // 枚举起点
            for(int j = 1; j <= n; j++) {   // 枚举终点
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);   // 更新最短距离
            }
        }
    }
}
int main() {
    int n;  // 节点数
    cin >> n;
    floyd(n);  // 调用Floyd算法
    return 0;
}

次短路问题

练习

[蓝桥杯 2022 国 B] 出差

$\mathrm{A}$ 国有 $N$ 个城市，编号为 $1\dots N$ 小明是编号为 $1$ 的城市中一家公司的员工，今天突然接到了上级通知需要去编号为 $N$ 的城市出差。

由于疫情原因，很多直达的交通方式暂时关闭，小明无法乘坐飞机直接从城市 $1$ 到达城市 $N$，需要通过其他城市进行陆路交通中转。小明通过交通信息网，查询到了 $M$ 条城市之间仍然还开通的路线信息以及每一条路线需要花费的时间。

同样由于疫情原因，小明到达一个城市后需要隔离观察一段时间才能离开该城市前往其他城市。通过网络，小明也查询到了各个城市的隔离信息。（由于小明之前在城市 $1$，因此可以直接离开城市 $1$，不需要隔离）

由于上级要求，小明希望能够尽快赶到城市 $\mathrm{N}$, 因此他求助于你，希望你能帮他规划一条路线，能够在最短时间内到达城市 $N$ 。

输入格式

第 $1$ 行：两个正整数 $N,M$ 表示 A 国的城市数量, $M$ 表示末关闭的路线数量。

第 $2$ 行: $N$ 个正整数，第 $i$ 个整数 $C_i$ 表示到达编号为 $\mathrm{i}$ 的城市后需要隔离的时间。

第 $3\dots M+2$ 行: 每行 $3$ 个正整数, $u,v,c$, 表示有一条城市 $u$ 到城市 $v$ 的双向路线仍然开通着，通过该路线的时间为 $c$。

输出格式

第 $1$ 行：$1$ 个正整数，表示小明从城市 $1$ 出发到达城市 $N$ 的最短时间。（到达城市 $N$，不需要计算城市 $N$ 的隔离时间）

样例输入 #1

4 4
5 7 3 4
1 2 4
1 3 5
2 4 3
3 4 5

样例输出 #1

13

提示

【样例说明】

【评测用例规模与约定】

对于 $100\%$ 的数据, $1\le N\le 1000,1\le M\le 10000,1\le C_i\le 200,1\le u,v\le$ $N,1\le c\le 1000$

蓝桥杯 2022 国赛 B 组 E 题。

思路

• 从1出发到$N$，可以想到$dijkstra$算法（没有负权）。我想的就是经典$dijkstra$算法，题目中说每个城市有隔离时间，所以再$dis$处加上后者城市的隔离时间。最后输出$dis[N]$即可
• 别人的思路：基本与我一样

题解

#include
using namespace std;
const int N=1010;
int gra[N][N];
int dist[N];
int g[N];
bool st[N];
int n,m;
int dijkstra()
{
	 memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + gra[t][j]);
        st[t] = true;
    }
	return dist[n];
}
int main() 
{
	cin>>n>>m;
	for(int i=1;i<=n;++i) cin>>g[i];
	g[n]=0;
	memset(gra, 0x3f, sizeof gra);
	for(int i=1;i<=m;++i){
		int u,v,c;
		cin>>u>>v>>c;
		gra[u][v]=g[v]+c;
		gra[v][u]=g[u]+c;
	}
	cout<<dijkstra()<<endl;
}

邮递员送信

有一个邮递员要送东西，邮局在节点 $1$。他总共要送 $n-1$ 样东西，其目的地分别是节点 $2$ 到节点 $n$。由于这个城市的交通比较繁忙，因此所有的道路都是单行的，共有 $m$ 条道路。这个邮递员每次只能带一样东西，并且运送每件物品过后必须返回邮局。求送完这 $n-1$ 样东西并且最终回到邮局最少需要的时间。

输入格式

第一行包括两个整数，$n$ 和 $m$，表示城市的节点数量和道路数量。

第二行到第 $(m+1)$ 行，每行三个整数，$u,v,w$，表示从 $u$ 到 $v$ 有一条通过时间为 $w$ 的道路。

输出格式

输出仅一行，包含一个整数，为最少需要的时间。

样例输入 #1

5 10
2 3 5
1 5 5
3 5 6
1 2 8
1 3 8
5 3 4
4 1 8
4 5 3
3 5 6
5 4 2

样例输出 #1

83

提示

对于 $30\%$ 的数据，$1\le n\le 200$。

对于 $100\%$ 的数据，$1\le n\le 10^3$，$1\le m\le 10^5$，$1\le u,v\le n$，$1\le w\le 10^4$，输入保证任意两点都能互相到达。

思路

• 看完题目，可以得知：要实现邮递员从 1 到 n-1 是比较简单的，基本就是套模板
• 根据题目不难得知是有向边。从 n-1 到 1 ，如果用spfa算法遍历 n-1 到 1 的话，时间复杂度是O(n³)，大概率TLE。所以不先考虑这个方法
• 考虑建立反图：在邮递员回去的这段中，将图上所有的边取反向，那么从 1 到 n-1 的最短路即是 非反图中 n-1 到 1 的最短路

题解

#include
using namespace std;
const int INF=0x3f3f3f3f;
int n,m,u[100005],v[100005],w[100005],dis[1005],ans=0;
void ford(){
	for(int i=1;i<=n;i++)dis[i]=INF;
	dis[1]=0;
	for(int k=1;k<=n-1;k++){
		for(int i=1;i<=m;i++){
			if(dis[v[i]]>dis[u[i]]+w[i]){
				dis[v[i]]=dis[u[i]]+w[i];
			}
		}
	}
	for(int i=1;i<=n;i++)ans+=dis[i];
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)scanf("%d%d%d",&u[i],&v[i],&w[i]);
	ford();
	for(int i=1;i<=m;i++) swap(u[i],v[i]);
	ford();
	printf("%d\n",ans);
}

[蓝桥杯 2018 国 B] 调手表

小明买了块高端大气上档次的电子手表，他正准备调时间呢。

在 M78 星云，时间的计量单位和地球上不同，M78 星云的一个小时有 $n$ 分钟。

大家都知道，手表只有一个按钮可以把当前的数加一。在调分钟的时候，如果当前显示的数是 $0$，那么按一下按钮就会变成 $1$，再按一次变成 $2$。如果当前的数是 $n-1$，按一次后会变成 $0$。

作为强迫症患者，小明一定要把手表的时间调对。如果手表上的时间比当前时间多 $1$，则要按 $n-1$ 次加一按钮才能调回正确时间。

小明想，如果手表可以再添加一个按钮，表示把当前的数加 $k$ 该多好啊……

他想知道，如果有了这个 $+k$ 按钮，按照最优策略按键，从任意一个分钟数调到另外任意一个分钟数最多要按多少次。

注意，按 $+k$ 按钮时，如果加 $k$ 后数字超过 $n-1,$ 则会对 $n$ 取模。

比如，$n=10,k=6$ 的时候，假设当前时间是 $0$，连按 $2$ 次 $+k$ 按钮，则调为 $2$。

输入格式

一行两个整数 $n,k$，意义如题。

输出格式

一行一个整数。表示：按照最优策略按键，从一个时间调到另一个时间最多要按多少次。

样例输入 #1

5 3

样例输出 #1

2

提示

【样例解释】

如果时间正确则按 $0$ 次。否则要按的次数和操作系列之间的关系如下：

1. +1
2. +1, +1
3. +3
4. +3, +1

【数据约定】

对于 $30\%$ 的数据 $0<k<n\le 5$。

对于 $60\%$ 的数据 $0<k<n\le 100$。

对于 $100\%$ 的数据 $0<k<n\le 10^5$。

时限 3 秒, 256M。蓝桥杯 2018 年第九届国赛

思路

• 我的思考：一开始想到的是动态规划。状态就是方案数，根据题目给出的两个按钮，以数学规律的形式表示状态转移规律

【模板】单源最短路径（标准版）

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

$100\to 60$；

$\text{Ag}\to \text{Cu}$；

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

---

给定一个 $n$ 个点，$m$ 条有向边的带非负权图，请你计算从 $s$ 出发，到每个点的距离。

数据保证你能从 $s$ 出发到任意点。

输入格式

第一行为三个正整数 $n,m,s$。
第二行起 $m$ 行，每行三个非负整数 $u_i,v_i,w_i$，表示从 $u_i$ 到 $v_i$ 有一条权值为 $w_i$ 的有向边。

输出格式

输出一行 $n$ 个空格分隔的非负整数，表示 $s$ 到每个点的距离。

样例输入 #1

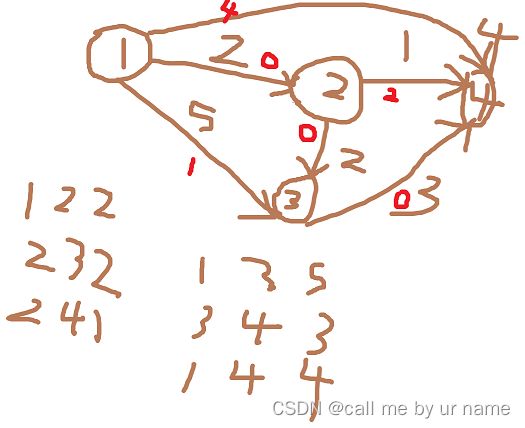
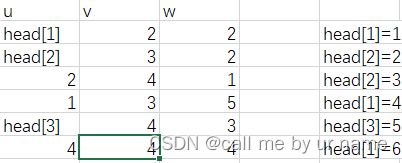
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

0 2 4 3

提示

样例解释请参考 数据随机的模板题。

$1\le n\le 10^5$；

$1\le m\le 2\times 10^5$；

$s=1$；

$1\le u_i,v_i\le n$；

$0\le w_i\le 10^9$,

$0\le \sum w_i\le 10^9$。

思路

• 模板题，用好Dijkstra算法+堆优化
• 虽然Dijkstra算法思想好理解，但是实现起来还是有点复杂的
• 具体看代码注释

题解

#include
const int MaxN = 100010, MaxM = 500010;
struct edge{
    int to, dis, next;
};
edge e[MaxM];
int head[MaxN], dis[MaxN], cnt;
bool vis[MaxN];
int n, m, s;
inline void add_edge( int u, int v, int d ){
    cnt++;
    e[cnt].dis = d;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt; //这个head以链表的形式连接点，分析下面给出的图就会发现，通过head数组即可找到u点连接的所有点
}

struct node{
    int dis;
    int pos;
    bool operator <( const node &x )const
    {
        return x.dis < dis;
    }
};

std::priority_queue<node> q;

inline void dijkstra(){
    dis[s] = 0;
    q.push( ( node ){0, s} );
    while( !q.empty() ){
        node tmp = q.top();
        q.pop();
        int x = tmp.pos, d = tmp.dis;
        if( vis[x] )continue;
        vis[x] = 1;
        for( int i = head[x]; i; i = e[i].next ){     //循环：i=e[i].next就可以发现相关联的点都被连接起来了
            int y = e[i].to;
            if( dis[y] > dis[x] + e[i].dis ){
                dis[y] =std::min(dis[y],dis[x] + e[i].dis);
                if( !vis[y] ) q.push( ( node ){dis[y], y} );
            }
        }
    }
}


int main(){
    scanf( "%d%d%d", &n, &m, &s );
    for(int i = 1; i <= n; ++i)dis[i] = 0x7fffffff;
    for( register int i = 0; i < m; ++i ){
        register int u, v, d;
        scanf( "%d%d%d", &u, &v, &d );
        add_edge( u, v, d );
    }
    dijkstra();
    for( int i = 1; i <= n; i++ )
        printf( "%d ", dis[i] );
    return 0;
}

感觉Dijkstra算法代码和SPFA代码有些相似之处

总结

在解决最短路径问题时，应根据问题的具体情况选择合适的算法，以下是各算法适用情况的简单介绍：

• Dijkstra算法：适用于求解单源最短路径问题，即求解一个点到其他所有点的最短路径，且边权非负。Dijkstra算法通过贪心策略，每次选择当前距离源点最近的未访问点进行松弛操作，从而逐步确定源点到其他点的最短路径。
• SPFA算法：适用于求解单源最短路径问题，且边权可以为负数。SPFA算法基于Bellman-Ford算法，采用队列优化的方式进行松弛操作，可以在某些情况下比Dijkstra算法更快。
• Floyd算法：适用于求解任意两点之间的最短路径，且边权可以为负数。Floyd算法采用动态规划的思想，通过中间点的遍历，逐步确定任意两点之间的最短路径，相对于Dijkstra算法和SPFA算法，Floyd算法的时间复杂度更高，但适用于稠密图。
• 在实际应用中，应根据问题的具体情况选择合适的算法，对于稀疏图，可以使用Dijkstra算法或SPFA算法，对于稠密图或需要求解任意两点之间的最短路径问题，可以使用Floyd算法。