Verilog基础：表达式位宽的确定（位宽拓展）

相关文章

Verilog基础：位宽拓展和有符号数运算的联系

Verilog基础：表达式符号的确定

Verilog基础：数据类型

Verilog基础：case、casex、casez语句

Verilog基础：casex和full_case、parallel_case的使用

Verilog基础：task和function的使用（一）

Verilog基础：task和function的使用（二）

Verilog基础：表达式中的整数常量（integer）

---

表达式位宽

如果想要在计算表达式时获得和谐一致的结果，那么控制表达式中的位宽就很重要。很多时候方法很简单。例如，如果在两个16位数据的reg变量上做位与操作，那么计算结果很显然就是16位。但是在某种情况下，计算应该用多少位或者结果应该是多少位就不那么明显。

例如，对两个16位数据做加法操作是选择用16位进行计算呢，还是为了包含可能的进位而选择用17位进行计算呢？这里就牵扯到了Verilog用来确定表达式位宽的规则。

例1
    reg [15 : 0] a, b;
    reg [15 : 0] sumA;
    reg [16 : 0] sumB;
    sumA = a + b;//赋值表达式右端按照a和b都为16位来计算，结果仍为16位，最后赋值给sumA                                 且进位溢出；
    sumB = a + b;//a和b首先根据规则补零拓展（选择这种拓展是因为赋值表达式右端存在无符号数                              a,b）到17位，然后再执行相加，结果为17位，最后赋值给sumB，因此进位得                                  以保留。

表达式位宽规则

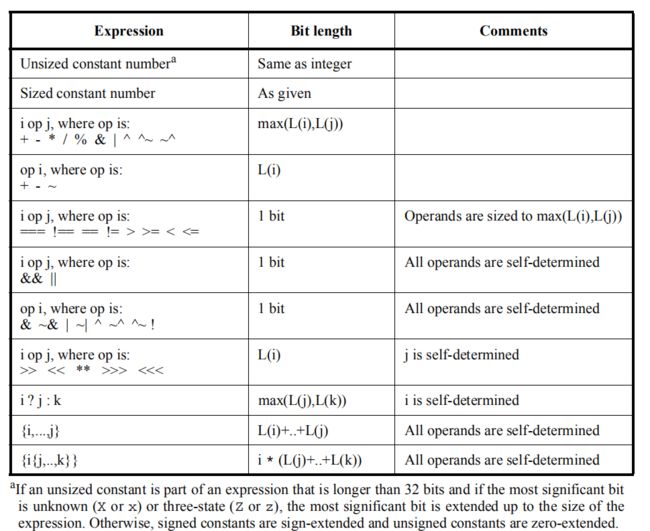
为了在现实的情况下方便地解决位宽问题，Verilog规定了如下的表达式位宽规则。

1. 表达式的位宽由表达式中的操作数本身或表达式所处的上下文决定。Verilog把所有表达式中的操作数分为自决定和上下文决定两类。

2. 自决定表达式（self-determined expression）就是表达式（或整个表达式中的子表达式）中所有操作数的位宽完全由自己决定。

3. 上下文决定表达式（context-determined expression）就是表达式（整个表达式中的子表达式）中所有操作数的位宽由整个表达式上下文环境中最大的位宽决定。

4. 混合自决定和上下文决定表达式就是表达式（或整个表达式中的子表达式）中操作数部分自决定，部分上下文决定。

下图给出了表达式的位宽规则。注：图二来自官方文档。

图一

图二

根据以上两图，我们就可以知道例1的表达式位宽计算过程。首先我们从图1得知，=操作符右端的操作数（不管是单个操作数还是子表达式作为操作数，以下不经特殊说明的操作数均作此解释）是由上下文环境决定位宽的，且根据注释我们还可以得知除了=右端的操作数，=操作符左端的操作数也会加入到上下文环境中。这是什么意思呢？我们可以用例1进行演示。

sumA = a + b;执行这个语句时，+号两端的操作数是上下文环境决定位宽，且=左边也被加入上下文环境，所以sumA，a，b都被加入上下文环境，此时这三个变量的位宽是相同的16位，所以没有数据会拓展，可以直接进行运算，根据图2，a+b结果的位宽为max(L(a), L(b))，所以是16位，进位被舍去，最后将右端的16位值赋给左端的sumA;

sumB=a+b;前面的步骤相同，当sumB，a，b都被加入上下文环境后，最大的位宽为17位，所以a，b首先被位补0拓展至17位，然后再执行加法得到17位的结果，因此保留了进位，最后将右端的17位值赋给左端的sumB;

我们可以多看几个例子来有一个更加形象的认识。

例2
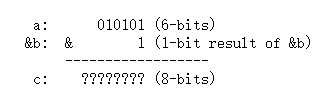
    reg [5 : 0] a = 6'b010101;
    reg [3 : 0] b = 4'b1111;
    reg [7 : 0] c;
    c = a & b;

在例2中，a&b这个自决定作为子表达式成为了=右边的操作数，即是上下文决定位宽的，且我们根据图1又可以知道&运算符两边的操作数也是上下文决定位宽，也就是说，和例1的加法一样，如果一个表达式作为子表达式（或说操作数）会被加入上下文环境（作为=的右操作数），且表达式自己也是上下文决定表达式，那么表达式内部的所有操作数（a，b）都会被加入上下文环境，即上下文环境的嵌套不改变操作数的上下文性质。所以计算过程为：c，a，b都会被加入上下文环境，最大的位宽是8位，所以a，b首先被补零拓展至8位，然后执行按位与运算，根据图2，运算结果仍然是8位，最后将8位结果赋值给左端的c；过程如下面所示。

↓

例3
    reg [5 : 0] a = 6'b010101;
    reg [3 : 0] b = 4'b1111;
    reg [7 : 0] c;
    c = a & (& b);

在例3中，只有最后一步是有变化的，按位与操作符&的右操作数被换成了一个缩减运算子表达式，如果子表达式仍然是上下文决定表达式，那这和上面的两个例子没有任何差别，即a，b，c都会被加入上下文环境，只不过是嵌套的计数不同。但我们从图1，图2都可以注意到，缩减运算符的操作数是自决定的！这时的运算规则就有变化，自决定运算符中的变量不会被加入上下文环境，即b不会被加入上下文环境，而是由自己决定，即b的位宽就是6位，但(&b)作为一整体成为按位与操作符&的右操作数，它的结果的位宽还是会被加入上下文环境(a，c没有这种问题，像上面两例一样被加入上下文环境)。根据上面的规则，我们知道缩减运算的结果是1位，小于c的8位，所以此时最大位宽依然是8位。所以(&b)的结果和a都会被补零拓展至8位，然后按位与，得到结果是8位，最后赋值给c。过程如下面所示。

↓

例4
    reg [15 : 0] a, b, answer;
    answer = (a + b) >> 1;

如果你搞明白了上面三个例子，那么例4你就能自己解决。在看答案前，先自己按照规则尝试着想出表达式的运算过程。

答案：

这里涉及到了一个混合运算符——右移>>，由规则我们可以知道，此运算符的左边即被移操作数为上下文决定，右边即移位量为自决定。我们可以首先找到被加入上下文环境的操作数，a和b作为+操作符的操作数，是上下文决定的，(a+b)作为整体位与移位操作符的左边也是上下文决定的，(a+b)>>1作为整体是=操作符的右操作数，也是上下文决定的，因此answer（因为=），a，b（因为三层上下文嵌套）都被加入上下文环境中，这三个变量的位宽都是一样的，所以他们三个在运算前不会有拓展。因此首先执行a+b，根据规则，结果为16位，进位被丢失，然后再右移一位，最高位补0，最后赋值给同为16位的answer。这里的1（不加基数，位宽的常数）默认是32位，且为自决定。

如果想要进位不被丢失应该怎么样？你可以先自己想一想，方法有很多。

1. 把a+b;改成a+b+0;因为0（32位）此时和a，b一样被加入了上下文环境，所以此时最大位宽为32，所以a，b都会被补零拓展到32位，所以进位得以保留，两次加法结果任然是32位，移位后结果任然是32位，最后将32位值赋值给16位的answer，高位被截断。

2. 把a+b;改成a+b+17'b0;原因同上,此时a，b被补零拓展至17位，所以相加后能保留进位。

3. 把reg [15:0]answer;改为reg [16:0]answer;原因也是类似的，=左端的answer被添加到上下文环境后，最大位宽变为17，此时a，b被补零拓展至17位，所以相加后能保留进位。

例5
    reg [3 : 0] a, b, c;
    reg [4 : 0] d;
    initial begin
        a = 9;
        b = 8;
        c = 1;
        $display("answer = %b", c ? (a & b) : d);
    end

运行结果是什么，为什么是这样？（注意，这里的表达式没有了赋值运算符，这是与之前的例子最大的区别）

运行结果为answer = 01000

从规则中我们知道，三目运算符的第一个操作符（条件项）是自决定的，而第二和第三操作符是上下文环境决定，而在这里第二操作符又是一个以上下文决定子表达式，根据上下文嵌套的规则，a，b和d都被加入上下文环境，最大位宽为5，c不会加入上下文环境，也不会受上下文环境影响。所以a，b被补零拓展为5位，然后执行与运算得到5位结果01000，然后根据c等于1，最后表达式的结果为01000（三目运算符结果的位宽为第二和第三操作数中最大的那个，在此例中都为5）。

例6
    reg [3 : 0] a;
    reg [5 : 0] b;
    reg [15 : 0]c;
    initial begin
        a = 4'hF;
        b = 6'hA;
        $display("a * b = %h", a * b);
        c = {a ** b};
        $display("a ** b = %h", c);
        c = a ** b;
        $display("c = %h", c);
    end

运行结果如下所示:

a * b = 16

a ** b = 1

c = ac61

解析：在第一个系统函数中，只有一个简单的乘式，又因为*两边的操作数是上下文决定的，将a和b加入上下文环境中，最大的位宽为6位，所以a首先被补零拓展到6位，然后和b相乘，结果根据规则，也是6位，假设位宽无限，那么结果为96h也就是10010110b，但是因为结果只取低六位即010110，所以以16进制展现出来就是16。

第二个系统函数用来展示c，c在之前被赋值，c = {a ** b};我们发现a**b居然被放在了拼接运算符里面，这看上去拼接没有什么影响，如果你是这么觉得，你就会得到意想不到的答案。我们一步一步来，**乘方运算符的第一个操作数（底数）是上下文决定的，而第二个操作数（指数）是自决定的，按理说a应该被加入上下文环境，但在这里a**b作为自决定表达式拼接运算符{}的子表达式，所以a与b会被强制转换为自决定，所以在这里，意思就是上下文的嵌套不能穿过自决定表达式，在这里只有{a ** b}会作为=运算符的右操作数和c被加入上下文环境（就像例3一样），所以直接按原本的位宽计算a**b，按照规则，乘方运算结果的位宽与底数位宽相同，所以结果为4位，即取二进制数1000011001000011000010101010110001100001的低4位，也就是0001，上下文环境中最大位宽为16位，所以0001被补零拓展至0000000000000001，最后赋值给c。

最后一个系统函数，展示的是没有拼接运算符{}的赋值结果，此时上下文关系得以传递，a和c都被加入上下文环境，a首先被拓展至16位，然后执行乘方，乘方运算结果的位宽与底数位宽相同，所以结果为16位，即取二进制数1000011001000011000010101010110001100001的低16位，也就是ac61h。

相信通过以上几个例子，你已经可以自己解决关于表达式运算过程中的位宽问题了，但还有一个问题，为什么这里面遇到的都是补零拓展呢，什么时候会遇到符号拓展呢？但这又成为了一个新的专题，有兴趣的同学可以参看我之后的文章。

https://blog.csdn.net/weixin_45791458/article/details/128840843?spm=1001.2014.3001.5502