西瓜书+南瓜书 第三章 线性回归笔记与理解
注：结合南瓜书及其作者的讲解视频，本人对第三章的知识点有了更深刻的理解。在此首先附上南瓜书作者的讲解视频链接：【吃瓜教程】《机器学习公式详解》（南瓜书）与西瓜书公式推导直播合集_哔哩哔哩_bilibili
一、一元线性回归
线性回归试图学得
，使得
. 如何确定 w 和 b 呢？关键在于如何衡量 f (x) 与 y 之间的差别。均方误差是回归任务中最常用的性能度量，我们可以让均方误差最小化，即
求解 w 和 b 使损失函数 
最小化的过程，称为线性回归模型的最小二乘“参数估计”。
二、极大似然估计
下面从极大似然估计的角度推导出损失函数
:
对于线性回归来说也可以假设其为以下模型：
其中 
为随机误差，通常假设其服从正态分布 
，所以 的概率密度函数为
将 用 y - (wx+b) 等价替换，
用极大似然估计来估计 w 和 b 的值
最大化 ln L(w,b) 等价于最小化
也即等价于最小二乘估计。
三、求解 w 和 b
注意：最优化中的凸函数与高数中我们理解的凹函数是一致的，机器学习中的凸函数对应的就是最优化中的凸函数。
如果损失函数 是凸函数,则我们可以通过求偏导的形式求得让 最小的 w 和 b 值。那么如何证明 是凸函数呢？在这里放上一张南瓜书作者对于凸函数的定义的图片。
即去证明 的Hessian矩阵是半正定的。
半正定矩阵的判定定理之一：实对称矩阵的所有顺序主子式均为非负，则该矩阵为半正定矩阵。
经推导 与 
都非负，所以 的Hessian矩阵是半正定的，即 是关于w 和 b 的凸函数。具体推导过程可见视频链接。
分别对 w 和 b 求偏导，并令其等于0，可以得到西瓜书中的公式3.7、3.8。
四、一元线性回归矩阵向量表示
开头讲到，线性回归是求解
在实际应用中，不会按照第三节所讲的那样去求 w 和 b ，matlab 和 python 中都能很方便地进行矩阵运算，因此通常将上式改写为矩阵相乘的形式。
假设有 i 个数据，横坐标 x 和纵坐标 y 已知，要求解的拟合直线方程为：
用向量形式表示为：
， 令
为了让 
最小，已知其为凸函数，对 W 求偏导。
当 
为可逆矩阵时，解得：
注意：对于实矩阵求偏导有以下公式( 
表示N阶单位矩阵 ）：
五、 LOWESS局部加权回归
线性回归思想已经应用在了很多方法和领域里，我目前所接触到的有LOWESS(局部加权回归）、WLS最小二乘法、softmatting(软抠图)等等，下面列举一个在matlab环境下，使用LOWESS对图像直方图进行平滑的例子。
LOWESS与普通线性回归不同的地方在于，LOWESS相比普通线性回归还多了一个权重矩阵，该权重为除主对角线以外全为0的矩阵，形如：
在实验中发现，该权重能够将原本普通线性回归的直线拟合变为曲线，因为对于每个数据点，都要重新计算一个新的权重矩阵，从而每个数据点对应的 w 和 b 都不相同。
对 W 求偏导并令式子为0可得：
下面附上matlab代码：
[filename, pathname] = uigetfile('*','选择origin图片');
filepath = fullfile(pathname, filename);
origin = imread(filepath); %读取图像
[m,n,channel] = size(origin);
hist = imhist(origin); %统计直方图
k = 2;
count = (1:256)';
x = [ ones(length(hist), 1) count ]; %X向量 256 * 2
y = hist; %Y向量 256 * 1
[row,~] = size(x);
[y_out,b,w] = lowess(x,y,k); %调用函数输出
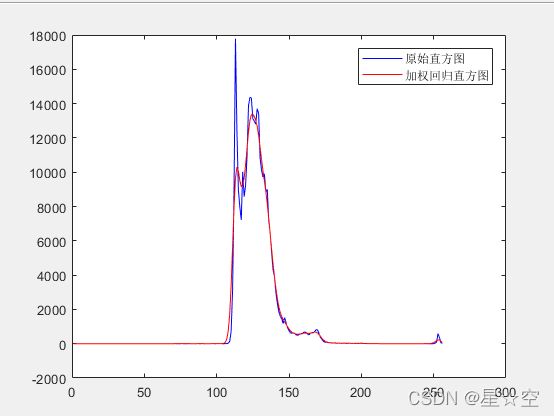
figure,plot(1:256,hist,'g',1:256,y_out,'r');
function [out,b,w] = lowess(x,y,k)
[row,~] = size(x);
out = zeros(1,row);
weights = zeros(row,row);
for i = 1:row
for j = 1:row
diff = x(i,:) - x(j,:);
weights(j,j) = exp(diff * diff'/(-2 * (k.^2))); %对每个点计算权重
end
XTwX = x' * weights * x;
if det(XTwX) == 0
disp('This matrix is singular, cannot do inverse');
end
theta = XTwX^-1 * (x' * weights * y);
b(i) = theta(1);
w(i) = theta(2);
out(i) = x(i,:) * theta;
end
end输出展示：
当不使用权重时，普通线性回归拟合变为直线。
六、多元线性回归
与前面一元线性回归推导过程类似，不再具体推导。
此时要拟合的曲线可能受多个因素影响。
前面提到的 X 就变为西瓜书中所示：
求解W仍然是：
