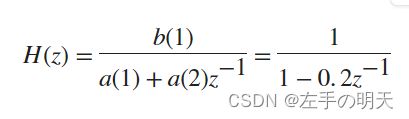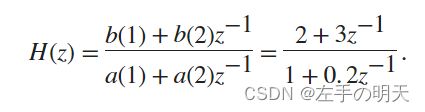【重新定义matlab强大系列六】利用matlab进行一维滤波or二维滤波
运行环境:matlab
撰写作者:左手の明天
精选专栏:《python》
推荐专栏:《算法研究》
#### 防伪水印——左手の明天 ####
大家好,我是左手の明天!好久不见
今天开启新的系列——重新定义matlab强大系列
最近更新:2023 年 05 月 14 日,左手の明天的第 282 篇原创博客
更新于专栏:matlab
#### 防伪水印——左手の明天 ####
目录
filter:1 维数字滤波器
(1)语法
y = filter(b,a,x)
y = filter(b,a,x,zi)
y = filter(b,a,x,zi,dim)
(2)示例
移动平均滤波器
对矩阵行进行滤波
对各部分中的数据进行滤波
filter2:二维数字滤波器
(1)语法
(2)示例
二维台座
filter:1 维数字滤波器
(1)语法
y = filter(b,a,x)
使用由分子和分母系数 b 和 a 定义的 对输入数据 x 进行滤波。
如果 a(1) 不等于 1,则 filter 按 a(1) 对滤波器系数进行归一化。因此,a(1) 必须是非零值。
-
如果
x为向量,则filter将滤波后数据以大小与x相同的向量形式返回。 -
如果
x为矩阵,则filter沿着第一维度操作并返回每列的滤波后的数据。 -
如果
x为多维数组,则filter沿大小不等于 1 的第一个数组维度进行计算。
y = filter(b,a,x,zi)
将初始条件 zi 用于滤波器延迟。zi 的长度必须等于 max(length(a),length(b))-1。
y = filter(b,a,x,zi,dim)
沿维度 dim 进行计算。例如,如果 x 为矩阵,则 filter(b,a,x,zi,2) 返回每行滤波后的数据。
(2)示例
移动平均滤波器
移动平均滤波器是用于对含噪数据进行平滑处理的常用方法。使用 filter 函数计算沿数据向量的平均值。
创建一个由正弦曲线数据组成的 1×100 行向量,其中的正弦曲线被随机干扰所损坏。
t = linspace(-pi,pi,100);
rng default %initialize random number generator
x = sin(t) + 0.25*rand(size(t));移动平均值滤波器沿数据移动长度为 windowSize 的窗口,并计算每个窗口中包含的数据的平均值。以下差分方程定义向量 x 的移动平均值滤波器:
窗口大小为 5 时,计算有理传递函数的分子和分母系数。
windowSize = 5;
b = (1/windowSize)*ones(1,windowSize);
a = 1;求数据的移动平均值,并绘制其对原始数据的图。
y = filter(b,a,x);
plot(t,x)
hold on
plot(t,y)
legend('Input Data','Filtered Data')对矩阵行进行滤波
使用以下有理传递函数对数据的矩阵进行滤波。
创建一个由随机输入数据组成的 2×15 矩阵。
rng default %initialize random number generator
x = rand(2,15);定义有理传递函数的分子和分母系数。
b = 1;
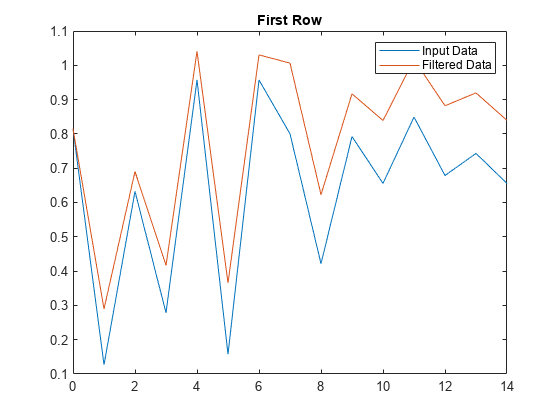
a = [1 -0.2];沿着 x 的第二维度应用传递函数并返回每行的一维数字滤波结果。绘制原始数据的第一行对已滤波数据的图。
y = filter(b,a,x,[],2);
t = 0:length(x)-1; %index vector
plot(t,x(1,:))
hold on
plot(t,y(1,:))
legend('Input Data','Filtered Data')
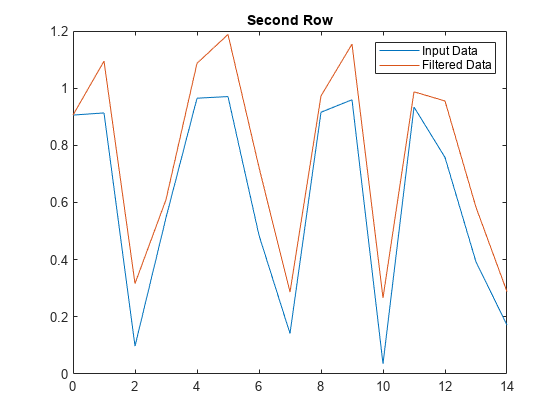
title('First Row')绘制输入数据的第二行对已滤波数据的图。
figure
plot(t,x(2,:))
hold on
plot(t,y(2,:))
legend('Input Data','Filtered Data')
title('Second Row')对各部分中的数据进行滤波
使用滤波器延迟的初始条件和最终条件对各部分中的数据进行滤波,尤其是需要考虑内存限制时请执行此操作。
生成一个大型的随机数据序列并将其拆分为两段:x1 和 x2。
x = randn(10000,1);
x1 = x(1:5000);
x2 = x(5001:end);整个序列 x 是 x1 和 x2 的垂直串联。
定义有理传递函数的分子和分母系数,
b = [2,3];
a = [1,0.2];对子序列 x1 和 x2 进行滤波,一次一个。输出对 x1 进行滤波的最终条件,以便在第一段末尾存储滤波器的内部状态。
[y1,zf] = filter(b,a,x1);将对 x1 进行滤波的最终条件用作对第二段也就是 x2 进行滤波的初始条件。
y2 = filter(b,a,x2,zf);y1 是来自 x1 的滤波后的数据,而 y2 是来自 x2 的滤波
y = filter(b,a,x);
isequal(y,[y1;y2])
ans = logical
1后的数据。整个滤波后的序列是 y1 和 y2 的垂直串联。
同时对整个序列进行滤波以供比较。
filter2:二维数字滤波器
(1)语法
Y = filter2(H,X) 根据矩阵 H 中的系数,对数据矩阵 X 应用有限脉冲响应滤波器。
Y = filter2(H,X,shape ) 根据 shape 返回滤波数据的子区。例如,Y = filter2(H,X,'valid') 仅返回计算的没有补零边缘的滤波数据。
(2)示例
二维台座
使用与 conv2 函数紧密相关的 filter2 函数对图像和其他二维数据进行数字滤波。
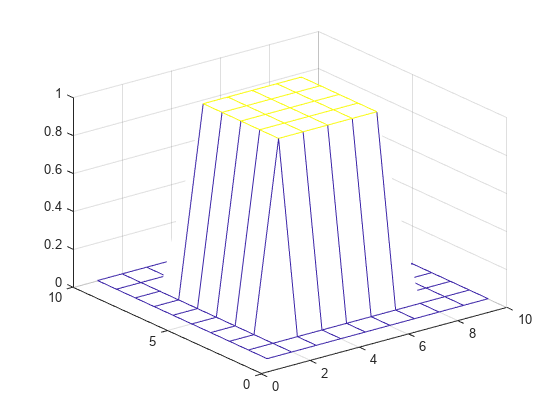
创建并绘制一个内部高度等于 1 的二维台座。
A = zeros(10);
A(3:7,3:7) = ones(5);
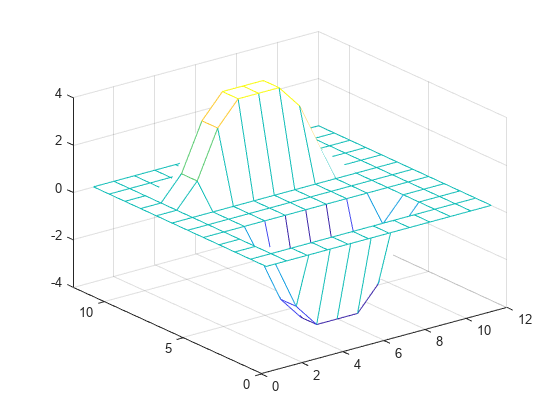
mesh(A)根据滤波器系数矩阵 H 对 A 中的数据进行滤波,并返回已滤波数据的满矩阵。
H = [1 2 1; 0 0 0; -1 -2 -1];
Y = filter2(H,A,'full');
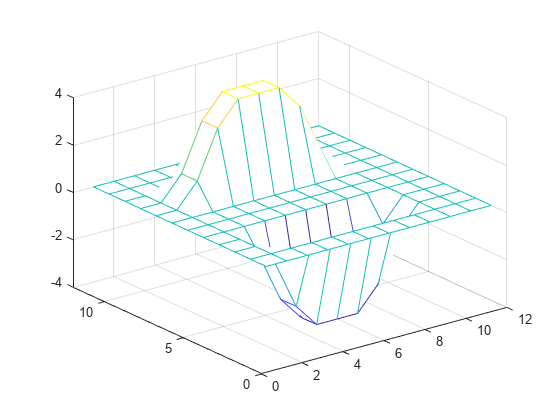
mesh(Y)将 H 旋转 180 度,并将结果与 A 进行卷积。该输出等同于按照 H 中的系数对 A 中的数据进行滤波。
C = conv2(A,rot90(H,2));
mesh(C)
filter2函数通过取输入X的二维卷积和旋转 180 度的系数矩阵H对数据进行滤波。具体而言,就是filter2(H,X,shape)等同于conv2(X,rot90(H,2),shape)。