深度学习神经网络基础知识(三)前向传播，反向传播和计算图

专栏：神经网络复现目录

深度学习神经网络基础知识(三)

本文讲述神经网络基础知识，具体细节讲述前向传播，反向传播和计算图，同时讲解神经网络优化方法：权重衰减，Dropout等方法，最后进行Kaggle实战，具体用一个预测房价的例子使用上述方法。

文章部分文字和代码来自《动手学深度学习》

---

---

前向传播

前向传播（forward propagation或forward pass） ：按顺序（从输入层到输出层）计算和存储神经网络中每层的结果。

在神经网络中，前向传播是指从输入层开始，经过一系列的隐藏层后，将结果输出到输出层的过程。在每一层中，输入会与对应层的权重进行线性组合，再经过激活函数进行非线性变换，得到输出并传递到下一层。这个过程可以表示为：

$$h^{(l)}=f(W^{(l)}{h}^{(l-1)}+b^{(l)})$$

其中，$h^{(l)}$表示第$l$层的输出，$f$为该层的激活函数，$W^{(l)}$为该层的权重矩阵，$h^{(l-1)}$为上一层的输出，$b^{(l)}$为该层的偏置。

在每一层中，输入的维度通常为(batch_size, input_size)，即一批数据的输入维度。而每层输出的维度通常为(batch_size, output_size)，即一批数据的输出维度。这样，一般情况下每一层的权重矩阵的维度为(input_size, output_size)，每一层的偏置的维度为(output_size,)。

前向传播的过程将每层的输出作为下一层的输入，最终得到网络的输出。在训练过程中，输出可以与标签进行比较，计算出网络的误差，并通过反向传播来更新权重和偏置，使得网络的输出更接近于标签。

反向传播

反向传播是一种用于训练神经网络的优化算法，其基本思想是利用链式法则计算损失函数对每个参数的导数，从而更新参数。反向传播中的计算可以通过计算图来表示，其中每个节点代表一个运算，每个边表示数据的传递。

反向传播公式可以表示为：

$$\frac{\partial L}{\partial \mathbf{z}}=\frac{\partial L}{\partial \mathbf{y}}\frac{\partial \mathbf{y}}{\partial \mathbf{z}}$$

其中，$L$是损失函数，$\mathbf{y}$和$\mathbf{z}$是任意两个向量，$\frac{\partial L}{\partial \mathbf{y}}$和$\frac{\partial \mathbf{y}}{\partial \mathbf{z}}$分别是$L$关于$\mathbf{y}$的梯度和$\mathbf{y}$关于$\mathbf{z}$的梯度。

反向传播的主要思想是从输出层开始，计算每一层的梯度，然后根据链式法则将梯度向前传播，最终计算出每个参数的梯度。具体来说，对于每个参数，反向传播算法会计算其对损失函数的梯度，然后使用梯度下降等优化算法来更新参数。

为了更好地理解反向传播算法的推导过程，以下将给出一个简单的两层神经网络的示例，假设输入样本为 $x$，第一层的输出为 $h$，第二层的输出为 $o$，损失函数为 $L$。

首先，根据链式法则，我们可以将输出层的权重 $W_2$ 的梯度表示为：

$$\frac{\partial L}{\partial W_2}=\frac{\partial L}{\partial o}\cdot \frac{\partial o}{\partial W_2}$$

其中，$\frac{\partial L}{\partial o}$ 表示损失函数对输出层输出的偏导数，$\frac{\partial o}{\partial W_2}$ 表示输出层输出对权重的偏导数。

对于 $\frac{\partial L}{\partial o}$，我们可以通过损失函数对输出层输出的偏导数来计算：

$$\frac{\partial L}{\partial o}=\frac{\partial L}{\partial y}\cdot \frac{\partial y}{\partial o}$$

其中，$y$ 表示经过激活函数后的输出，$\frac{\partial L}{\partial y}$ 表示损失函数对 $y$ 的偏导数，$\frac{\partial y}{\partial o}$ 表示 $y$ 对 $o$ 的偏导数。

对于 $\frac{\partial y}{\partial o}$，我们可以根据激活函数的不同，计算出其具体的形式。

对于 $\frac{\partial L}{\partial h}$，我们可以通过链式法则，计算出其表达式：

$$\frac{\partial L}{\partial h}=\frac{\partial L}{\partial o}\cdot \frac{\partial o}{\partial h}$$

其中，$\frac{\partial o}{\partial h}$ 表示输出层输出对隐藏层输出的偏导数。

同样地，我们可以通过链式法则，计算出隐藏层权重 $W_1$ 的梯度：

$$\frac{\partial L}{\partial W_1}=\frac{\partial L}{\partial h}\cdot \frac{\partial h}{\partial W_1}$$

其中，$\frac{\partial h}{\partial W_1}$ 表示隐藏层输出对权重的偏导数。

在实际的反向传播算法中，我们需要依次计算每个参数的梯度，然后利用梯度下降等优化算法来更新参数。

计算图

计算图（computational graph）是用于描述数学表达式中变量之间关系的图形模型，通常用于深度学习中的自动微分。在计算图中，节点表示操作（如加法、乘法、求和、激活函数等），边表示输入和输出之间的关系。计算图可以将复杂的数学表达式拆分成简单的操作，方便求导和计算梯度。

在前向传播时，计算图会按照从输入到输出的顺序依次计算每个节点的输出值。在反向传播时，计算图则按照从输出到输入的顺序依次计算每个节点的梯度，并将梯度传递给其前驱节点。最终，计算图可以通过自动微分技术计算出整个表达式的梯度，并用于优化模型参数。

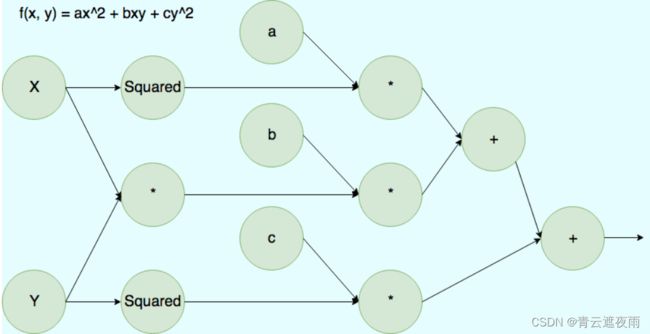
前向传播的计算图

前向传播：节点存储的是计算的值

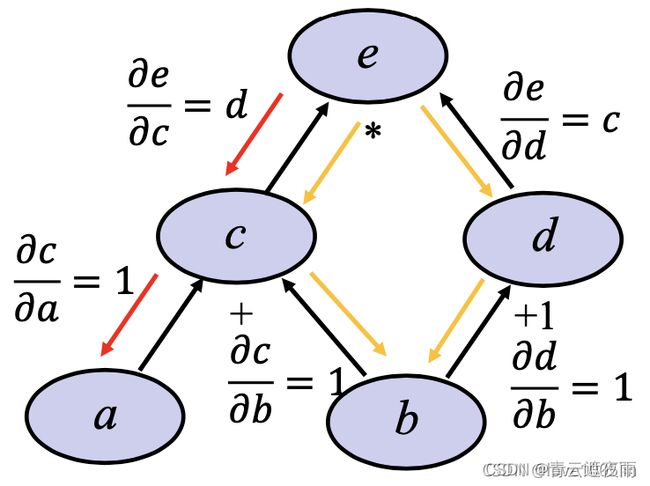
反向传播的计算图

反向传播：节点存储的是此时的梯度

pytorch中的计算图

在 PyTorch 中，计算图是由 torch.autograd 模块负责构建和维护的。该模块提供了一个 Function 类，代表着计算图中的节点，这些节点对应于操作（例如加法、乘法等），并维护了操作的输入、输出和梯度等信息。在计算图中，输入节点称为“叶子节点”，它们对应于输入数据和模型参数。

当我们调用一个函数时，该函数对应的计算图节点将被创建，并用于计算函数的输出。同时，一个新的计算图会在内存中被构建，它会记录该操作与其他操作之间的依赖关系。这个新计算图就是梯度图，我们可以使用它来计算反向传播梯度。

当我们在 PyTorch 中进行自动微分时，每个计算图节点都维护着一个梯度。通过自动微分，我们可以在计算图中反向传播梯度，并且通过对梯度进行链式法则的运算，计算叶子节点的梯度。这些叶子节点的梯度可以用于更新模型参数，以最小化损失函数。

在PyTorch中，Tensor是中心数据结构，它不仅存储数据，还存储计算图中的梯度信息。在每个Tensor上调用.requires_grad=True，可以启用自动微分机制。计算图中每个Tensor都有一个.grad属性，它存储该张量对应的梯度信息。

在计算图中完成前向传播后，可以通过调用.backward()方法来执行反向传播计算梯度。反向传播的过程会沿着计算图反向传播，将梯度信息传递给各个参数Tensor的.grad属性。通过调用优化器的更新方法，即可使用计算出的梯度信息来更新模型的参数。

具体来说，当我们定义一个需要求导的tensor时，PyTorch会为该tensor创建一个计算图，并在图中记录所有计算操作。当我们执行前向传播时，计算图会记录所有执行的操作，以便之后可以根据链式法则计算梯度。然后，当我们执行反向传播时，PyTorch会根据链式法则和计算图中记录的操作来计算梯度。