基于RSSI定位算法的matlab仿真
up目录
一、理论基础
二、核心程序
三、测试结果
一、理论基础
Received Signal Strength Indication接收的信号强度指示,无线发送层的可选部分,用来判定链接质量,以及是否增大广播发送强度。通过接收到的信号强弱测定信号点与接收点的距离,进而根据相应数据进行定位计算的一种定位技术。如无线传感的ZigBee网络CC2431芯片的定位引擎就采用的这种技术、算法。接收机测量电路所得到的接收机输入的平均信号强度指示。这一测量值一般不包括天线增益或传输系统的损耗。
RSSI(Received Signal Strength Indicator)是接收信号的强度指示,它的实现是在反向通道基带接收滤波器之后进行的。为了获取反向信号的特征,在RSSI的具体实现中做了如下处理:在104us内进行基带IQ功率积分得到RSSI的瞬时值;然后在约1秒内对8192个RSSI的瞬时值进行平均得到RSSI的平均值,即RSSI(平均)=sum(RSSI(瞬时))/8192,同时给出1秒内RSSI瞬时值的最大值和RSSI瞬时值大于某一门限时的比率(RSSI瞬时值大于某一门限的个数/8192)。由于 RSSI是通过在数字域进行功率积分而后反推到天线口得到的,反向通道信号传输特性的不一致会影响RSSI的精度。
在空载下看RSSI的平均值是判断干扰的最主要手段。对于新开局,用户很少,空载下的RSSI电平一般小于-105dBm。在业务存在的情况下,有多个业务时RSSI平均值一般不会超过-95dBm。从接收质量FER上也可以参考判断是否有干扰存在。通过以发现是否存在越区覆盖而造成干扰,也可以从 Ec/Io与手机接收功率来判断是否有干扰。对于外界干扰,通过频谱仪分析进一步查出是否存在干扰源。
目前最主要的室内定位算法基本都是脱胎于三角定位算法、指纹定位算法、质心定位算法,前两者的核心思想是通过手机系统的SDK获取到周围各个AP(Access Point)发送的信号强度RSSI(Received Signal Strength Indication 接收信号指示强度))及AP地址,跟据信号衰减模型(信号强度与距离信号源的距离相关)来确定位置,三角定位算法和指纹定位算法使用不同的方式来确定该位置,而质心定位算法则是利用网络的连通性进行定位。
三角定位算法
三角定位算法在需要进行定位的空间放置3个AP,并且3个AP的位置已知,如果知道该空间内某位置的信号强度则可建立信号衰减模型,根据该信号强度计算出该位置到三个AP的距离使用某位置移动设备的信号强度即可估算出其到附近AP的距离,如果能确定若干AP的位置,即可确定该移动设备的位置,显然,三角定位算法只适用于固定场所的定位,并且由于障碍物的存在,信号衰减模型在实际使用时会存在一定误差。
在线定位阶段
在进行定位时,根据实时获取当前RSSI及AP地址,将该信息上传到服务器按一定规则进行匹配,常见的匹配规则有KNN、神经网络、随即森林等等,本质上其实就是分类算法,根据观测数据将RSSI划分到距离类中。
显然,相较三角定位算法,指纹算法更加繁琐,对硬件、算法有着更高的要求,顺理成章的其定位精度也优于三角定位算法。
质心算法
质心算法是一种基于网络连通性的质心定位算法,相较其它算法,其优越之处在于无需测距,其基本思想是:未知节点以所有在其通信范围内锚节点的几何质心作为自己的估计位置。传统的质心算法成本低、计算量小、简单易实现。然而,由于定位精度过度依赖于节点密度,并且精度也较低。为此,很多学者对质心定位算法进行了不同方式的改良,如,基于距离倒数的质心加权和基于RSSI倒数的质心加权算法以及基于最大似然估计的加权质心定位算法。
关于具体的算法理论部分,等后面有时间再进行更新。
二、核心程序
..........................................
for x=1:4
gl1=0;
gl2=0;
gl3=0;
gl4=0;
for m=1:LoopNum
m
%生成移动节点坐标
Dx=BorderHeight.*rand(1,1);
Dy=BorderWidth(x).*rand(1,1);
UN=[Dx,Dy];
for j=1:BeanconAmountA
Beacon(:,j)=[j;(j-1)*Dis;0];%沿区域一侧生成信标节点坐标
distance(:,j)=sqrt((Dx-((j-1)*Dis))^2+Dy^2);%计算移动节点到信标的距离
end
figure(1);
..................................
%用标准RSSI方法测算距离
Loc=LocByRssi(UN,Beacon,distance,BeanconAmountA,R,BigBeacon,Dis,Dx,Dy,m,SBeta);
%用动态路径衰落指数的RSSI方法测算距离
X=LocByDRssi(UN,Beacon,distance,BeanconAmountA,R,BigBeacon,Dis,Dx,Dy,m,SBeta);
%求点位误差、横向误差、纵向误差
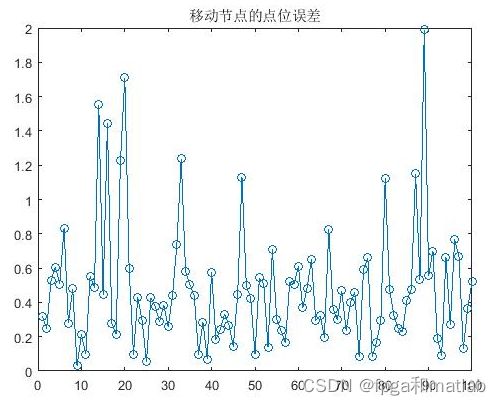
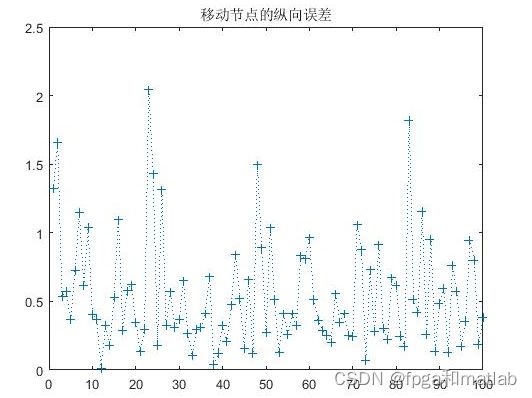
error1(1,m)=sqrt((abs(Dx-X(1)))^2+(abs(Dy-X(2)))^2);
error1(2,m)=abs(X(1)-Dx);
error1(3,m)=abs(X(2)-Dy);
error2(1,m)=sqrt((abs(Dx-Loc(1)))^2+(abs(Dy-Loc(2)))^2);
error2(2,m)=abs(Loc(1)-Dx);
error2(3,m)=abs(Loc(2)-Dy);
%统计两种算法误差落在1m以内的次数
if error1(1,m)<1
gl1=gl1 +1;
end
if error2(1,m)<1
gl2=gl2 +1;
end
%统计两种算法误差落在1.5m以内的次数
if error1(1,m)<1.5
gl3=gl3+1;
end
if error2(1,m)<1.5
gl4=gl4+1;
end
end
end
..................................................三、测试结果
up00013