论文解读：DeepZ：一种用于Z-DNA预测的深度学习方法

标题 DeepZ: A Deep Learning Approach for Z-DNA Prediction.

DOI 10.1007/978-1-0716-3084-6_15

期刊 Methods in molecular biology

作者 Nazar Beknazarov; Maria Poptsova

出版日期 2023-01-01

Github:https://github.com/Nazar1997/Sparse-vector

网址 https://doi.org/10.1007/978-1-0716-3084-6_15

摘要

在这里，我们描述了一种使用深度学习神经网络（如CNN和RNN）从DNA序列中聚合信息的方法；核苷酸的物理、化学和结构特性；组蛋白修饰、甲基化、染色质可及性和转录因子结合位点的组学数据以及其他可用NGS实验的数据。我们解释了如何使用训练的模型对Z-DNA区域进行全基因组注释和特征重要性分析，以确定功能Z-DNA区域的关键决定因素。

数据

        输入数据取自ChIP-seq实验，通常以区间的形式表示（通常以.dad格式）。在我们描述DeepZ模型的原始研究[10]中，我们使用了两个Z-DNA数据集：一个来自ChIP-seq实验，报告了391个Z-DNA区域[4]，第二个数据集由Wu等人[11]和Kouzine等人[12]的数据组成。应该从ENCODE黑名单区域中清除数据集[13]。通常，对于深度学习方法的使用，感兴趣的区域是居中的，并调整到相同的宽度，并被视为正类的对象。在我们的方法中，由于正类中的项目数量较少，我们提出了一种不同的方法。代替间隔，我们考虑核苷酸的水平，其中整个基因组由布尔阵列表示，其中1被分配给Z-DNA区域中的核苷酸，而0被分配给其他区域。通过这种方法，一个小类将包含足够的元素用于机器学习模型（例如，来自ChIP-seq实验的380个Z-DNA区域的位点约150000个，每个位点约400bp长）。第二类是由基因组中的随机位置组成的。

与序列一起，该模型允许合并任何附加信息。这可以是关于二核苷酸的物理、化学或结构性质的信息，以及来自NGS实验的任何组学数据。我们还在DeepZ模型中纳入了最初用于Z-Hunt的B–Z跃迁能（见[14]中的表2），以及关于组蛋白标记（HM）、DNA酶I超敏位点（DNA酶seq）、转录因子（TF）和RNA聚合酶（RNAP）结合位点的额外信息。甲基化变化图取自[15]。

事实上，任何基因组轨迹都可以作为信息层添加（见图1）。在最初的DeepZ出版物中，总的一组包括1058个标记，其中有100个组蛋白标记、947个转录因子结合位点、10个RNA聚合酶结合位点和DNA酶I超敏位点。功能的完整列表可以在[10]中的补充表S1中找到

每个特征都被标准化为区间[0，1]。将整个基因组映射到大小为L×N的矩阵中，其中L是基因组的大小，N是模型中使用的特征数量。人类基因组的总大小超过3×109个核苷酸，需要3 TB的RAM来存储整个矩阵，每个值由4字节的浮点编码。

为了克服这个问题，我们建议使用稀疏向量方法对数据进行压缩。该方法的基本思想是用两个向量对数据进行编码。第一数据矢量直接存储编码矢量的值；第二矢量存储编码矢量中的值的索引。该向量支持以下操作：（1）返回给定切片[i，j]的标准向量值；（2）更改给定切片[i，j]上的向量值。

在真实数据组蛋白数据标签上，压缩级别超过100。因此，大约100兆字节将解决该任务，而不是1兆字节。

对于[10]中描述的具有1058个标记的DeepZ模型，人类基因组的所有数据仅占用约200兆字节。

因此，所有输入数据都可以永久地在RAM中运行。这个包是在Python 3中使用NumPy库实现的，可以在存储库中获得https://github.com/Nazar1997/稀疏矢量。

方法

流程图

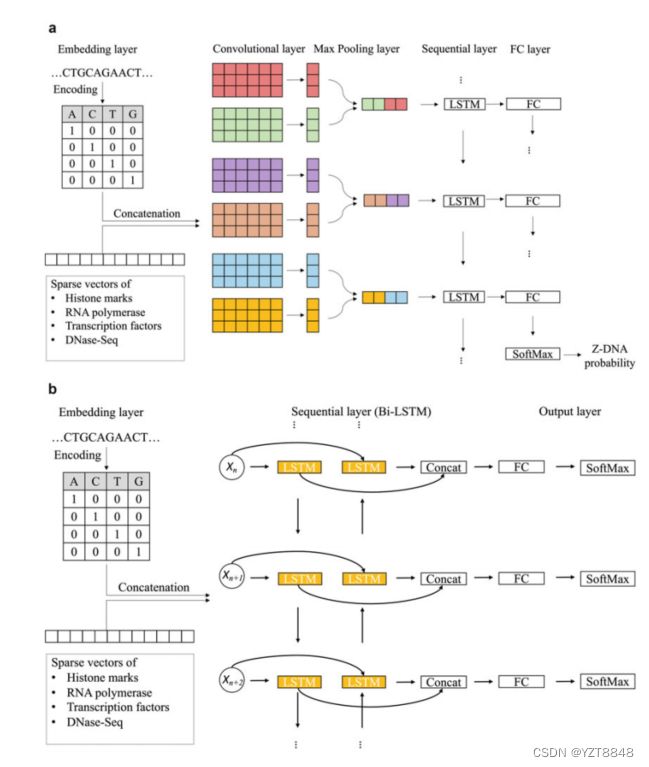
 图1用于Z-DNA预测的深度学习模型的一般模式。

（a） 基于CNN的深度模型架构。

（b） 用于Z-DNA预测的基于RNN的深度模型架构。第二个LSTM单元采用相反的数据顺序，然后将结果与具有原始顺序的第一个LSTM单元格连接，以提高性能

CNN-Based Architecture

这种类型的DL模型仅由CNN和FC层块组成（图1）。尝试了在CNN层之间具有ReLU激活的一个和两个CNN层。卷积核的数量和核的大小从1到17不等。Stride设置为1；填充被设置为（内核大小-1）/2，以保持输出的大小相同。每个卷积核都有1D构象。将CNN块的输出发送到FC块，在FC块中进行最终预测。

RNN-Based Architecture

这种类型的DL模型仅由RNN和FC块组成（图1）。未接触的输入被发送到RNN块。RNN块由具有不同超参数的LSTM网络组成。我们测试了一层和两层LSTM，一层和具有各种隐藏大小的双向LSTM。RNN块的输出被发送到进行最终预测的FC块。

RNN-Based Architecture

这种类型的DL模型由无线网络、有线电视网络和FC块组成。输入首先被发送到CNN块，然后被发送到RNN块，并且在FC块中进行最终预测。搜索每个块的超参数与上述相同。

在最初的DeepZ出版物中，所有模型都是通过反向传播使用RMSprop进行训练的（RMSprop是Geoff Hinton提出的未发表的自适应学习率方法）。

代替全梯度计算，在训练集的子集上计算梯度，并且在每次梯度计算之后相应地更新模型参数。

每个染色体都被分成一组子序列。我们建议避免基于Z-DNA的位点生成子序列的边界，因为当功能元件位于该区域中心时会发生这种情况（见注释1）。每一条染色体都被均匀地切成长度为5000个核苷酸的片段。对于训练集和测试集，我们包括了所有包含Z-DNA的子序列和不包含Z-DNA（从整个基因组中随机选择）的背景序列。随机分组的重复性是固定的。非Z-DNA序列的数量是含Z-DNA序列数量的三倍。训练集和测试集被分层，并以4:1的比例进行划分。分层是基于Z-DNA的存在和染色体数量

一旦模型经过训练，就可以用来预测新的功能性Z-DNA区域。训练DeepZ模型的问题是在开发DeepZ模式时缺乏实验Z-DNA数据。为了最大限度地减少对可用训练集的偏见，我们实施了类似于五倍交叉验证的程序。我们将对此进行进一步详细描述。整个数据集，即整个基因组，被分为5个大小相等的折叠，每个折叠根据染色体数量和Z-DNA存在/不存在的指示（1或0）进行分层。在接下来的每个步骤中，从5个折叠中选择一个用于测试集，并在剩余的4个折叠上训练DeepZ模型。该程序重复进行五次。总共训练了五个DeepZ模型。五个模型中的每一个都用于预测训练集之外的基因组区域。最终预测计算为所有五个模型预测的平均值，这些是核苷酸属于Z-DNA区域的概率。因此，来自每个染色体的每个核苷酸都有可能属于Z-DNA形成区。如果预测的概率高于阈值，我们将核苷酸分配为属于Z-DNA区域。建议选择阈值作为所有5个折叠的组合集上F1得分最大的值（见注2）。

这种方法可以将短DNA区域分配为Z-DNA，这些短DNA区域可以位于彼此短距离处。为了避免片段化，我们将短区域组合成较长的区域，这是基于这样的规则，即考虑到11bp是DNA螺旋的一圈长度，所有间隙小于11bp的间隔都可以连接在一起（见注释3）。

机器学习方法的一个重要方面是所构建模型的可解释性。机器学习模型的价值取决于是否有可能提取有助于模型性能的重要特征。由于RNN架构不适合解释，我们使用了最佳的CNN模型，其性能仅略低于最佳的RNN模型。我们采用了不同的解释方法，并分别进行了描述。

CNN最初是为图像识别而开发的，其中图像以具有像素值的矩阵的形式提供。CNN模型应用不同的滤波器（小矩阵）来揭示图像中的重要元素，而不管它们在图像中的位置如何。在这里，基因组数据被数字化并表示为具有真实值的矩阵，类似于具有像素值的图像表示。应用不同滤波器的想法与图像相同，但这里的重要滤波器对应于循环序列基序。这种从CNN中提取重要过滤器的方法被成功应用于许多工作，包括预测DNA结合位点[16]和其他[8，17]。该方法仅使用转换为感兴趣区域的DNA序列基序特征的序列信息（见注释4）。

从DeepZ模型中获得特征重要性的第二种方法是从组学数据和DNA的物理、化学或结构特性中量化每个特征的积极和消极贡献。为了获得这些值，CNN模型应该单独训练，并具有较高的正则化惩罚。

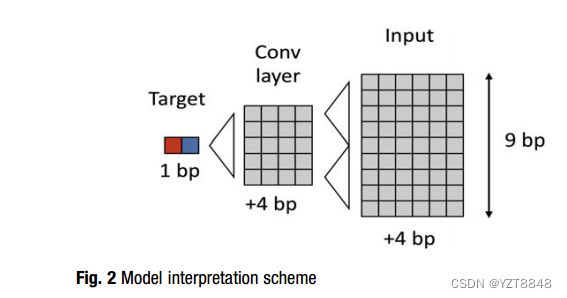
对于图像分类任务，所提出的方法计算类别分数相对于输入图像的梯度[18]。我们的方法类似，不同之处在于输入是核苷酸序列的1D图像。CNN模型的训练是通过在损失函数中添加10-3（或10-2）个L1正则化的权重来完成的。L1正则化具有使所有不必要的模型权重无效的性质，并且在第一卷积层中具有零权重的所有特征被进一步忽略。模型的非零权重被冻结，可训练的输入再次传递给该模型。该模型的结构允许将可训练的输入长度限制为九个核苷酸（图2）。第二层的最远过滤器位于两个核苷酸的距离处；而最远的核苷酸位于距离侧滤器两个核苷酸的距离处。因此，对靶核苷酸的依赖性将不超过向左和向右四个核苷酸。九个元素的序列将完全定义训练后的CNN模型的一个输出，如图2所示。

 结论

然而，与神经网络不同，其权重可以取任何实数，该输入的值只能取0到1之间的值。为了找到从模型的角度增加Z-DNA形成概率的特征，将值的范围设置为-1到1。通过这种方式，我们可以量化具有积极和消极贡献的特征。靶函数使成为中心核苷酸的Z-DNA位点的预测概率最大化。使用学习率为10-2的RMSprop进行输入学习。在每次学习迭代之后，将输入值映射到区间[-1，1]。

在找到使CNN的输出最大化的输入之后，很难找到与其最大输出相对应的DNA序列，因为序列本身是通过单热编码方法编码的。这意味着所有四个输入特征都相互依赖，它们的独立最大化可能会给出与其他特征不同的错误答案。为了找到这样的序列，对编码的序列进行了单独的最大化，但有额外的限制。每个核苷酸的四个特征之和等于一个。有了这些限制，这个问题不是通过普通的梯度下降来解决的，而是通过序列最小二乘规划来解决的。输出是权重矩阵，可以解释为Z-DNA概率（见注释5）。