【CVPR2023】TPS详解：联合令牌剪枝与压缩以实现视觉变形器更积极的压缩

0. 引言

虽然 Vision Transformers （ViTs）近年来在各种计算机视觉任务中展示出良好的效果，但是 Transformers 的高复杂度给计算机资源带来了沉重的负担。ViTs 方面的讲解：ViT 和 基于知识蒸馏的ViT（DeiT）。为了克服 Transformers 存在的问题，众多学者提出了自己的见解。其中主要包括以下几个方面：

1. 最简单的方法（减少Transformers模块比重，增加CNN模块）------MobileViT详解
2. 通过减少模型输入（正确的说：通过Mask的方法减少模型输入，然后通过Encoder-Decoder重构原始图形）。何凯明大神佳作 MAE
3. 通过改变全局注意力计算的方式（Transformers模块复杂度过高往往是由于全局注意力的计算方式）。Swin-Transformer详解、CSWin Transformer详解
4. 通过对令牌进行修剪和合并（通过减少Token的数量进而减少模型复杂度）。DiffRate详解

而本篇文章所提出的新的联合令牌修剪和压缩模块（TPS） ，是为了解决 由修剪策略引起的错误可能导致重大的信息丢失 的问题。首先，TPS通过剪枝得到保留子集和剪枝子集。其次，TPS通过单向最近邻匹配和基于相似性的融合步骤，将被修剪的令牌信息压缩为部分保留令牌。

论文名称：Joint Token Pruning and Squeezing Towards More Aggressive Compression of Vision Transformers
论文地址：https://arxiv.org/abs/2304.10716
代码地址：https://github.com/megvii-research/tps-cvpr2023
注意：截止当前，代码中只有dTPS部分，作者仍在更新完善项目。

1. 为什么要使用TPS？

与传统直接进行令牌修剪相比，联合令牌修剪和压缩在某种程度上保存了所有信息。从而防止因手动设置剪切率导致删除重要信息的情况。

令牌修剪范式(第二行)与联合令牌修剪和压缩(第三行)之间的比较

在上图中，上下文信息(例如示例中的sod)有助于预测，但会被令牌修剪范式丢弃。然而，TPS 方法可以将修剪过的令牌压缩到保留的令牌中，从而减轻了信息丢失。通过这种设计，我们可以应用更积极的令牌修剪，同时减少性能下降。示例结果来自ImageNet1K，为了可视化的清晰度，将实际的补丁网格从 $14\times 14$ 减少到 $7\times 7$。

为了更好地解释 TPS 的操作流程，这里采用图片 对比传统修剪、重组方法和 TPS 方法的区别。

如上图所示，图（a）表示令牌修剪的方法，通过计算各个 token 的重要性，选择其中最为重要的 $k$ 个进行保留，删除余下的 token ；图（b）表示令牌重组的方法，在计算各个 token 的重要性后，将最重要的 $k$ 个进行保留的同时，将需要删除的 token 合并成第 $k+1$ 个 token 进行保存；图（c）表示 TPS 方法，TPS 采用令牌修剪和压缩两步来压缩 ViTs。在TPS 方法中，在计算各个 token 的重要性后，将需要删除的 token 与保留的 token 计算相似性，将需要删除的 token 中存在的信息压缩到最相似的保留的 token 中。
因此，从上述介绍中可知：TPS 方法可以与任意 令牌修剪 的方法相合并，从而得到保留子集 $S^r$ 和修剪子集 $S^p$。

2. TPS介绍

TPS 方法存在两种变体：dTPS和eTPS，分别指 块间（在两个 Transformer Block 之间压缩 token）和块内（在 Transformer Block中间压缩 token）令牌压缩。其中，块间压缩的 Class Token Attention 的理解可以看 DiffRate详解：高效Vision Transformers的可微压缩率。

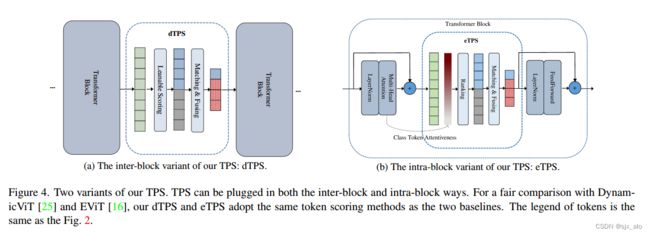
具体而言：

• dTPS 采用dynamicViT 中的可学习令牌分数预测头，通过直通Gumbel Softmax对二值决策掩码进行可微性采样（ 利用Gumbel Softmax,可以使目标函数对于该mask参数可微）;
• eTPS使用类令牌关注值来衡量令牌作为EViT的重要性；
• 在两种变体的推理阶段，基于token分数，使用给定固定token压缩比 $\rho$ 的 Top-k 操作设计token选择策略；
• 这两种变体都保证了恒定的形状，从而从计算图的推理优化中获益。

3. TPS 详解

3.1 重要性计算

论文中作者没有详述重要性计算公式。结合作者给出的代码，相关代码如下所示。

pred_score = self.score_predictor[p_count](
    spatial_x, prev_decision).reshape(B, -1, 2)
if self.training:
    # use gumbel-softmax and mask-attention with policy
    hard_keep_decision = gumbel_softmax(pred_score, hard=True)[
        :, :, 0:1] * prev_decision
    # TODO: dTPS and eTPS
    current_pruned_decision = (
        1-hard_keep_decision) * prev_decision
    spatial_x = self.tps(
        spatial_x, None, hard_keep_decision, current_pruned_decision)
    x = F.concat([x[:, :1, :], spatial_x], axis=1)
    hard_decision_list.append(
        hard_keep_decision.reshape(B, init_n))
    cls_policy = F.ones(
        (B, 1, 1), dtype=hard_keep_decision.dtype, device=hard_keep_decision.device)
    policy = F.concat([cls_policy, hard_keep_decision], axis=1)
    x = blk(x, policy=policy)
    prev_decision = hard_keep_decision
else:
    score = pred_score[:, :, 0]
    num_keep_node = int(init_n * self.keep_ratio_list[p_count])
    sort_idxs = F.argsort(score, descending=True)
    keep_idxs = sort_idxs[:, :num_keep_node]
    drop_idxs = sort_idxs[:, num_keep_node:]
    spatial_x = self.tps(batch_index_select(
        spatial_x, keep_idxs), batch_index_select(spatial_x, drop_idxs), None, None)
    x = F.concat([x[:, :1, :], spatial_x], axis=1)
    x = blk(x)
p_count += 1

上述代码为 dTPS 模型计算重要性， eTPS作者暂未给出。在上述计算过程中，当模型训练的时候使用可学习的分数，然后使用Gumbel Softmax 进行二值决策。当模型训练完成后，采用令牌压缩机制进行操作（类似于DeiT中的知识蒸馏，也许这就是为什么模型文件叫做 tps_deit.py 的原因）。

3.2 令牌压缩

考虑到保留令牌贡献了大部分正确的预测，作者的目的是设计一个过程，在保留大多数注意令牌的同时压缩来自删除令牌的信息，从而保持模型的整体性能。为了避免生成额外的令牌，作者将修剪过的令牌注入到类似的保留令牌中。因此，作者以多对一的方式应用了从 $S^p$ 到 $S^r$ 的单向最近邻匹配算法。然后，作者采用一种基于相似性的融合方法将信息从被修剪的令牌中吸收到部分保留令牌中。
将上述过程概括为两个步骤：匹配和融合。

3.2.1 匹配

给定两个子集 $S^r$ 和 $S^p$ , $I^r$ 和 $I^p$ 是 $S^r$ 和 $S^p$ 对应的 token 序号。对于所有 $i\in I^p$ 和 $j\in I^r$ ，相似度矩阵 $c_{i,j}$ 表示匹配令牌之间的相互作用。对于每一个被删减的令牌 $x_i\in S^p$，从保留令牌集 $S^r$ 中找到距离最近的令牌 $x_{\ast }^{host}\in S^r$ 作为它的 host token:
$$\begin{gathered} x_{\ast }^{host}=argmax{c}_{i,j}(1) \\ {x}_j\in S^r \end{gathered}$$注意，由于令牌匹配步骤从 $S^p$ 到 $S^r$ 是单向的，因此多个被修剪的令牌可以共享同一个主机令牌，而不是每个保留令牌都可以作为主机令牌。
然后，将匹配结果记录在mask 矩阵 $M\in R^{N^p\times N^r}$ 中，其值由下式计算得出:
$$m_{i,j}=\{\begin{array}{l}1，{\mathbf{x}}_{j}isthehosttokenof{\mathbf{x}}_i,\\ 0，otherwise，\end{array}(2)$$式中，$N^p$ 和 $N^p$ 分别表示两个子集的令牌个数。 mask 有助于在排除不匹配对影响的同时，对 $S^r$ 和 $S^p$ 进行规则的矩阵运算来进行以下融合步骤。
虽然注意图是衡量令牌之间相互作用的一种自然而自由的选择，但我们可以通过 $S^r$ 和 $S^p$ 之间的余弦相似度获得更高的性能。因此，在文章的所有的实验中，相似度矩阵定义为:
$$c_{i,j}=\frac{{\mathbf{x}}_i{}^T{\mathbf{x}}_j}{\Vert {\mathbf{x}}_i\Vert \Vert {\mathbf{x}}_j\Vert },fori\in I^p,j\in I^r(3)$$由于相似矩阵 $c_{i,j}$ 是直接由输入特征生成的，所以在匹配步骤中没有引入额外的参数。

3.2.2 融合

由于不同标记之间的差异，简单地平均标记可能导致特性分散。EViT 利用令牌重要性分数来重新加权聚合令牌。因此，作者使用基于相似性的加权方案。它扩大了 closer tokens 对 host tokens 的影响，同时也避免了 impact token 评分带来的潜在缺陷。
如前所述，融合步骤包含来自两个子集的所有令牌，并由 mask $M$ 控制，以确保只混合 host tokens 和已修剪令牌。这引入了一些冗余计算，但由于常规矩阵运算的效率，增加了实际训练和推理吞吐量。
具体来说，通过剪枝保留下来的令牌 $x_j\in S^r$ 通过融合原始特征和被修剪令牌的特征来更新，具体操作如下所示：
$$y_j=w_j{x}_j+\sum _{x_i\in S^p}{w}_i{x}_i,(4)$$其中，$w_i$ 为每个被修剪令牌 $x_i\in S^p$ 的权值，$w_j$ 为保留令牌本身的权值，$y_j$ 为更新后的令牌。融合权值 $w_i$ 取决于掩码值 $m_{i,j}$ 和相似度 $c_{i,j}$，$w_i$ 的具体计算公式如下：
$$w_i=\frac{\exp (c_{i,j})m_{i,j}}{{\sum }_{{\mathbf{x}}_i\in S^p}\exp (c_{i,j})m_{i,j}+\mathrm{e}}(5)$$在计算过程中，保留令牌总是具有最大的融合权值 $w_j$，因为 $x_j$ 与自己的相似度等于1（即 $\exp (c_{i,j})m_{i,j}=\mathrm{e}$），而其余令牌与之相似度小于1。因此， $w_j$ 的计算公式如下所示：
$$w_j=\frac{\mathrm{e}}{{\sum }_{{\mathbf{x}}_i\in S^p}\exp (c_{i,j})m_{i,j}+\mathrm{e}}(6)$$根据上述方程，未被选为 host token 的保留令牌保持不变，而被修剪过的令牌被压缩进 host token ，替换原有令牌。 可以看到，匹配和融合步骤确保处理令牌的数量等于保留令牌的数量，从而保持有效推理的恒定形状。

4. 简化版理解

可能看了上述的内容，大家对于 TPS 的整体还是不太理解。这里对文章内容进行口语式解答来帮助大家理解文章内容。
TPS 这篇文章总的来说通过将需要修剪的信息压缩融合到最近似无需修剪的信息部分（可能存在多个块融合进一个块的情况），既提升了模型的运算速度又不丢失所有信息。
具体而言：

• 首先，确定哪些 token 的重要性较低会被删除，哪些重要性较高会保留。
• 然后，依次匹配需要删除的token与保留的token中哪个最相似。
• 最后，将所有需要删除的token与最相似的保留的token相融合。

注意：可能存在一个保留的token融合多个需要删除token的情况，也存在保留的token与任意一个需要删除toiken也不融合的情况。

5. 总结

作者的实验证明：与最先进的方法相比，TPS方法在所有令牌修剪强度下都优于它们。特别是当将小型计算预算缩减到35%时，与ImageNet分类的基线相比，它的准确率提高了1%-6%。该方法可将DeiT-small的吞吐量提高到超过DeiT-tiny，准确率比DeiT-tiny提高4.78%。在各种变压器上的实验证明了该方法的有效性，分析实验证明了该方法对令牌修剪策略的误差具有较高的鲁棒性。如果有什么疑问欢迎在评论区提出，对于共性问题可能会后续添加到文章介绍中。

到此，有关TPS的内容就基本讲完了。如果觉得这篇文章对你有用，记得点赞、收藏并分享给你的小伙伴们哦。