LeetCode刷题(贪心算法)
1.分发饼干
得排序一下。
class Solution {
public int findContentChildren(int[] g, int[] s) {
int count1=0;//用来记录满足了几个人
int count2=s.length;//记录一下,我们的饼干还剩多少
Arrays.sort(g);//这里得排序一下
Arrays.sort(s);
for(int i=0;i=g[j]&&g[j]!=0&&count2>0){
count1++;
g[j]=0;
count2--;
break;//这里得break一下,因为里面这个饼干找到了主人
}
}
return count1;
}
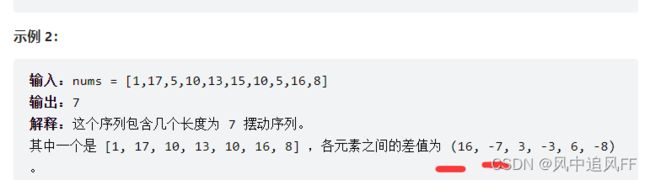
} 2.摆动序列
这个序列里,差值一正一负的。
class Solution {
//只需要让当前差值与上一个差值,符号不一样即可。
public int wiggleMaxLength(int[] nums) {
if (nums.length <= 1) {
return nums.length;
}
//当前差值
int curDiff = 0;
//上一个差值
int preDiff = 0;
int count = 1;
for (int i = 1; i < nums.length; i++) {
//得到当前差值
curDiff = nums[i] - nums[i - 1];
//所有的差值,可以看成一个新的数组。如果i这个位置满足,那就 count++;如果不满足那就下一个i+1
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
count++;
preDiff = curDiff;
}
}
return count;
}
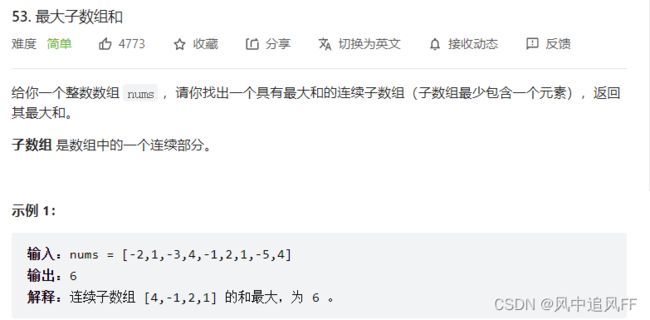
}3.最大子序和(一组数连续相邻和的最大值)
累加的结果为负数,直接让count等于0。重新开始累加。
其实从1那里,count已经<0了,已经从1那里从头开始了。然后1和-3的和小于0。
因为4之前的结果累加是负数。
class Solution {
//思路:遇到负数,一定要重头开始count
//我的卡壳:我认为,卡壳的时候得回到区间起始的地方的下一位。得两层for
public int maxSubArray(int[] nums) {
if (nums.length == 1){
return nums[0];
}
int sum = Integer.MIN_VALUE;//让sum取最小值先。
int count = 0;//记录增长的数量,当增长降到0以下的时候。就是最大和
for (int i = 0; i < nums.length; i++){
count += nums[i];
sum = Math.max(sum, count); // 取区间累计的最大值(相当于不断确定最大子序终止位置)
if (count <= 0){
count = 0;
//确保了重新开始的地方,如果不从这重新开始,前面的负数累积和,可能会拖累整体的结果。
}
}
return sum;
}
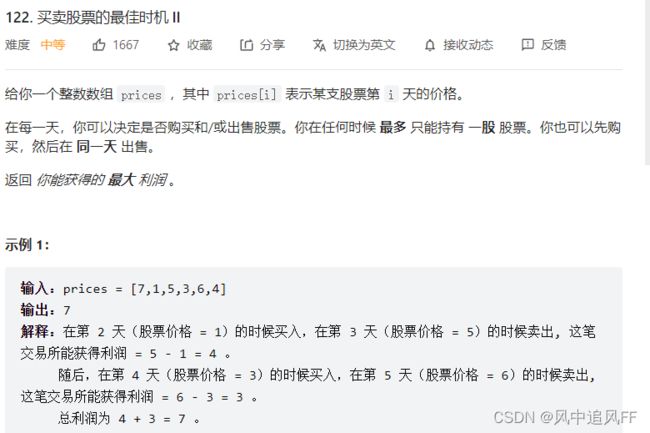
}4.买卖股票的最佳时机
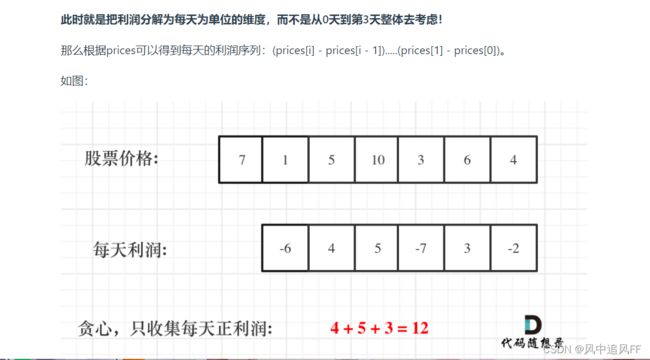
思路:只需要把相邻两天的利润做成一张表。只收集正利润即可。
class Solution {
//看看差值最大呗。但是这个差值可以累计。
//先挑一天,最大差值的那一天,算上这个差值。然后再从这一天继续出发。找它之后最大的差值。再相加
public int maxProfit(int[] prices) {
int[] profit=new int [prices.length-1];
for(int i=0;i0){
sum+=profit[i];
}
}
return sum;
}
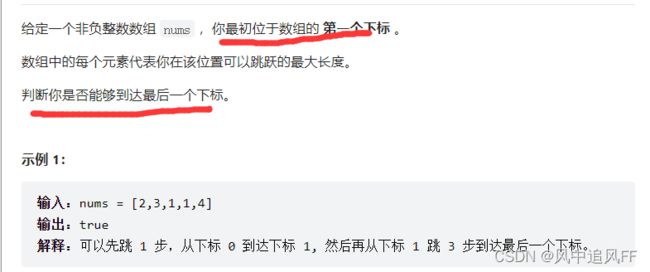
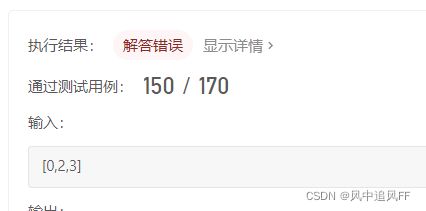
} 5.跳跃问题
思路:在能跳的范围内,看看跳的最远能不能超过最后一位的下标。
class Solution {
public boolean canJump(int[] nums) {
if(nums.length==1){
return true;
}
int len=0;//能跳多远。
//在能跳范围内,更新最大的能跳范围
for(int i=0;i<=len;i++){
len=Math.max(len,i+nums[i]);//求出来,活动范围。
if(len>=nums.length-1){
return true;
}
}
return false;
}
 注意这里,for的上限,是能跳的范围。这个能跳的范围会逐步更新。
注意这里,for的上限,是能跳的范围。这个能跳的范围会逐步更新。
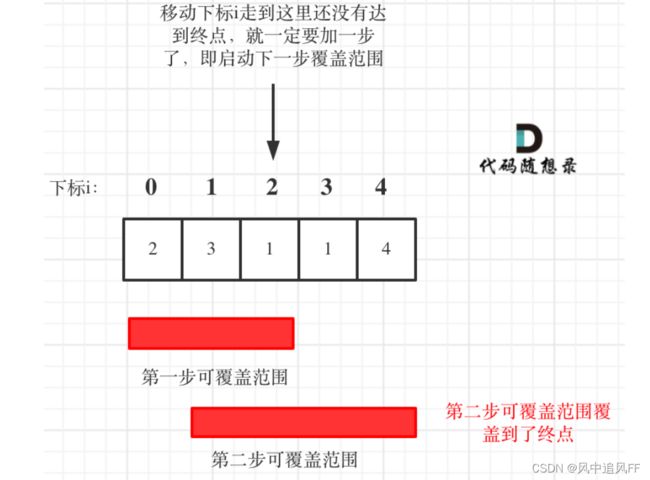
6.跳跃问题二
如果第一步的覆盖范围,走到了尽头,还没有到终点,那就开始走第二步,判断第二步的覆盖范围,是否包括终点。
思路:走当前的层。当走到当前层最后一个地方,还是没能到终点,就到跳到下一层。
走当前层的时候,每走一步都会更新下一层最远到的地方,走到当前层的最后一个地方,下一层要走的,也就更新完毕了。
class Solution {
public int jump(int[] nums) {
if (nums == null || nums.length == 0 || nums.length == 1) {
return 0;
}
int count=0;//当前步数。
int curDistance=0;//站在起点能走的最远的。第一层
int maxDistance=0;//走完第一层,最大的就会更新。然后走第二层。count++。如果走第二层时,maxDisrance刷新了,>=终点下标。
for(int i=0;i=nums.length -1){
count++;
return count;
}
if(i==curDistance){
curDistance=maxDistance;//进入下个区域
count++;
}
}
return count;
}
} 7.k次取反后最大数组和
情况分好,一步步做就行。
class Solution {
//排序一下,找到正负分割的地方,如果有0,记录0的位置。
//情况1,负数的个数》=k,从前到后全部反转。
//情况2,负数的个数《k,取反的次数会多余,2.1:如果剩余次数是2的倍数,不用管。2.2如果或剩余次数对2取余为1,那么,如果有0,全部作用于0;如果没有0,比较正负分割的那两个数的下标的值。看看哪个小,让哪个变成负数。
//情况3,如果没有负数,就看看k对二取余的情况。
public int largestSumAfterKNegations(int[] nums, int k) {
int fu=0;//负数的个数
Boolean flag=false;//看看是否有0这个位。
Arrays.sort(nums);
for(int i=0;i=k){
for(int i=0;i0&&fu=nums[fu]){
nums[fu]=-nums[fu];
return sum(nums);
}else{
nums[fu-1]=-nums[fu-1];
return sum(nums);
}
}else{//不存在整数
nums[fu-1]=-nums[fu-1];
return sum(nums);
}
}
}
}else if(fu==0){
int a=k%2;
if(a==0){
return sum(nums);
}else{//对k取余为1时。
if(flag){
return sum(nums);
}else{
nums[0]=-nums[0];
return sum(nums);
}
}
}
return sum(nums);
}
int sum(int[] nums){
int s=0;
for(int num:nums){
s+=num;
}
return s;
}
} 8.加油站(不好理解)
C++的暴力解法,挨个走一遍。
class Solution {
public:
int canCompleteCircuit(vector& gas, vector& cost) {
for (int i = 0; i < cost.size(); i++) {
int rest = gas[i] - cost[i]; // 记录剩余油量
int index = (i + 1) % cost.size();
while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈
rest += gas[index] - cost[index];
index = (index + 1) % cost.size();
}
// 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置
if (rest >= 0 && index == i) return i;
}
return -1;
}
}; 一个for循环的优化。
// 思路,cursum来记录从开始点出发,剩余的油量。
//当前油量如果小于0了,那么就让下一站作为起始点curSum = 0;。如果走剩下几站,油箱里累加多出来的,能填补前面几站产生的负数,那就说明,能走一圈。
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int curSum=0;
int totalSum=0;
int index=0;//用来记录出发的起点
for(int i=0;i9.柠檬水找零
class Solution {
public boolean lemonadeChange(int[] bills) {
int count5=0;//记录5美元的数量
int count10=0;//记录10美元的数量
for(int i=0;i=1&&count10>=1){//先找给别人10块的,没10再给5。
count5--;
count10--;
continue;
}else{
if(count5>=3){//优先找10块。
count5-=3;
}else{
return false;
}
}
}
}
return true;
}
} 10.根据身高重建队列
遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
queue[j] = [hj, kj] 。people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
先确定还是k先确定h呢,也就是究竟先按h排序呢,还先按照k排序呢?
思路:先把身高都排好序,然后按身高H的优先级。重新往队列里插入。按照身高排序之后,优先按身高高的people的k来插入,后序插入节点也不会影响前面已经插入的节点,最终按照k的规则完成了队列。
那为什么让k当下标插入呢?因为已经让最高的先进去了。后面来的矮的位次就由k决定了。
class Solution {
public int[][] reconstructQueue(int[][] people) {
// 身高从大到小排(身高相同k小的站前面)
Arrays.sort(people, (a, b) -> {
if (a[0] == b[0]) return a[1] - b[1];
return b[0] - a[0];
});
LinkedList que = new LinkedList<>();
//后面按k插入,k就是插入的下标。
for (int[] p : people) {
que.add(p[1],p);//LinkedList这个add方法(本质是链表的插入)。插入,就伴随着后面元素都往后移动一位。
}
return que.toArray(new int[people.length][]);
}
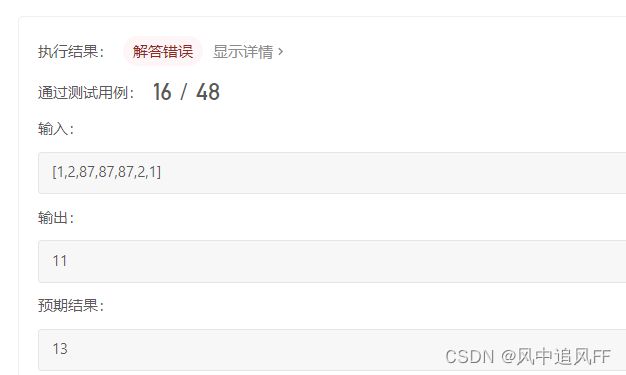
} 11.分发糖果
刚开始的错误思路:给所有的孩子都一个,挨个遍历相邻,谁大,就再给谁一个。这个思路错误的,如果是1,2,3,这3个孩子最终得到的糖果是,1+2+3=6,而不是5+2。
正确思路:每次比较两个,确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
先从左到右,考虑右边的。确定左孩子大于右孩子的情况一定要从后向前遍历!
如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个。
class Solution {
public int candy(int[] ratings) {
int len=ratings.length;
int[] a=new int[len];//整个数组记录孩子们的奖励情况
a[0]=1;
//先处理右边,从左到右,每俩只看右边。
for(int i=0;iratings[i]){
a[i+1]=a[i]+1;
}else{
a[i+1]=1;
}
}
//再处理左边,从右到左,每俩只看左边。
for(int i=len-1;i>=1;i--)
if(ratings[i-1]>ratings[i]){
if(a[i-1] 12.用最少的箭射爆气球。
首先得对这这个气球数组,排序一下。按照第一个元素排序。
13,24,这俩就是可以被连续射爆的,区间有交集。每次判断相邻两个,如果能有交集,就能一起被射爆。
如果没有交集,只能多一发箭,继续判断剩下的相邻。
注意:13,24,56,如果在5.6位,没能一起射爆,那第一箭也影响不到后面的气球,因为已经排序了。
class Solution {
//如果有交集,17,26,34算一只箭。每次判断为同一只箭后,将气球的第二元素,改成第一箭的第二元素。
public int findMinArrowShots(int[][] points) {
//o1,o2长度为2的数组,代表气球的区间。
Arrays.sort(points,(o1,o2)->Integer.compare(o1[0],o2[0]));
//从第二位开始判断,第一位肯定要射出一发箭。
int count=1;
for(int i=1;ipoints[i-1][1]){
count++;
}else{
//如果有交集,那就让后面这个气球,的第二个元素,记录一下,这一箭的边界。边界就是前一个的第二个元素。
points[i][1]=Math.min(points[i][1],points[i-1][1]);
}
}
return count;
}
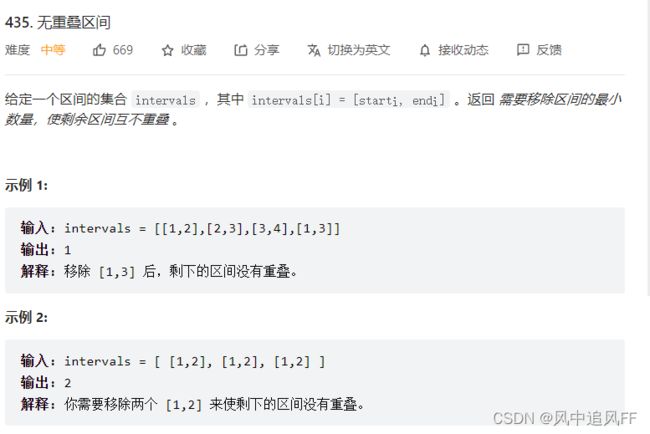
} 13.移除重叠区间
首先得让区间都按规则排序一下,然后挨个比较。如果重叠,则count+1.
如果没有重叠更新右边界。
下面算法比较右边界的,所以让右边界升序即可。。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals,(a,b)->{
return a[1]-b[1];//让右边界排,按升序,
});
int count=0;
//如果是比较右边界的,让右边界升序。
//找个变量记录一下右边界。如果下一个区间的,左边界,大于记录的右边界,那么它就重叠了。就除掉它。
int edge=Integer.MIN_VALUE;
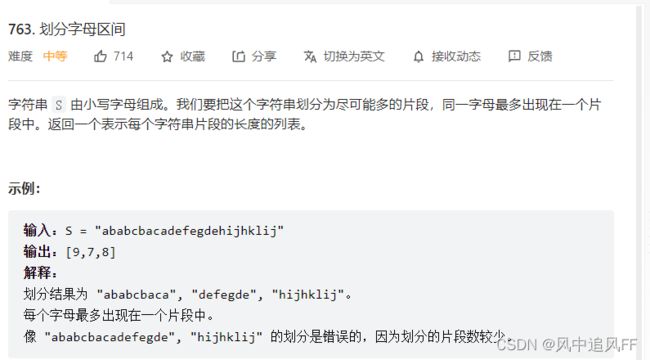
for(int i=0;i14.划分字母区间
class Solution {
//思路:比如我们在找a的结尾的时候,不可避免的让别的字母也进来了。比如b,最终要到的右边界在变大。
//右边界在找a的结尾时,不断变大,当我们亲自走到这个这个边界的时候,就说明,这个时候该add了。
public List partitionLabels(String s) {
List list=new ArrayList<>();
Map map=new HashMap<>();
for(int i=0;imax) max=a;//不断的更新最大的终点,当来到最大的地方的时候,就add进去。
if(i==max){
list.add(len);
len=0;
continue;
}
}
return list;
}
} 15.合并区间
合并所有重叠的区间,返回一个不重叠的。先将区间排序一下,如果这俩有交集,新生成一个大区间。
class Solution {
public int[][] merge(int[][] intervals) {
LinkedList list=new LinkedList<>();
Arrays.sort(intervals,(a,b)->{
if(a[0]==b[0]) return a[1]-b[1];
return a[0]-b[0];
});
//这里严格排序一下。
list.addLast(intervals[0]);
//考虑重复重叠的问题。不断与栈顶的数组做比较
for(int i=1;i 16.单调递增的数字
有暴力解法。从后往前,挨个判断是否是最近的递增。
class Solution {
public int monotoneIncreasingDigits(int n) {
int k=n;
while(true){
if(work(k)){
break;
}
k--;
}
return k;
}
//判断k是否单调递增。
Boolean work(int k){
List list=new ArrayList<>();
while(k!=0){
list.add(k%10);
k=k/10;
}
for(int i=0;i 非暴力解法:在数组上进行修改,找到最左面那个开始大于后面的下标,让它减1。然后这个下标之后的都为9。
class Solution {
//找到start位,让它减1,然后后面的全都变成9,就行。
public int monotoneIncreasingDigits(int n) {
String s = String.valueOf(n);
char[] chars = s.toCharArray();
int start9 = s.length();
for (int i = s.length() - 2; i >= 0; i--) {
if (chars[i] > chars[i + 1]) {//找到最左面开始不满足的位,让那个位减1。
chars[i]--;
/
start9 = i+1;//9开始的地方。
}
//最终让最左面的那个地方停在start。让start位减了1。
}
for (int i = start9; i < s.length(); i++) {
chars[i] = '9';
}
return Integer.parseInt(String.valueOf(chars));
}
}17.监控整个二叉树
摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。
此时,大体思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
此时这道题目还有两个难点:
- 二叉树的遍历:用后序,可以从底到上。
- 如何隔两个节点放一个摄像头。
第二个难点:结点有3个情况。
情况1:该结点已经被摄像头覆盖,有覆盖
情况2:这个结点已经有摄像头。
情况3:这个结点没有被摄像头覆盖,没覆盖
那如果访问到空结点,它是什么状态?
空结点,不能是没覆盖,不然它上面一层的叶子结点,就得安摄像头了。所以访问到空结点的时候,返回它是被覆盖的。
// 空节点,该节点有覆盖
if (cur == NULL) return 2;我们从下往上整。
有4种情况。
1:左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了(从下网上呗)。
![]()
// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;2.左右子至少有一个没有被覆盖。这个时候,这个中间结点就必须得安摄像头了。
if (left == 0 || right == 0) {
result++;
return 1;
}3.左右孩子至少有一个有摄像头。
那这个左右孩子的父亲就得改成是覆盖的状态了。
4.整个过程处理完了之后,最后对根结点,判断一下。是否被覆盖。
如果没有被覆盖,就给他加一个摄像头。
这种情况是,两个子都是被覆盖的,而不是有一个摄像头。
int minCameraCover(TreeNode* root) {
result = 0;
if (traversal(root) == 0) { // root 无覆盖
result++;
}
return result;
}
class Solution {
int res=0;
public int minCameraCover(TreeNode root) {
if(travel(root)==0){
res++;
}
return res;
}
//三种状态,0表示无覆盖,1表示有摄像头,2表示被覆盖。只要子里没被覆盖,就要安摄像头。
int travel(TreeNode root){
if(root==null){
return 2;//避免叶子结点被安摄像头,让叶子结点的儿子,返回2。
}
int left=travel(root.left);
int right=travel(root.right);
if(left==2&&right==2){//如果俩都被覆盖了,说明这个结点肯定还没被覆盖到。
return 0;
}else if(left==0||right==0){//如果有一个没覆盖的,就要装一波摄像头。
res++;
return 1;
}else {//除了上面两种情况,剩下的都是至少有一个摄像头的。记住上面俩种情况即可
return 2;
}
}
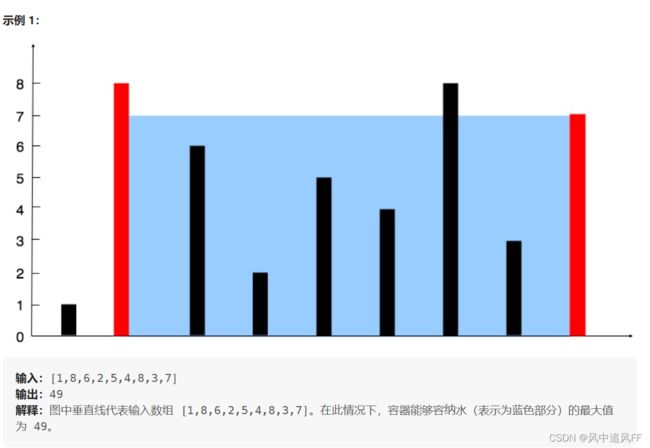
}18. 盛最多水的容器
找两根线,看这两根线能构成的最大的容器量。
1.用双指针来做,i开始指向最左端,j指向最右端。
2.然后移动 i 或者 j
3.左移或者右移动,容器底部长度都会减1,我们尽量保留比较高的边,移动边小的那一端,
因为保留较高那条边更容易出最大值。
class Solution {
//找最后一个大于它的位置,和第一个它小于的位置。
public int maxArea(int[] height) {
int i=0;
int j=height.length-1;
int maxSpacity=0;
//左移或者右移动,容器底部长度都会减1,我们尽量保留比较高的边,移动边小的那一端,更容易出最大值。
while(j>i)
{
int num1=Math.min(height[i],height[j])*(j-i);
maxSpacity=Math.max(num1,maxSpacity);
int num2=height[i];
int num3=height[j];
if(num2>num3)
{
j--;
}else{
i++;
}
}
return maxSpacity;
}
}