【新版】系统架构设计师 - 数学与经济管理

个人总结，仅供参考，欢迎加好友一起讨论

架构 - 数学与经济管理

考点摘要

• 最小生成树（★★）
• 最短路径（★）
• 网络与最大流量（★）
• 线性规划（★★★）
• 动态规划（★★）
• 预测与决策（★★★）
• 随机函数（★）
• 数学建模（★）

最小生成树

典型例题：

解析：

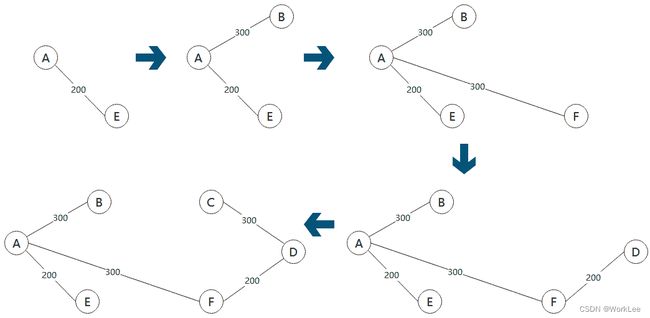
普里姆算法（以任意点开始，找这些点与其它点的最短距离）

1 任取一点，例如A。点A与其它各点中的最小距离为AE=200，将边AE以及点E纳入到已完成部分。

2 以点A、E与其他各点B、C、D、F这两个集合之间的最段距离为AB=AF=300，选边AB与点B纳入到已完成部分。

（备注：或边AF与点F也可以）

3 点A、B、E与点C、D、F两个集合的最短距离为AF=BF=300，将边AF（或边BF）与点F纳入已完成部分。

4 点A、B、E、F与点C、D两个集合之间的最段距离为FD=200，将边FD与点D纳入已完成部分。

5 点A、B、E、F、D与点C两个集合之间的最短距离为CD=300，将边CD与点C纳入已完成部分。

最终，所有6个点都已经接通，其选为AE、AB、AF、FD、CD，总长度为1300。

注：可以在第2部选择AF，第3部选择BF。

克鲁斯卡尔算法（此次找最短距离的边）

依次选取长度最短的边，题图中是6个结点则需要5条边（边数 = 结点数 - 1）

因此有：AE、FD为200，AB、BF、AF、CD为400，所以最终方案有3种。

综上所述，用哪个方法都可以，个人认为“普里姆算法”更好理解和操作。

典型例题：

解析：

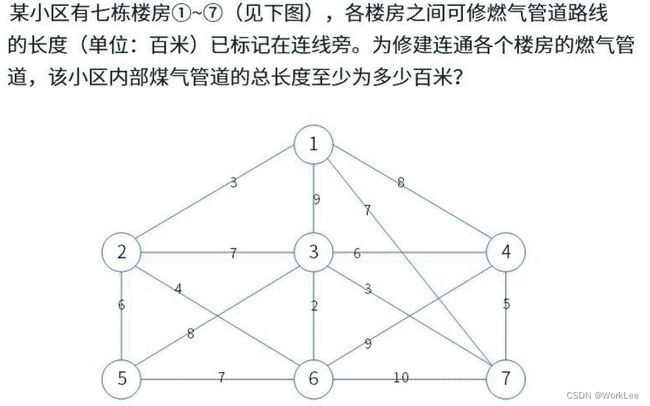
1 利用普里姆算法，找任意一点，假设从②开始，以②为基础②①距离最短，②① = 3。

2 以①②为基础，②⑥距离最短，②⑥ = 4。

3 以①②⑥为基础，⑥③距离最短，⑥③ = 2。

4 以①②③⑥为基础，③⑦距离最短，③⑦ = 3。

5 以①②③⑥⑦为基础，⑦④距离最短，⑦④ = 5。

6 以①②③④⑥⑦为基础，②⑤距离最短，②⑤ = 6。

7 至此，每个点都有连接，最终最短路径是：3 + 4 + 2 + 3 + 5 + 6 = 23。

最短路径

典型例题：

思路：

用Dijkstra（迪杰斯特拉）算法可以求网络中从源点到其他任何一个节点的最短路径。Dijkstra算法用U_i表示从源点1到节点i的最短距离，定义d_ij为弧(i，j)的长度，那么算法根据这两个量可以立即给出节点j的标号：

[U_j , i] = [U_i + d_ij , i]，d_ij >= 0，开始的节点的标号为[0，—]，表示该节点为源点。

解析：

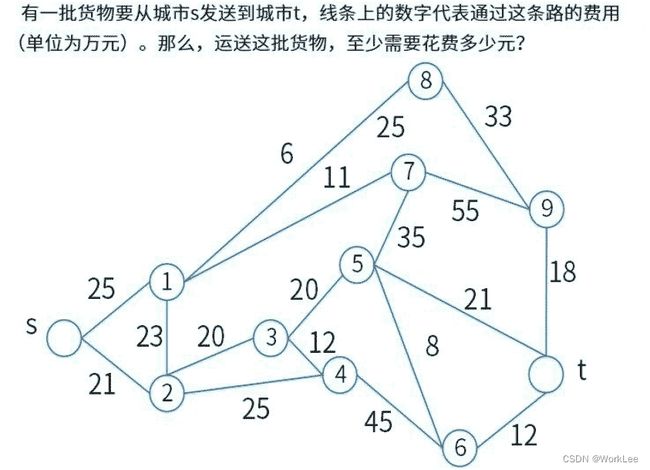
开始的节点的标号为[0，-]，表示该节点为源点。过程如下：

⑥节点，从④和⑤节点同时汇入，从④节点汇入是得到：[91，4]，⑤节点汇入是得到：[69，5]

所以按照最短路径，选择[69，5]为准，此时⑥节点为[69，5]

最终t阶段，可以从⑤、⑥和⑨节点同时汇入，那么

从⑤节点汇入是得到：[82，5]，从⑥节点汇入是得到：[81，6]，⑨节点汇入是得到：[82，9]

最终最短路径为81。

网络与最大流量

典型例题：

思路：

求最大流量，只需要找寻能同行的路线，减掉路线上最小流量，直到起点和结束没有任何路线位置，将减去的流量相加即可。

解析：

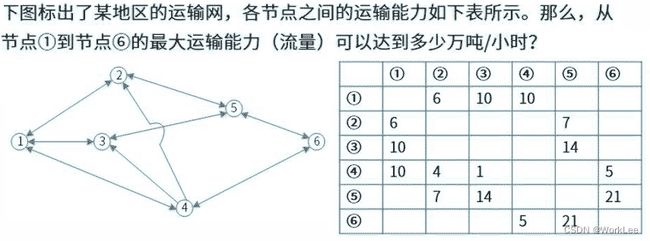
1 先按照题目要求把各个线路上标记上流量，如下：

2 ①到⑥，可以随便找任意一条路线，比如路线①②⑤⑥，路线上最小是①②，各路线 - 6，①②变0抹掉，如下：

3 路线①③⑤⑥，路线上最小是①③，各路线 - 10，①③变0抹掉，如下：

路线①④⑥，路线上最小是④⑥，各路线 - 5，④⑥变0抹掉，如下：

路线①④③⑤⑥，路线上最小是④③，各路线 - 1，④③变0抹掉，如下：

路线①④②⑤⑥，路线上最小是②⑤，各路线 - 1，②⑤变0抹掉，如下：

到这种没有任何路线①到⑥相通的情况，将之前减去的路线流量相加，最大流量是：6 + 10 + 5 + 1 + 1 = 23。

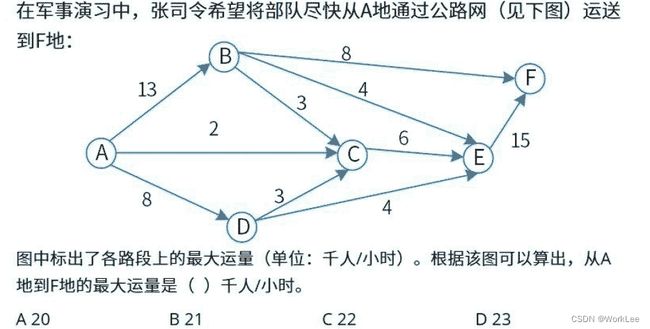
典型例题：

解析：

1 根据“找寻任何可行路线，减掉路线上最小流量”的思路，A到F有各种路线，随机找一条可行路线即可。

2 假设路线ABF，路线ABF只能减去8，AB等于5，然后BF等于0抹去。

3 路线路线ACEF，路线ACEF只能减去2，CE等于4，EF等于13，AC等于0抹去。

4 路线路线ADEF，路线ADEF只能减去4，AD等于4，EF等于9，DE等于0抹去。

5 路线路线ABEF，路线ABEF只能减去4，AB等于1，EF等于5，BE等于0抹去。

6 路线路线ADCEF，路线ADCEF只能减去3，AD等于1，CE等于1，EF等于2，DC等于0抹去。

7 最后，路线路线ABCEF，路线ABCEF只能减去1，BC等于1，EF等于1，AB等于0抹去，CE等于0抹去。

8 最终，没有路线再连接A和F，将减去的数相加最大运量为：8 + 2 + 4 + 4 + 3 + 1 = 22。

线性规划

在一组约束条件下来寻找目标函数的极值（极大值和极小值）问题。

线性规划问题的数学模型通常由线性目标函数、线性约束条件、变量非负条件组成（实际问题中的变量一般都是非负的）。

线性规划问题就是面向实际应用，求解一组非负变量，使其满足给定的一组线性约束条件，并使某个线性目标函数达到极值。满足这些约束条件的非负变量组的集合称为可行解域。可行解域中使目标函数达到极值的解称为最优解。

线性规划问题的最优解要么是0个（没有），要么是唯一的（1个），要么有无穷个（只要有2个，就会有无穷个）。

在实际应用中，可以直接求约束条件方程组的解，即是交叉点，将这些解代入到目标函数中判断是否极值即可。

典型例题：

思路：

线性规划最常用是列方程式，求最合理的即可。

解析：

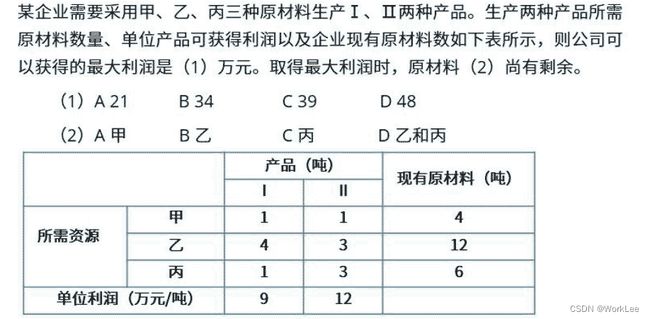
设生产Ⅰ的数量为 x ，生成Ⅱ的数量为 y，有如下方程式：

$\{\begin{array}{l}①x+y<=4\\ ②4x+3y<=12\\ ③x+3y<=6\end{array}$

①与②求得：x = 0，y = 4。验证③：x + 3y = 12，不合理

①与③求得：x = 3，y = 1。验证②：4x + 3y = 15，不合理

②与③求得：x = 2，y = 4/3。验证①：x + y = 10/3，合理

按照最大MAX = 9x + 12y，综上计算：x = 2，y = 4/3 为正确符合题目要求的解，最后：9 * 2 + 12 * (4/3) = 34

第2问，因为②与③求得合理解，那么①的最后计算值是小于4的，所以“甲”有剩余

动态规划

典型例题：

思路：

暴力求解，穷举法，枚举法

解析：

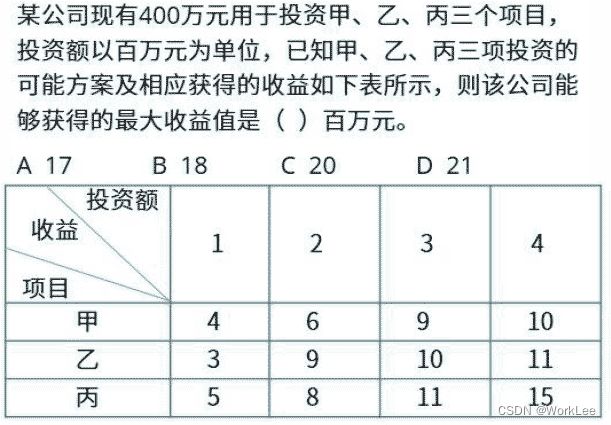
穷举法的意思，就是把所有的投资可能全部列出，算出所有可能的结果，如下：

从上面的表格中就可以清晰看出最大围18，也就是：甲投资1，乙投资2，丙投资1。

典型例题：

思路：

分配问题用贪心策略分析法，也就是先找出每行最小，全行减去最小（必要时找列的最小），也就是获取更多的“0”（同一行同一列有0）。

解析：

分别找出甲、乙、丙、丁每行最小值，然后全行减去这个最小值，如下：

这样就会发现甲和乙的C都为0的情况，这时我们按照列找A、B、C、D每列的最小值，全列减去最小值，如下：

此时，可以看到每行每列多有“0”存在，这是我们需要的状态，将行和列的“0”用直线连接起来，如下：

最后，寻找连线上，不在行和列直线交叉点上行的“0”，即可获得结果：甲在D，乙在C，丙在B，丁在A。

假设如果存在如，丙的B和D都是0情况，那么我们需要回到题目最初的表格，查看丙在B上用时会更少。

算工时：3 + 3 + 4 + 4 = 14；也可以把减去的值进行相加：2 + 3 + 4 + 4 + 1 = 14。

典型例题：

思路：

实例分解为更小的、相似的子问题，按照要求比对子问题之间的最优化解。

解析：

按照解题思路，需要拿到相似的子问题即可，那就按照单位运输利润为基础，如下：

由表数据可知，D单位利润最大，可以装2件8吨。

剩余2吨选择可以选择利润第二大的A，装2件，此时最大利润538元。

预测 - 博弈论

典型例题：

解析：

这种题目，需要用到数学中的矩阵求解，上图图中，囚徒A纵向分析，囚徒B横向分析。

思考方式，需要进行独立的思考，因为囚徒A并不知道囚徒B的想法，反过来同理。

假设囚徒B坦白，把囚徒B坦白当做已知条件，得到下面矩阵：

$$囚徒A=\left[\begin{array}{c}A坦白\to B坦白\\ A抵赖\to B坦白\end{array}\right]=\left[\begin{array}{c}-8\\ -10\end{array}\right]$$

如上，按照上面矩阵得知，囚徒A会选坦白，坐牢8年。

再假设囚徒B抵赖，把囚徒B抵赖当做已知条件，得到下面矩阵：

$$囚徒A=\left[\begin{array}{c}A坦白\to B抵赖\\ A抵赖\to B抵赖\end{array}\right]=\left[\begin{array}{c}0\\ -1\end{array}\right]$$

如上，按照上面矩阵得知，囚徒A会选坦白，无需坐牢。

最终，囚徒A会选坦白，更合适。

同理，假设囚徒A坦白，把囚徒A坦白当做已知条件，得到下面矩阵：

$$囚徒B=\left[\begin{array}{c}B坦白\to A坦白\\ B抵赖\to A坦白\end{array}\right]=\left[\begin{array}{c}-8\\ -10\end{array}\right]$$

如上，按照上面矩阵得知，囚徒B会选坦白，坐牢8年。

再假设囚徒A抵赖，把囚徒A抵赖当做已知条件，得到下面矩阵：

$$囚徒B=\left[\begin{array}{c}B坦白\to A抵赖\\ B抵赖\to A抵赖\end{array}\right]=\left[\begin{array}{c}0\\ -1\end{array}\right]$$

如上，按照上面矩阵得知，囚徒B会选坦白，无需坐牢。

最终，囚徒B会选坦白，更合适。

综上，最终囚徒A和囚徒B都选择坦白，结果的都判8年坐牢。

预测 - 状态转移矩阵

典型例题：

解析：

题目给定的是当月与下月的占有率变化，但是要求2个月后的结果，所以需要计算两个月的数据。

题中给定矩阵，根据矩阵Am*n × Bn*p = Cm*p，前者的列n和后者的行n相同才可以。

题目已给定当月的占有率，即：(0.5，0.5)，也就是1行2列，用它去和矩阵P就行相乘

按照公式：1行2列 × 2行1列，也就是：0.5 * 0.8 + 0.5 * 0.4 = 0.6，这是矩阵第一个数

再根据公式：0.5 * 0.2 + 0.5 * 0.6 = 0.4，这是矩阵第二个数

也就是，下月的A和B市场占有率是：(0.6，0.4)

再下一个月（第2个月）的计算方式同上，但是需要用占有率：(0.6，0.4) 进行计算

0.6 * 0.8 + 0.4 * 0.4 = 0.64，0.6 * 0.2 + 0.4 * 0.6 = 0.36

所以，2个月后的A和B市场占有率是：(0.64，0.36)

(0.5，0.5) ==>>> (0.64，0.36)，故选C

典型例题：

解析：

和上面的题相似，假设Z = (Z1，Z2)，且Z1 >= 0，Z2 >= 0，Z1 + Z2 = 1

题目给出公式要求：ZP = Z，得如下：

也就是：Z1 * 0.8 + Z2 * 0.4 = Z1，Z1 * 0.2 + Z2 * 0.6 = Z2

可以计算得：2 * Z2 = Z1，因为Z1 + Z2 = 1，所以：Z1 = 2/3，Z2 = 1/3。

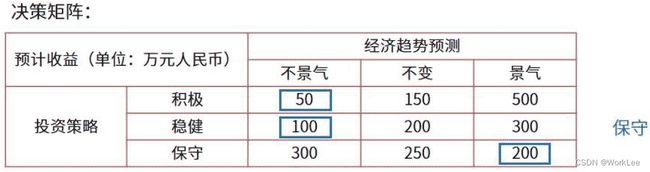
决策 - 不确定型决策

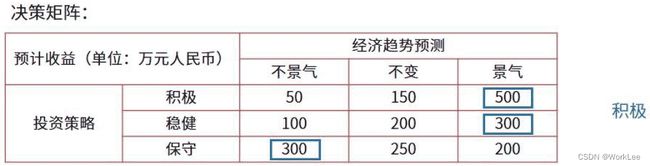
乐观主义（积极的）

乐观，积极，有赚钱的，好的，好收益的，等各种积极的字眼都为乐观主义。

总结：先在各个方案中选最大的那个状态，然后这些最大的状态里再选最大的那个。

悲观主义（保守的）

悲观，不赚钱的，不积极的，收益最不好的，赔钱的，等各种负面的字眼都为悲观主义。

总结：先在各个方案中选最小的那个状态，然后这些最小的状态里再选最大的那个。

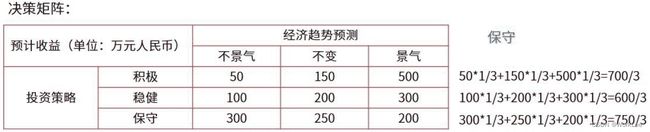
等可能

总结：每种状态概率乘以数据之和，在这些概率和中取最大的那个。

后悔值

总结：先在各个方案中，

1. 如果是要求是收益状态，每个方案里面选最大的那个状态，然后用它去减得差，得到后悔值矩阵。
2. 如果是要求是损失状态，每个方案里面选最小的那个状态，然后用它去减得差，得到后悔值矩阵。
3. 然后在这个后悔值矩阵里，每个方案里再选最大的那个后悔值矩阵，然后选里面最小那个。

决策 - 决策树

典型例题：

解析：

水路：7000 * 3/4 + ( 7000 + 90000 * 10% ) * 1/4 = 9250元

陆路：10000元

典型例题：

解析：

系统A：95 * 35% + 70 * 40% + 85 * 25% = 82.5

系统B：75 * 35% + 95 * 40% + 90 * 25% = 86.75，选B

典型例题：

解析：

自行开发：0.3 * 38 + 0.7 * 45 = 42.9

复用：0.4 * 27.5 + (0.6 * 0.2 * 31 + 0.6 * 0.8 * 49) = 38.24

购买：0.7 * 21 + 0.3 * 30 = 23.7

承包：0.6 * 35 + 0.4 * 50 = 41

故选A

典型例题：

解析：

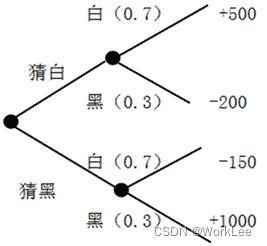
画出策略树，如下图：

如果选白球的：0.7 * 500 + 0.3 * (-200) = 290

如果选黑球的：0.3 * 1000 + 0.7 * (-150) = 195

故，选白球猜合适

另外：

设出现白球的概率为P：

P * 500 + (1 - P) * (-200) = (1 - P) * 1000 + P * (-150)

计算得到的这个P叫白球的转折率（P = 0.65）

排队论

典型例题：

解析：

设8点前已排队等候的人数为m，每分钟可以来x人，每个入口每分钟能进y人

①：8个入口 * 60分钟 * y = 60 * x + m ==>> 8 * 60 * y = 60 * x + m

②：10个入口 * 40分钟 * y = 40 * x + m ==>> 10 * 40 * y = 40 * x + m

① - ②消除x得：80y = 20x ==>> ③：4y = x

③带入①得：m = 240y

所以要20分钟消除排队现象有：n个入口 * 20分钟 * y = 20分钟 * 4y + 240y，求得：n = 16

依据4y = x，所以8:00应开入口16个，而8:20由于消除了排队，开口数量只需要4个就行了。

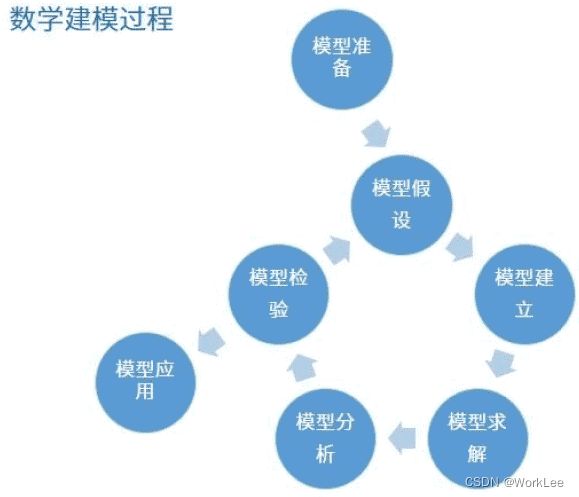
数学建模

数学建模是一种数学的思考方法，是运用数学的语言和方法，通过抽象和简化，建立能近似刻画并解决实际问题的模型的一种强有力的数学手段。

• 模型准备：了解问题的实际背景，明确其实际意义，掌握对象的各种信息。用数学语言来描述问题。
• 模型假设：根据实际对象的特征和建模的目的，对问题进行必要的简化，并用精确的语言提出一些恰当的假设。
• 模型建立：在假设的基础上，利用适当的数学工具来刻画各变量之间的数学关系，建立相应的数学结构。只要能够把问题描述清楚，尽量使用简单的数学工具。
• 模型求解：利用获取的数据资料，对模型的所有参数做出计算(估计）。
• 模型分析：对所得的结果进行数学上的分析。
• 模型检验：将模型分析结果与实际情形进行比较，以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合，则要对计算结果给出其实际含义，并进行解释。如果模型与实际吻合较差，则应该修改假设，再次重复建模过程。
• 模型应用：应用方式因问题的性质和建模的目的而异。
  

数学建模 - 模型分析

• 模型的合理性分析（最佳、适中、满意等）
• 模型的误差分析（模型误差、观测误差、截断误差、舍入误差、过失误差、绝对误差、相对误差等）
• 参数的灵敏性分析（变量数据是否敏感，在最优方案不变的条件下这些变量允许变化的范围）

数学建模 - 模型校验

• 利用实际案例数据对模型进行检验是很常见的。将模型作为一个黑盒，通过案例数据的输入，检查其输出是否合理。这是应用人员常用的方法。
• 可以请专家来分析模型是否合理。经验丰富的专家一般会根据模型自身的逻辑,再结合实际情况，分析是否会出现矛盾或问题。
• 利用计算机来模拟实际问题，再在计算机上检验该数学模型。有时很难用实际案例或聘请专家来检验模型,例如，试验或实验的代价太大，难以取得实际案例，有的项目技术比较新，缺乏有经验的专家。例如，对某种核辐射防护建立的数学模型，采用计算机模拟方法来检验就十分有效。

数学建模 - 例题

解析：C

解析：D