什么是图?
第一章 什么是图?
什么是图?
定义: 图是由若干的顶点(即点或节点)及连接两顶点的边(或线或关系)所构成的图形。
原文: A graph in this context is made up of vertices (also called nodes or points) which are connected by edges (also called links or lines).
引用: https://en.wikipedia.org/wiki/Graph_theory
在看到上述定义我们应该还是一脸的疑惑,因为我们不知道其前后关系。只知晓一个定义,这样的知识其实是很容易忘记的,那让我们开始完整学习吧。
一、导论
在我们先今,数据直接的关联在不断增强,系统也越发复杂庞大。我们怎么把数据之间的关联利用好,变得越发的重要。
1.1错误的”图”
在我们未接触或者了解图的时候,我们眼中的图是这样的
上述其实就是我们生活中接触到的”图像”和”图表”,这些并不是我们今天要将的主题的”图”。
那图张什么样子呢?
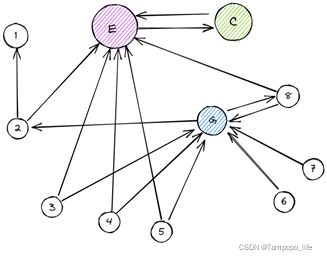
上述应该是一个比较经典的图结构,这个图是PageRank 这个图算法具有代表性的案例关于PageRank图算法本次不做介绍,大家可以自行百度相关内容。
上图中各个圈(1、2、3、E、C、G等等)即开篇-图定义中的顶点(即点或节点),图连接各个圈的线即开篇-图定义中边(或线或关系)。通过上述内容我们大致了解了什么图?但图的起源、图的发展、图的作用、图的分类、以及图现在的趋势我们是不了解的,让我继续下面的内容吧。
1.2图的起源
其实图的发展历史可以追溯到1937年,当时遇到一个问题,即知名的”哥尼斯堡七桥”问题。当时有一个人欧拉,他解决了这个问题,并且他的解决方案奠定了我们现在所说的图论。
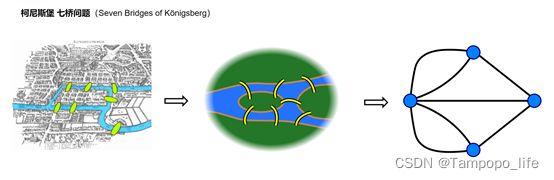
问题是这样的: 如何将下图中的各个桥只走一次,并且全部走完呢?
上图为哥尼斯堡市,图中的绿色为连接城镇的桥梁,问题就是如何将图中的绿色每个只走一次,并且全部走完。
在1737年的时候欧拉解决了该问题,通过将桥和地方进行抽象将点和边。通过”一笔画”方法解决了该问题。(一笔画这边不做展开,感兴趣的自行搜索相关资料),这简单4点7边奠定了我们现在使用的”图论”。
我们上述不断的在说图论,那么图论和我们讲说的图是什么关系?
图论是以图作为研究对象。图论是离散数学的一个分支,是一门研究图(Graph)的学问。所以我们常说的图其实就是图论研究的对象而已。
我们常将图做如下表示:
Graph即图对象有时也写为G,V为顶点集合,E为边集合
1.3 图的分类
我们日常工作中会接触到很多所谓的图,有各种各样的类别,知道这些图的类别是我们和其人沟通重要的知识点之一。
图有很多划分的标准,下面我们举例常见的几个。
1.根据点边类型的数量进行划分。
① 同构图: 一种点类型一种边类型的图
② 异构图: 不同类型的节点和边的图
2.根据图的联通情况、方向、属性、环路我们可以在进行划分
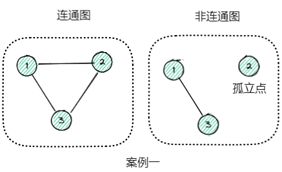
③ 连通图:
根据点是否与其他点相连,我们将其划分为连通图和非连通图。通过连通情况我们可以评估这个图的关系情况,是否存在很多“孤岛”甚至是孤立点的情况。
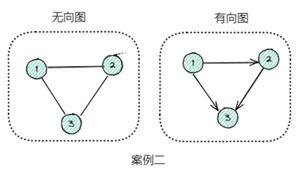
④ 有向图 :
根据边上是否存在方向,我们将图划分为有向图和无向图。有向和无向作用与不同的业务场景,当例如我们表达伙伴关系时,我们的方向是无向,因为彼此只有连接没有谁对谁的概念。当我们表达关注关系时,谁关注谁这时候是有向的。
⑤ 有环图:
根据图中是否存在环路,我们将其划分为有环图和无环图。存在环的图即从自身出发沿方向可以回到自身。环路的判断在金融场景中非常有用。
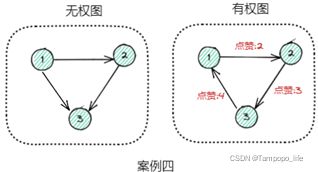
⑥ 带权图:
根据边上是否存在属性,我们将其划分为无权图和有权图或者叫带权图。在我们实际的生成环境中,属性图必不可少的,无带属性的图往往过于简单,并不符合实际的业务场景。
3.根据图的拓扑结构我们在进行划分
⑦ 随机结构:
均匀分布,没有结构或者层级模式。任何顶点到其他顶点都是等概率的。
⑧ 小世界结构:
该结构在社交网络中非常常见也非常具有代表性,其基于“6度空间理论”,你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过6个中间人你就能够认识任何一个陌生人。
⑨ 无标度结构
图中符合幂律分布,就会产生无标度网络比较有代表性的为万维网。
4.根据点边数量以及连接关系划分
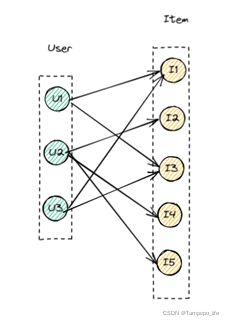
⑩ 二部图(又叫”二分部”)
下图中User和Item同类型之间不关联,两种之间相互连接。即为二部图,将其衍生可以到K-部图。
1.4 图的使用场景
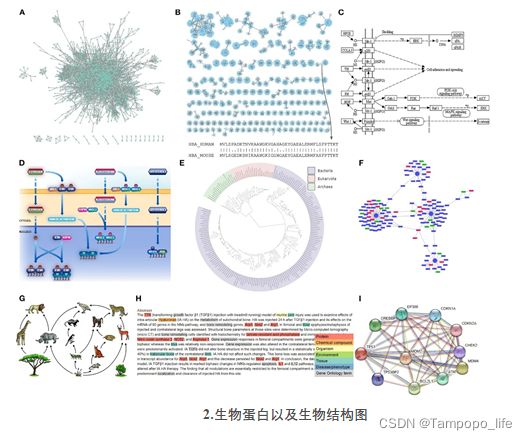
其实现在图已经融入了我们生活中的方方面面,例如我们衣食住行中用到的美团,他们就用了图进行推荐。在金融场景中图技术已经被大量金融机构用于欺诈检测、团伙发现等各个业务场景中。图的大到可以评估在一个大型系统的运行机制。小到可以衡量生物蛋白之间的稳定性。图已无处不在,并且万物皆可图进行表示。
1.5 什么是图算法
我们在使用图当中经常会用到图算法这个技术,那什么是图算法,图算法到底是做什么的呢?其实:图算法是图分析工具。图分析使用图的方法来分析关联数据的过。图算法是分析关联数据的一种有效方法。因为图的数学运算是针对关联运算进行设计的。图算法基于图论的数学原理,图算法利用顶点之间的关系来推断复杂系统的组织形式和动态性。使用者可以利用这些算法来发现隐藏的信息,关联甚至可以做到预测。那目前有些图算法呢?能介绍一下吗?
目前图算法主要的分类如下:
- 一、Centrality
- PageRank
- Degree Centrality
- Closeness Centrality
- Betweenness Centrality
- 二、Community detection
- Louvain
- Label Propagation
- Local Clustering Coefficient
- Weakly Connected Components
- 三、Path finding
- Random Walk
- Shortest Path
目前上述三类为常用的,这里只列出较为常用得一些算法具体就不在本处展开了。上述图算法分类主要是来自neo4j,wiki直接采用了字母进行分类,后续笔者如果找到背后的分类逻辑会告知大家。当然图算法还有很多其他分类,比如Similarity、Node embeddings、甚至图神经网络。图神经网络自2018年开始在顶会论文中崭露头角,后其影响力变得日益明显。虽然现阶段图神经网络现在还存在很多弊端,但是也不能遮盖其光芒。
以下为参考引用希望对你们有帮助:
https://en.wikipedia.org/wiki/List_of_algorithms#Graph_algorithms
1.6 图的发展趋势
讲了这么多,好像“图”很牛逼啊。为什么我之前都没有听过说它呢。其实一个新生事物得发展需要一定阶段的时间沉底才会呈现出来。图现在就处于这个趋势中。从下面图数据库的发展趋势我们就可以看出其潜力。
万物皆可用图表示,我们在使用数据库的中经常用E-R图确定连接关系,基于此基础,规定各种范式,在进行表的设计最后存储。那么为什么不能直接通过E-R的关联,以关联进行存储呢?我们的连表查询是不是在图数据库中就是一个非常简单的遍历呢? 故为什么我们不采用图来存储?当然一个技术的选型需要很多决策,考虑的因素也不可能像我所说的那么简单。但希望所说的对读者有所帮助。