Python3数据分析与挖掘建模（10）复合分析-交叉分析与实现示例

1. 复合分析

1.1 概述

复合分析（Factorial Analysis）是一种统计分析方法，用于研究多个因素对观测结果的影响，并探究各个因素之间的相互作用效应。

在复合分析中，研究者会选择多个因素（也称为处理变量或独立变量），并对这些因素的不同水平进行组合。每个因素的水平表示该因素所具有的不同取值或条件。通过对不同因素水平的组合进行实验或观测，研究者可以探索这些因素对结果变量（也称为因变量）的影响。

复合分析可以帮助研究者了解以下方面：

1. 主效应（Main Effects）：即每个因素对结果变量的独立影响。通过比较不同因素水平的组合，可以确定每个因素对结果的影响程度。

2. 交互效应（Interaction Effects）：即多个因素之间的相互作用对结果的影响。交互效应表示多个因素同时存在时，它们之间是否存在非加性的影响，即相互作用效应。

复合分析可以应用于各种领域和实验设计，例如生物学、心理学、社会科学等。研究者可以利用复合分析来确定最佳因素组合、解释因素之间的相互作用以及预测结果变量在不同条件下的表现。

在实施复合分析时，常用的统计方法包括方差分析（ANOVA）、线性回归模型、混合效应模型等。这些方法可以帮助研究者对复合分析的数据进行建模和推断，以得出结论和进行预测。

总而言之，复合分析是一种多因素的统计分析方法，用于研究多个因素对观测结果的影响，并探索因素之间的相互作用效应。它可以提供对因素影响和相互作用的深入理解，以支持科学研究和决策制定。

1.2 交叉分析

交叉分析（Cross-Tabulation Analysis）： 交叉分析是一种统计分析方法，用于研究两个或多个变量之间的关系。它通过将数据按照不同变量的不同取值进行分组，并计算各组之间的频数或比例，从而揭示变量之间的相关性或差异。交叉分析常用于描述分类变量之间的关系，例如性别与购买偏好、地区与产品偏好等。

1.3 因子分析

因子分析（Factor Analysis）： 因子分析是一种统计方法，用于探索多个观测变量之间的潜在结构或维度。它通过分析观测变量之间的协方差矩阵，将这些变量归纳为较少的因子或维度，以解释变量之间的共同方差。因子分析可用于数据降维、变量分类和构建潜在变量模型。

1.4分组与钻研

分组与钻研（Segmentation and Drilling）： 分组与钻研是一种数据分析方法，用于将数据按照特定的标准或属性进行分组，并对各组进行深入研究。通过分组与钻研，可以识别出不同组之间的差异和相似性，发现隐藏在数据中的模式和洞察，并为不同组别制定针对性的策略或决策。

1.5聚类分析

聚类分析（Cluster Analysis）： 聚类分析是一种无监督学习方法，用于将相似的个体或对象归类到同一组别中。聚类分析通过测量个体之间的相似性或距离，并将相似的个体划分为不同的簇或群组。聚类分析可用于发现数据中的群集结构、识别潜在的子群体或细分市场，并支持个性化营销、客户分类和产品定位等领域。

1.6 相关分析

相关分析（Correlation Analysis）： 相关分析是一种统计方法，用于衡量两个或多个变量之间的相关性或关联程度。它通过计算变量之间的相关系数（如皮尔逊相关系数）来评估它们之间的线性关系。相关分析可以帮助研究者确定变量之间的正向或负向关系，从而理解它们之间的相互依赖性或影响关系。

2. 交叉分析-独立t检验

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ss
import seaborn as sns

# 读取 HR.csv 文件并存储为 DataFrame
df = pd.read_csv("../data/HR.csv")

# 按部门分组并获取索引
dp_indices = df.groupby(by="department").indices

# 获取销售部门和技术部门的离职情况值
sales_values = df["left"].iloc[dp_indices['sales']].values
technical_values = df["left"].iloc[dp_indices['technical']].values

# 执行 t 检验并打印 p 值
t_statistic, p_value = ss.ttest_ind(sales_values, technical_values)
print(p_value)

# 获取部门名称列表
dp_keys = list(dp_indices.keys())

# 创建用于存储 t 值的矩阵
dp_t_mat = np.zeros([len(dp_keys), len(dp_keys)])

# 创建一个新的图形对象
plt.figure()

# 遍历部门名称列表，计算 t 值并填充矩阵
for i in range(len(dp_keys)):
    for j in range(len(dp_keys)):
        # 执行 t 检验并获取 p 值
        p_value = ss.ttest_ind(df["left"].iloc[dp_indices[dp_keys[i]]].values,
                               df["left"].iloc[dp_indices[dp_keys[j]]].values)[1]
        if p_value < 0.05:
            dp_t_mat[i][j] = -1  # 如果 p 值小于 0.05，则将 t 值设置为 -1，表示显著差异
        else:
            dp_t_mat[i][j] = p_value

# 绘制热力图并设置部门名称标签
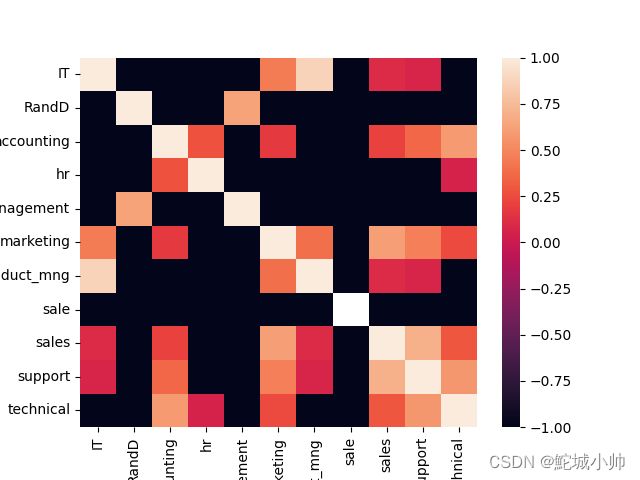
sns.heatmap(dp_t_mat, xticklabels=dp_keys, yticklabels=dp_keys)

# 显示图形
plt.show()

该代码的功能是对 HR 数据集中的部门进行交叉分析。主要步骤如下：

1. 导入所需的库：pandas、numpy、matplotlib、scipy.stats 和 seaborn。

2. 读取 HR.csv 文件并将其存储为 DataFrame。

3. 使用 groupby 方法对数据按部门进行分组，并获取各个部门的索引。

4. 从 DataFrame 中提取销售部门和技术部门的离职情况值。

5. 使用 ss.ttest_ind 函数执行 t 检验，比较销售部门和技术部门的离职情况，并打印出 p 值。

6. 创建一个矩阵来存储各个部门之间的 t 值。

7. 创建一个新的图形对象。

8. 使用嵌套循环计算每对部门之间的 t 值，并将结果填充到矩阵中。如果 p 值小于 0.05，则将 t 值设为 -1，表示存在显著差异。

9. 使用 seaborn 库的 heatmap 函数绘制热力图，显示部门之间的 t 值

分析的图示：

 

交叉分析结果的热图中，黑色部分表示离职率存在显著差异的部门对，而红色部分表示离职率没有显著差异的部门对。

具体来说，黑色部分代表的部门对（如IT与technical）在离职情况上存在相关影响，即这两个部门的离职情况之间有显著差异，可能是由于工作性质、工作环境或其他因素导致的。

而红色部分代表的部门对（如hr与technical）在离职情况上没有显著差异，即这两个部门的离职情况之间的差异不具有统计学上的显著性，可能是因为这两个部门的工作性质、员工群体或其他因素相似，导致离职情况相对一致。

通过观察交叉分析结果的热图，可以更直观地了解不同部门之间的离职情况差异，并对可能存在的相关影响进行初步分析和解释。

3. 交叉分析-透视表

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 读取HR.csv数据文件，并将其存储在DataFrame对象df中
df = pd.read_csv("../data/HR.csv")

# 使用pd.pivot_table()函数创建透视表，计算"left"列的均值，按照"promotion_last_5years"和"salary"作为行索引，
# "Work_accident"作为列索引，np.mean作为聚合函数
piv_tb = pd.pivot_table(df, values="left", index=["promotion_last_5years", "salary"], \
                        columns=["Work_accident"], aggfunc=np.mean)

# 打印透视表piv_tb
print(piv_tb)

# 使用seaborn库的heatmap函数绘制热图，将透视表piv_tb作为数据，设定颜色映射为"Reds"，颜色范围为0到1
sns.heatmap(piv_tb, vmin=0, vmax=1, cmap=sns.color_palette("Reds", n_colors=256))

# 显示图形
plt.show()

在上述代码中，我们首先使用pd.read_csv()函数读取HR.csv数据文件，并将其存储在DataFrame对象df中。然后，使用pd.pivot_table()函数创建透视表piv_tb，计算"left"列的均值，并按照"promotion_last_5years"和"salary"作为行索引，"Work_accident"作为列索引。

接下来，我们使用seaborn库的heatmap()函数绘制热图，将透视表piv_tb作为数据，设定颜色映射为"Reds"，并将颜色范围设置为0到1。最后，使用plt.show()显示图形。热图将展示不同组合条件下"left"列的均值，并以颜色的深浅表示不同的数值。

如下图：