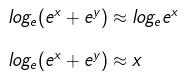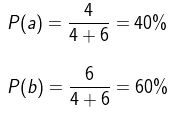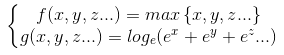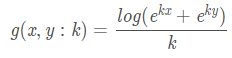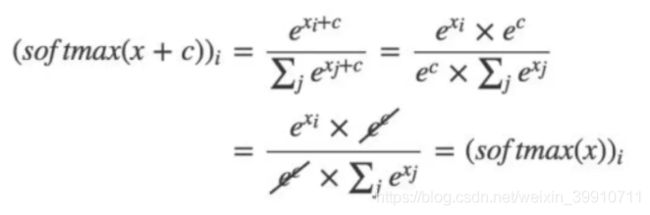SoftMax函数

目录

1 Softmax的形式

 2 hardmax的特性     

3 softmax和hardmax的相似性

4 softmax函数概率模型构建

5 softmax函数优化

---

1 Softmax的形式

       Softmax函数是在机器学习中经常出现的，时常出现在输出层中。

       softmax的表达式：

               

      而下面我们要介绍的softmax“暂时”长相和它有些不一样，暂且叫做softmax_g：      

                         

       为什么叫softmax呢？根据CS224n的说法，主要是因为softmax函数的效果是能够让vector中最大的数被取到的概率非常大，同时又不至于像max函数那么极端使得取到其他数的概率为0，所以叫softmax。

 2 hardmax的特性     

        softmax函数其实是从hardmax演变而来的，hardmax函数其实是我们生活中很常见的一种函数，表达式是：            

                    

        表达的意思很清楚，从y和x中取较大的那个值，为了方便后续比较，我们将hardmax的形式换一下：

                                                                                 

         此时，函数本质功能没变，我们只是对定义域做了一个限制，即：

               

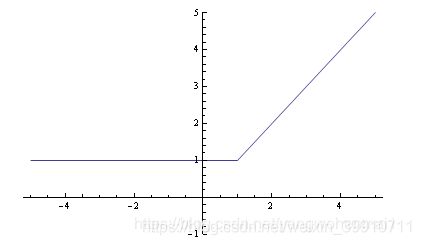
         其图形如下：

                

       很显然这个函数在 x = 1 处是连续不可导的，可导能帮我们做很多事，那我们有没有办法对他变形，找到一个连续可导的近似函数？

3 softmax和hardmax的相似性

        此时就有了softmax_g函数：

                

       指数函数有一个特点，就是变化率非常快。当x>y时，通过指数的放大作用，会使得二者差距进一步变大，即：

                

        所以有：

                 

       所以g(x，y)表达式有：

               

         因此根据上面的推导过程，g(x，y)约等于x，y中较大的值，即：

                 

        所以我们得出一个结论，g(x，y)是max{x，y}的近似函数，两个函数有相似的数学特性。我们再来看一下softmax_g函数的图像：

               

        很显然这是一个连续且处处可导的函数，这是一个非常重要的特性，g(x，y)即具有与max{x，y}的相似性，又避免了max{x，y}函数不可导的缺点。

         我们把两张图叠加到一起来看看，红色的折线是hardmax函数，他有一个尖尖的棱角，看起来很"hard"。蓝色的弧线看起来就平滑的多，不那么"hard"，这就是softmax_g函数了。这就时softmax_g函数名称的由来。

         从图上可以看出，当x，y的差别越大时，softmax_g和hardmax函数吻合度越高

                    

4 softmax函数概率模型构建

        那么回到最初的问题，这个softmax_g函数和我们神经网络里面做分类层的softmax函数有什么关系呢？

        假设我们要从a，b两个未知数字中取一个较大的值，即max{a，b}，那么取到两个数字的概率分别是多少呢？我们可以建立一个概率模型：

        1. 当a = b的时候，取a，b任意一个数字都可以，所以，取a或者取b的概率各50%。

                     

        2. 当a = 4，b = 6的时候，b比a更大，因此我们更倾向于取b，那么我们取到b的概率应该会更大一点

                                                                                                                                     

        3. 当a = 8，b = 2的时候，a比b更大，因此我们更倾向于取a，那么我们取到a的概率应该会更大一点

                                                                                                                                       

        当变量变多时，hardmax就变成了max{s1，s2，s3，s4，...sn}，此时根据我们假设的概率模型，取到每一个样本点的概率就是：

                     

         注：该公式中的为 max 函数中的参数。

        对于神经网络来说，训练的过程中处理损失调整权重矩阵的时候，需要用到求导。在第二部分我们已经了解到，hardmax函数并不是处处可导的，那么此时就用hardmax的近似函数softmax_g来代替他，我们已知二者表达式之间的关系：

                    

        因此，根据hardmax函数的表达式，仿照该公式，使用参数代替，带入，得出softmax的概率模型表达式：

                    

        soft maximum是hard maximum函数的近似，并且同hard一样是凸函数，它的方向变化是连续的、光滑的、可导的（敲黑板，这是重点），并且实际上是可以求任意阶导数的。这些性质使其在凸优化中具有良好的特性，事实上最早引入soft maximum就是在优化学科中（optimization）。

5 softmax函数优化

        注意到，soft maximum_g的近似程度实际上依赖于（两数之间的）scale（常翻译为尺度、这里应理解为比例、数量范围意思）。如果我们对 x,y 乘上比较大的一个常数，那么soft maximum_g将会更加接近hard maximum。例如g(1,2)=2.31 ，但是g(10,20)=20.00004 。所以我们可以设计一个hardness因子在soft maximum_g函数中。例如：

                  

        通过调节k，可以自由的让soft maximum_g逼近maximum。而且对任意给定k，soft maximum_g函数依然是可导的，但是其导数大小随着k的增加而增加，极限为无穷大，此时soft 收敛到hard maximum。

        虽然soft maximum_g的数学理论已经很清楚了，但是在实际计算中，还是会遇到一些问题，主要是因为计算机在进行浮点数计算的时候，存在overflow 和 underflow 问题，简而言之，就是计算的时候，前者太大，计算机认为是无穷大，后者太小，计算机直接等于零。所以带来一系列奇怪的问题。

        解决的方法也很简单，利用关系：

                 

        证明：

                   

        你会发现通过这样的手段，假如我们选取k为x,y中较大的数，即k = max {x,y} 。那么（4）中两项一个为0，一个为负数。自然就不会溢出了。

        虽然其中“ exp(minimum - maximum) ”依然可能下溢到0，但是此时不影响我们返回maximum值。实际上从等价计算式子也能看出soft maximum函数的一些特点，首先，其一定大于hard 的结果；其次，当x,y两个值差异比较大的时候，soft和hard的结果越接近。当x，y的值很接近的时候，soft和hard的值偏离程度变大，特别是当x,y相等，偏离最远，近似程度最差。

总结：

        在softmax函数对vector值进行计算，转换为[0, 1]区间的概率值的时候，往往会先对vector中每个元素减去一个max(vector)值。

        那么为什么要对每一个x减去一个max值呢？从需求上来说，如果x的值没有限制的情况下，当 x 线性增长，e 指数函数下的x 就呈现指数增长，一个较大的x（比如1000）就会导致程序的数值溢出，导致程序error。所以需求上来说，如果能够将所有的x 数值控制在 0 及 0 以下，则不会出现这样的情况，这也是为什么不用min而采用max的原因。

        数学上保证正确性：即正确性的关键就是要证明：softmax(x)=softmax(x+c)

         

        上面就是简单的数学推导过程，不难发现，对任意常数c来说，都不会影响softmax的结果。所以只要把常数c设置为-max就可以实现上面的优化效果。