解数独--难的一批
1题目
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例 1:
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
2链接
题目链接:37. 解数独 - 力扣(LeetCode)
视频链接:回溯算法二维递归?解数独不过如此!| LeetCode:37. 解数独_哔哩哔哩_bilibili
3解题思路
本题与N皇后问题不同的是,递归维度又高了一层。以前都是一维递归,本题是二维递归
N皇后问题 (opens new window)是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来遍历列,然后一行一列确定皇后的唯一位置。
本题就不一样了,本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
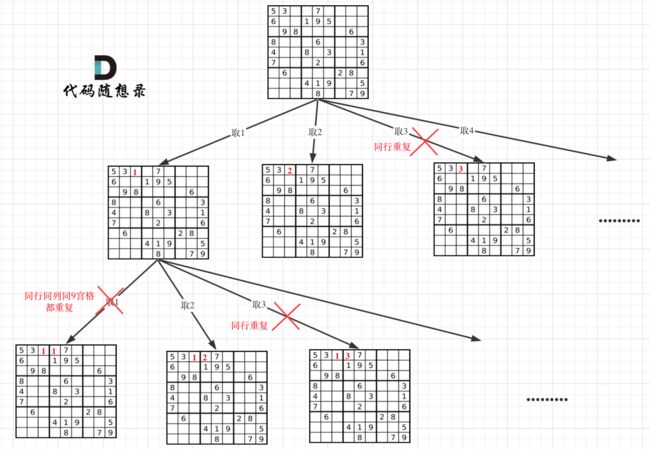
因为这个树形结构太大,抽取一部分,如图所示:
回溯三部曲
1、确定函数参数及返回值
递归函数的返回值需要是bool类型,为什么呢?
因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值。
bool backtracking(vector>& board) 2、确定递归终止条件
本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
不用终止条件会不会死循环?
递归的下一层的棋盘一定比上一层的棋盘多一个数,等数填满了棋盘自然就终止(填满当然好了,说明找到结果了),所以不需要终止条件!
那么有没有永远填不满的情况呢?
这个问题在递归单层搜索逻辑里再来讲!
3、单层递归逻辑
在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归)
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
bool backtracking(vector>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
if (isValid(i, j, k, board)) {
board[i][j] = k; // 放置k
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; // 回溯,撤销k
}
}
return false; // 9个数都试完了,都不行,那么就返回false
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
} 注意:if (backtracking(board)) return true; // 如果找到合适一组立刻返回。然后就不会再撤销填进去的数字k了,这样就保证了合法的数字k留在了棋盘之中。
注意这里return false的地方,这里放return false 是有讲究的。
因为如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解!
那么会直接返回, 这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去!
4、递归三部曲外番--判断棋盘合法性
判断棋盘是否合法有如下三个维度:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
bool isValid(int row, int col, char val, vector>& board) {
for (int i = 0; i < 9; i++) { // 判断行里是否重复
if (board[row][i] == val) {
return false;
}
}
for (int j = 0; j < 9; j++) { // 判断列里是否重复
if (board[j][col] == val) {
return false;
}
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) {
return false;
}
}
}
return true;
} 4代码
class Solution {
private:
bool isvalid(int row, int col, char val, vector>& board) {
for (int i = 0; i < 9; i++) { //判断当前行是否重复
if (board[row][i] == val) return false;
}
for (int j = 0; j < 9; j++) { //判断当前列是否重复
if (board[j][col] == val) return false;
}
int startRow = (row / 3) * 3; //通过去余的方式,重定位每个小九宫格的起始位置
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) {// 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val) return false;
}
}
return true;
}
bool backtracking(vector>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
if (board[i][j] == '.') { //遇到空格才继续往下判断是否可行
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
if (isvalid(i, j, k, board)) {
board[i][j] = k; //放置k
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; //回溯撤销k
}
}
return false; //九个数字都实验完了,均找不到一组解
}
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
public:
void solveSudoku(vector>& board) {
backtracking(board);
}
};