算法竞赛必考算法——动态规划(01背包和完全背包）

动态规划(一)

1.01背包问题

1.1题目介绍

1.2思路一介绍(二维数组)

代码如下：

#include
#include
using namespace std;
 const int N=1010;
 int v[N],w[N]; //v[N]是物品体积 w[N]是物品的价值
 int f[N][N]; //f[i][j]在体积不超j的前提下，从i个物品中选择最大值
 int main()
 {
     int n,m;
     cin>>n>>m;
     for(int i=1;i<=n;i++)
     {
         cin>>v[i]>>w[i];
     }
     for(int i=1;i<=n;i++)
     {
         for(int j=1;j<=m;j++)
         {
             f[i][j]=f[i-1][j];
             if(j>=v[i])//如果我们的背包容量j大于第i个物品的体积，我们在进行决策是否加入第i个物品
             f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
         }
     }
     cout<<f[n][m]<<endl;
     return 0;
 }

1.3思路二介绍(一维数组) 空间优化

  为什么可以使用一维数组？

  我们先来看一看01背包问题的状态转移方程，我们可以发现 f[i]只用到了f[i-1]，其他的是没有用到的，我们可以用滚动数组来做。
  还有一个原因就是我们在计算f[i] [j]的时候我们只用到了f[i-1] [j]和f[i-1] [j-v[i]]，其中j和j-v[i]都是小于等于j的，在j的同一侧，所以我们综合以上两点原因就可以将二维优化到一维，即完成空间优化。

我们先来将二维和优化后的一维在关键算法代码上进行一下对比：

for(int i = 1; i <= n; i++) 
    for(int j = m; j >= 0; j--)
    {
        if(j < v[i]) 
            f[i][j] = f[i - 1][j];  // 优化前
            f[j] = f[j];            // 优化后，该行自动成立，可省略。
        else    
            f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);  // 优化前
            f[j] = max(f[j], f[j - v[i]] + w[i]);                   // 优化后
    }

实际上，只有当枚举的背包容量 >= v[i] 时才会更新状态，因此我们可以修改循环终止条件进一步优化。

for(int i=1;j<=n;i++)
{
	for(int j=m;j>=v[i];j--)
	{
		f[j]=max(f[j],f[j-v[i]]+w[i]);
	}
}

#include 
#include 

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

1.4思路三介绍(输入数据优化)

  我们注意到在处理数据时，我们是一个物品一个物品，一个一个体积的枚举。因此我们可以不必开两个数组记录体积和价值，而是边输入边处理。

#include

using namespace std;

const int MAXN = 1005;
int f[MAXN];  // 

int main() 
{
    int n, m;   
    cin >> n >> m;

    for(int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;      // 边输入边处理
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;

    return 0;
}

2.完全背包问题

2.1题目描述：

2.2思路一(朴素算法)

#include
using namespace std;
const int N=1010;
int f[N][N];
int n,m;
int v[N],w[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k*v[i]<=j;k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

上述朴素算法和01背包问题的朴素算法非常相似，但是会超时。所以我们接下来就会对这个算法进行优化处理。

2.3思路二(将k优化处理掉)

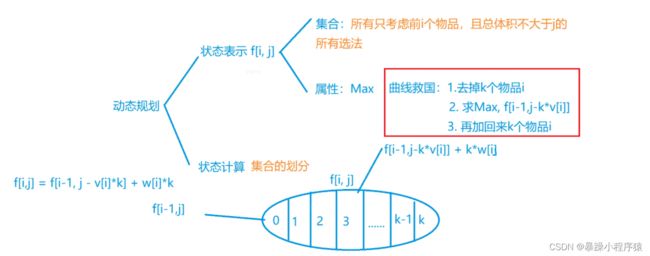
  我们先来分析一下状态转移方程，我们发现方程一和方程二有一定的联系，我们先不看方程一红色圈出来的部分，我们比较方程一黄色的部分和方程二的内容，我们发现方程一就是比方程二每一项多了一个w，那么我们黄色圈出来的部分的最大值也就比方程二的最大值多w，那么我们其实就可以将方程一圈出来黄色的部分进行等价替换，替换成红色方框黄色字体的内容，我们最终得出最下方的结论，其实我们要求得最大值之和两个状态有关，比较它们的最大值即可。

我们发现好像最后的状态转移方程和k并没有关系了，那么我们就干脆去掉k的那次循环

所以我们对核心代码进行了优化：

for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++)
{
    f[i][j] = f[i-1][j];//状态一，即不取第i个物品
    if(j-v[i]>=0)//判断是否可以加入第i个物品
        f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//状态二
}

完整代码如下：

#include
using namespace std;
const int N=1010;
int f[N][N];
int n,m;
int v[N],w[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])
            {
                f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

我们来比较一个完全背包的核心代码和01背包核心代码的区别:

//01背包问题核心优化后代码
for(int i=1;i<=n;i++)
{
	for(int j=m;j>=v[i];j--)
	{	f[i][j]=f[i-1][j];
		if(j>=v[i])
		{
			f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
		}
	}
}
//完全背包问题核心优化后代码
for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++)
{
    f[i][j] = f[i-1][j];//状态一，即不取第i个物品
    if(j-v[i]>=0)//判断是否可以加入第i个物品
        f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//状态二
}

我们发现其实本质也就是一句不同：注意i的下标

  我们这个i的下标是根据两个不同的背包问题的状态转移方程得出来的，我们01背包问题因为要使用第i-1层的数据，所以我们枚举j的时候只能从后往前枚举，这样做是因为j-v[i]小于j，那么f[j-v[i]]的数据就会被改，那么我们使用的数据其实就是第i层的数据了，不满足状态转移方程，所以我们要从后往前枚举，但是完全背包问题使用的就是第i层的数据，所以不存在从前往后枚举就会在使用前数据就发生意外改变的这种情况，所以就在这个地方这两个核心算法略有差别。

2.4思路三(优化j的初始条件)

这个和01背包问题的优化方法是一样的，就不多赘述了。

核心代码如下：

for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)//注意了，这里的j是从小到大枚举，和01背包不一样
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }

完整代码如下：

#include
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }

    for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
    cout<<f[m]<<endl;
}

总结

  本篇博客主要涉及动态规划背包问题的01背包问题和完全背包问题，给大家分享了实现的思路和代码模板，大家也可以看看yxc的背包九讲，图片转载于yxc，希望对大家有所帮助，后面会持续更新~