【AIOT】手势捕捉论文阅读笔记

---

title: Hand Analyse Record
date: 2020-06-20 11:32:44
author: liudongdong1
img: https://gitee.com/github-25970295/blogImage/raw/master/img/dataglove.jpg
reprintPolicy: cc_by
cover: false
categories: AIOT
tags:

• HandPose

---

level: CVPR CCF_A
author: Tomas Simon Carnegie Mellon University
date: 2017
keyword:

• hand pose

---

Paper: OpenPose HandKeypoint

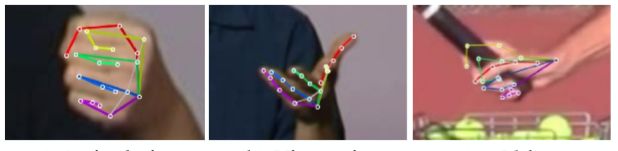
Hand Keypoint Detection in Single Images using Multiview Bootstrapping

Summary

1. present an approach that uses a multi-camera system to train fine-grained detectors for keypoints.

Research Objective

• Application Area: hand based HCI and robotics
• Purpose: to extract hand point coordinate from single RGB images.

Proble Statement

• self-occlusion due to articulation, view-point, grasped object.

previous work:

• many approaches to image-based face and body keypoint localization exist, there are no markerless hand keypoint detectors that work on RGB images in the wild.

Methods

• Problem Formulation:

input: a crop image patch $IϵR^{w\ast h\ast 3}$

output: P keypoint location, $X_pϵR^2$,with associated confidence $C_p$.
$$Keypointdetector:d(I)->[(X_p,c_p)forpϵ[\mathrm{1....}P]]$$

• system overview:

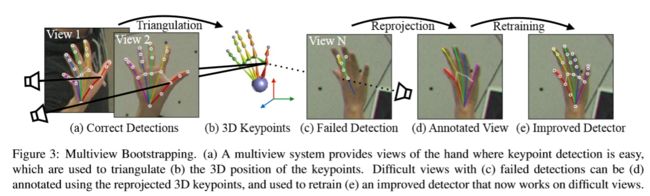
【Multiview Bootstrapped Training】

• $Initialtrainingset:T_0:=[(I_f,y_p^f)forfϵ[\mathrm{1...}{N}_0]]$, $f$ denote the particular image frame,set$[y_p^fϵR^2]$ include all labeled keypoints for image $I^f$ .

Multiview Bootrstrap:

• Inputs:
  • calibrated cameras configuration
  • unlabled images: $[I_v^{f}forvϵviews,fϵframes]$
  • keypoint detector: $d_0(I)->[(x_p,c_p)forpϵpoints]$
  • labeled training data: $T_0$
• Output: improved detector $d_K(.)$ and training set $T_k$
• for iteration $i$ in 0 to K:
  1. Triangulate keypoint from weak detections
     • for every frame $f$:
       • run detector $d_i(I_v^f)$ on all views $v$ , $D<-\{d_i(I_v^f)forvϵ[\mathrm{1...}V]\}$ (1)
       • robustly triangulate keypoints, $X_p^f=argmi{n}_X{\sum }_{vϵI_p^f}||P_v(X)-x_p^v|{|}_2^2$ (2)
  2. score and sort triangulated frames , $score(\{X_p^f\})={\sum }_{pϵ[\mathrm{1...}P]}{\sum }_{vϵI_p^f}{C}_p^v$ (3)
  3. retrain with N-best reprojections. $d_{i+1}<-train(T_{0}U{T}_{i+1})$ (4)

supplement for the mathmatic:

• for (1):for one frame, for each keypoint p, we have V detections $(x_p^v,c_p^v)$ , robustly triangulate each point p into a 3D location, use RANSAC on point D with confidence above a detection threshold $\lambda$.

• for (2): $I_p^f$ is the inlier set, $X_p^fϵR^3$ is the 3D triangulated keypoint p in frame f, $P_v(X)ϵR^2$ denotes projection of 3D point $X$ into view $v$. triangulate all landmarks of each finger(4 points ) at a time.

• for(3): pick the best frame for every window of $W$ frames. Sort the frame in descending order according to their score, to obtain an ordered sequence of frames,$[s_1,s_2,...s_F^{‘}]$, $F^{‘}$ is the number of subsampled frames, $s_i$ is the ordered frame index.

  • while verigy the good labled frame, using some strategies to automatically removing bad frame:
    • average number of inliews
    • average detection detection confidence
    • difference of per-point velocity with medium velocity between two video frames
    • anthropomorphic limits on joint lengths
    • complete occlusion as determined by camera ray intersection with body joints

• for(4): $T_{i+1}=\{(I_v^{s_n},\{P_v(X_p^{s_n}):vϵ[\mathrm{1...}V],pϵ[\mathrm{1...}P]\})fornϵ[\mathrm{1...}N]\}$

【Detection Architecture】

• Hand Bounding Box Detection: directly use the body pose estimation models from [29], and [4] and use wrist and elbow position to approximate the hand location, assuming the hand extends 0.15 times the length of the forearm(前臂) in the same direction.
• using architecture of CPMs with some modification. CPMs predict a confidence map for each keypoint, representing the keypoint’s location as a Gaussian centered at the true position
• using pre-trained VGG-19 network

Evaluation

• Environment:
  • Dataset:
    • the MPII human pose dataset[2] reflect every-day human activities
    • Images from the New Zealand Sign Language Exercised os the Victoria University of Wellington contains a variety of hand poses found in conversation

Conclusion

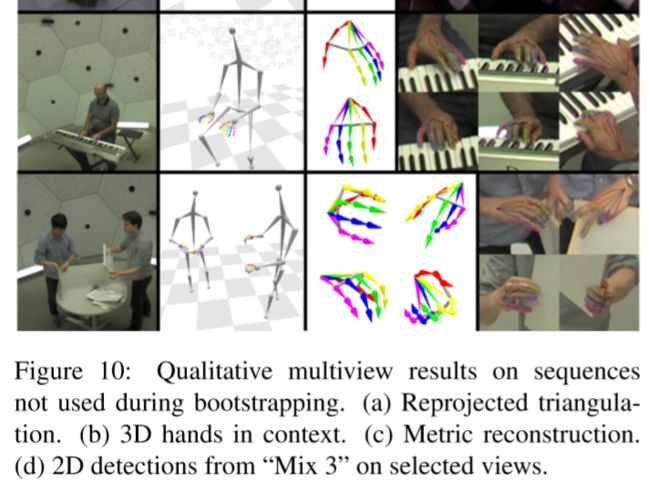
• the first real-time hand keypoint detector showing practical applicability to in-the-wild RGB videos
• the first markerless 3D hand motion capture system capable of reconstructing challenging hand-object interactions and musical performances without manual intervention
• using multi-view bootstrapping, improving both the quality and quantity of the annotations

Notes

• Bootstrap步骤：

  • 在原有的样本中通过重抽样抽取一定数量（比如100）的新样本。

  • 基于产生的新样本，计算我们需要估计的统计量${\alpha }_i$。

  • 重复上述步骤n次（一般是n>1000次）。计算被估计量的均值和方差。

  • $$\alpha =Mean({\alpha }_i...)$$

  • 

• RANSAC: robust estimation techniques such as M-estimators and least-median squares that have been adopted by the computer vision community from the statistics literature, RANSAC was developed from within the computer vision community

  

  

level: CVPR
author: Kuo Du1
date: 2019
keyword:

• hand skeleton

---

Paper: CrossInfoNet

CrossInfoNet: Multi-Task Information Sharing Based Hand Pose Estimation

Summary

1. proposed CrossInfoNet decomposes hand pose estimation task into palm pose estimation sub-task and finger pose estimation sub-task, and adopts two-branch cross-connection structure to share the beneficial complementary information between the sub-tasks.
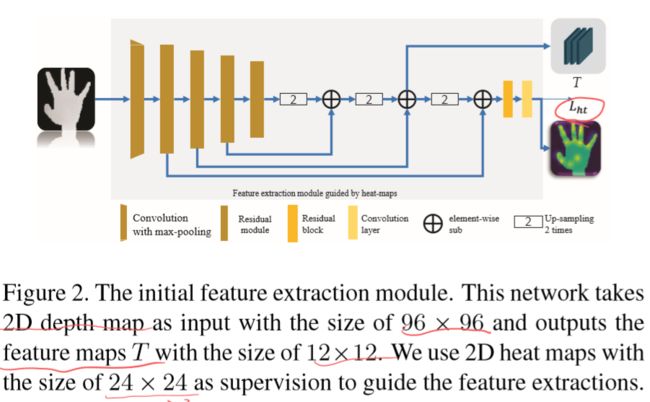
2. propose a heat-map guided feature extraction structure to get better feature maps, and train the complete network end-to-end.

Proble Statement

previous work:

• treating depth maps as 2D images and regressing 3D joint coordinates directly is a commonly used hand pose estimation pipeline.
• designing effective networks receives the most attentions. Learning multiple tasks simultaneously will be helpful to enforce a model with better generalizing ability.
• the output representations can be classified into the probability density map or the 3D coordinates for each joint. heat-map based method outperforms direct coordinate regression method, and the final joint coordinates have usually to be inferred by maximum operation on the heat-maps

Methods

• system overview:

【Heat-map guided feature extraction】

• ResNet-50 [15] backbone network with four residual modules
• apply the feature pyramid structure to merge different feature layers.
• the heat maps are only used as the constraints to guide the feature extraction and will not be passed to the subsequent module.

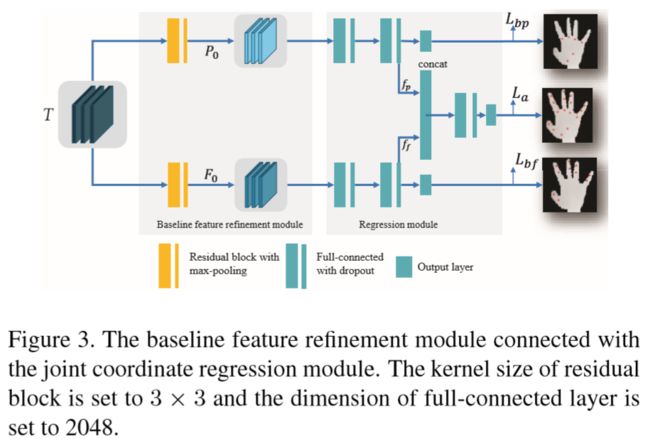
【Baseline feature refinement architecture】

【New Feature refinement architecture】

【Loss Functions Defines】

Evaluation

• Environment:
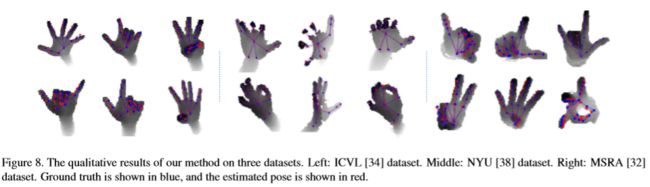
  • Dataset: ICVL datasets, NYU datasets, MSRA datasets, Hands 2017 Challenge Frame-based Dataset.

Conclusion

• use hierarchical model to decompose the final task into palm joint regression sub-task and finger joint regression sub-task.
• a heat-map guided feature extraction structure is proposed.

Notes 去加强了解

• https://github.com/dumyy/handpose

Paper: Emotion Identification

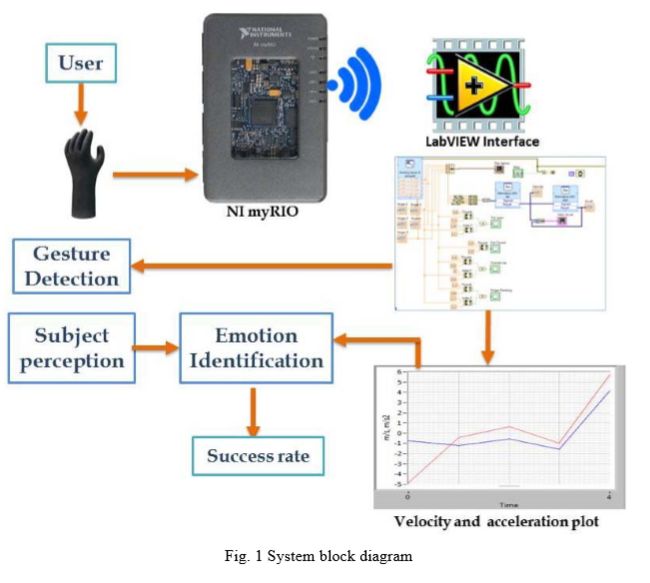
Hand Gestures Based Emotion Identification Using Flex Sensors

Summary

Paper: Gesture To Speech

Gesture To Speech Conversion using Flex sensors,MPY6050 and Python

Summary

• Arduino Uno, Flex Sensors, MPU6050 an accelerometer gyroscope sensor which is used to detect the alignment of an object.
• To recognise the ALS Sign Language
• 

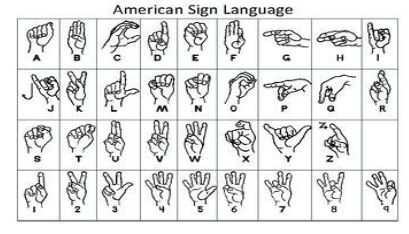
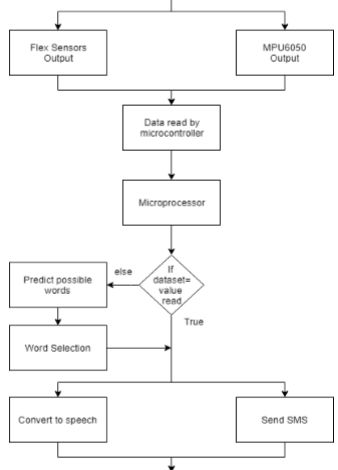
Paper: Flex

Flex: Hand Gesture Recognition using Muscle Flexing Sensors

Summary

• Flex Sensors from Spectra-Symbol for angle displacement measuremetns.

• apply a linear response delay filter to the raw sensors output for noise reduction and signal smoothing.

  

Paper: Survey on Hand Pose Estimation

A Survey on Hand Pose Estimation with Wearable Sensors and Computer-Vision- Based Methods

Summary

• 详细介绍了基于视觉基于传感器方法

  

Paper: Flex&Gyroscopes

Recognizing words in Thai Sign Language using flex sensors and gyroscopes

Summary

• some sensors

  • contact sensors for detecting fingers touching each other
  • accelerometers for measuring the acceleration of the hand in different direction
  • gyro-scopes for measuring the hand orientation and angular movement
  • magnetoresistive sensors for measuring the magnetic field for deriving the hand orientation

• presents a Thai sign language recognition framework using a glove-based device with flex sensors and gyro-scops.

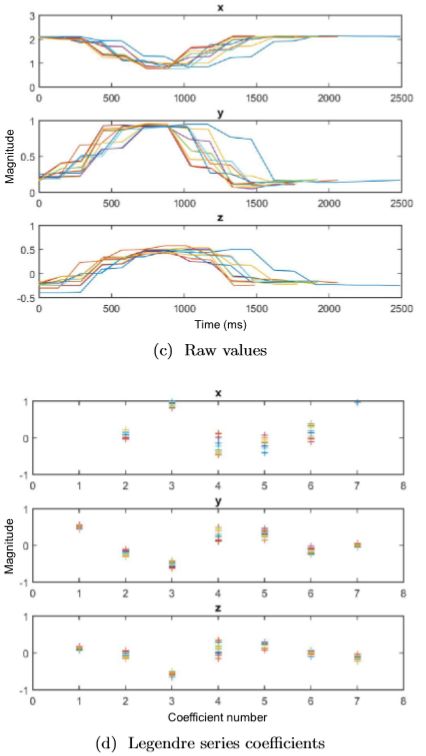
• the measurements from the sensors are processed using finite Legendre and Linear Discriminant Analysis, then classified using k-nearest neighbors.

• Handware design:

  

• the gyroscopes can return values in three different types of measurement

  • the quaternions are the raw data returned from the sensor. This measurement yields a four-dimensional output.
  • Euler angles are data converted from the four quaternion values. The Euler angles consist of three values, matching x, y, and z axis.
  • YPR measures the angle but with respect to the direction of the ground. It has three elements like the Euler angles. However it also requires gravity values from the accelerometer in order to calibrate. to calculate YPR, four quaternion elements and three gravity values are needed

• Date processing

  • segment and normalize the data ???how to segment data unclear??

  • the value from flex sensors differ greatly depend on person, by requiring a calibration phase which the user clenches and releases his hands at least 3 times to determine th e maximum and minimum values of each flex sensor, and quantize the data to 3 possible values(0,1,2)

  • 这部分不理解：

    

Human-Machine-Interaction

Taheri, Omid, et al. “GRAB: A dataset of whole-body human grasping of objects.” European Conference on Computer Vision. Springer, Cham, 2020.

---

Paper: GRAB

GRAB: A dataset of whole-body human grasping of objects

Summary

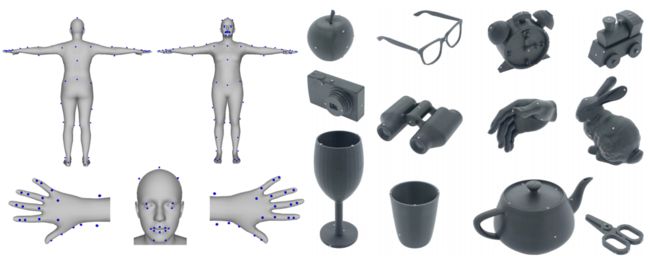
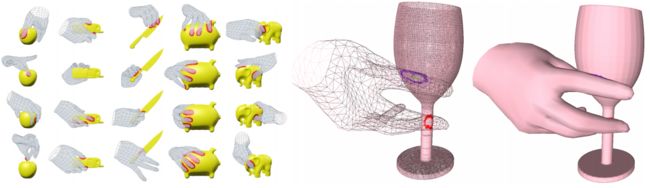
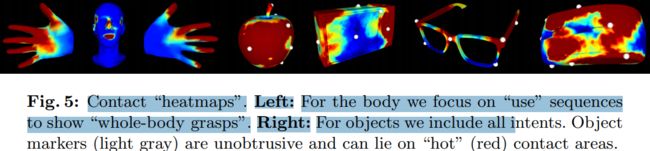
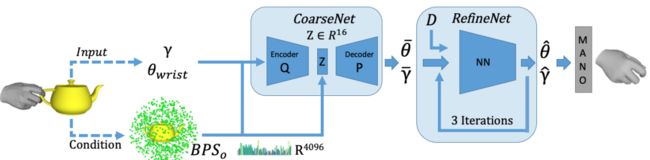
1. collect a new dataset, GRAB of whole-body grasps, containing full 3D shape and pose sequences of 10 subjects interacting with 51 every day objects of varying shape and size.
2. using MoCap markers to fit the full 3D body shape and pose, including the articulated face and hands, as well as the 3D object pose.
3. adapt MoSh++ to solve for the body, face, and hands of SMPL-X to obtain detailed moving 3D meshes, and according to the meshes and tracked 3D objects, we compute plausible contact on the object and the human and provide an analysis of observed patterns.

Relative

• require complex 3D object shapes, detailed contact information, hand pose and shape, and the 3D body motion over time;
• MoCap: https://mocap.reallusion.com/iClone-motion-live-mocap/

---

Paper: A Mobile Robot Hand-arm

A Mobile Robot Hand-Arm Teleoperation System by Vision and IMU

Summary

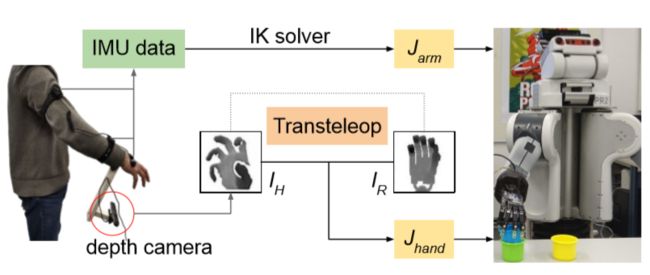
1. present a multi-modal mobile teleoperation system that consists of a novel vision-based hand pose regression network and IMU-based arm tracking methods.
2. observe the human hand through a depth camera and generates joint angles and depth images of paired robot hand poses through an image-to-image translation process.
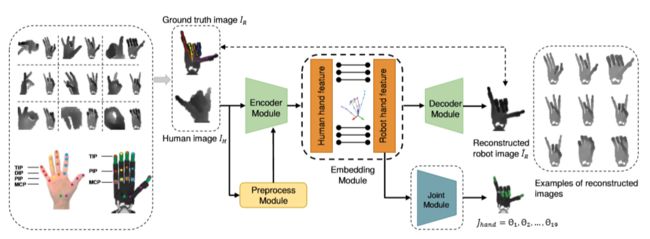
3. Transteleop takes the depth image of the human hand as input, then estimates the joint angles of the robot hand, and also generates the reconstructed image of the robot hand.
4. design a keypoint-based reconstruction loss to focus on the local reconstruction quality around the keypoints of the hand.

Research Objective

• Application Area: space, rescue, medical, surgery, imitation learning.
• Purpose: implement different manipulation tasks such as pick and place, cup insertion, object pushing, and dual-arm handover tasks

Proble Statement

• the robot hand and human hand occupy two different domains, how to compensate for kinematic differences between them plays an essential role in markerless vision-based teleoperation

previous work:

• Image-to-Image translation: aims to map representation of a scene into another, used in collection of style transfer, object transfiguration, and imitation learning.

Methodsj

• system overview:

【Question 1】how to discover the latent feature embedding the Zpose between the human hand and robot hand?

using Encoder-decoder module

【Question 2】how to get more accuracy of local features such as the position of fingertips instead of global features such as image style?

design a keypoint-based reconstruction loss to capture the overall structure of the hand and concentrate on the pixels around the 15 keypoints of the hand.

using mean squared error(MSE) loss to calculate the joint from $Z_R$ (robot feature)

【Question 3】the poses of the human hand vary considerably in their global orientations?

applied spatial transformation network(STN) provides spatial transformation capabilities of input images before the encoder module.

【Question 4】the hand easily disappears from the field of view of the camera, and the camera position is uncertain ?

using a cheap 3D-printed camera holder

using Perception Neuron device to control the arm of the robot.

Evaluation

• Environment:

  • Dataset: dataset of paired human-robot images, contains 400k pairs of simulated robot depth images and human hand depth images, the ground trush are 19 joint angles of the robot hand, record the 9 depth images of the robot hand from different viewpoints simultaneously corresponding to one human pose.

  

Notes 去加强了解

• https://Smilels.github.io/multimodal-translation-teleop
• 可能有什么问题，

level: PerDial’19
author:
date: 2019
keyword:

• robot, ASL,

---

Paper: Human-Robot

Human-Robot Interaction with Smart Shopping Trolley using Sign Language: Data Collection

Summary

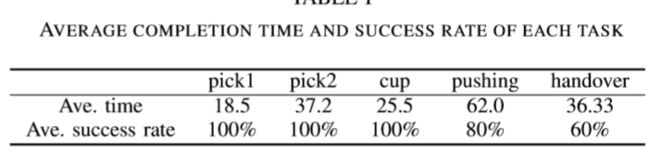
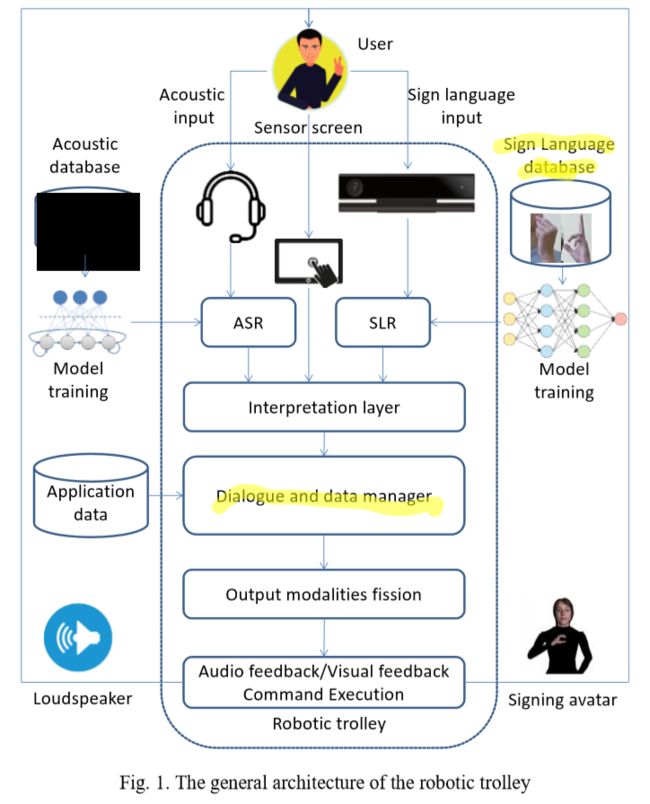
1. presents a concept of smart robotic trolley for supermarkets with multi-modal user interface, including sign language and acoustic speech recognition, and equipped with a touch screen.

Proble Statement

• continuous or dynamic sign language recognition remains an unresolved challenge.
• sensitivity to size and speed variations, poor performance under varying lighting conditions and complex background have limited the use of SLR in modern dialogue systems.

previous work:

• the level of voiced speech and isolated/static hand gesture automatic recognition quality is quite high.
• EffiBot[1] takes goods and automatically goes with them to the point of discharge, and follow the user when the corresponding mode is activated.
• The Dash Robotic Shopping Cart[2] :
  • a supermarket trolley that facilitates shopping and navigation in the store, the car is equipped with a touchscreen for entering a list of products of interest to the client.
• Gita by Piaggio[3]: a robotic trolley that follows the owner.
• none of the interfaces of the aforementioned robotic carts are multimodal.

Methods

• system overview:

  

1. speaker-independent system of automatic continuous Russian speech recognition
2. speaker-independent system of Russian sign language recognition with video processing using Kinect2.0 device
3. interactive graphical user interface with touchscreen
4. dialogue and data manager that access an application database, generates multi modal output and synchronizes input modalities fusion and output modalities fission
5. modules for audio-visual speech synthesis to be applied for a talking avatar

Conclusion

• understanding voice commands
• understanding Russian sign language commands
• escort the user to a certain place in the store
• speech synthesis, synthesis of answers in Russian sign language using a 3D avatar.

Notes

• 介绍了一些手语 数据集
• 【30】，32 ，7 ， 34
• 机器人：https://www.effidence.com/effibot
  • ​ https://mygita.com/#/how-does-gita-work

---

level: IJCAI
author: YangYi (MediaLab,Tencent) FengNi(PekingUniversity)
date: 2019
keyword:

• hand gesture understand

---

Paper: MKTB&GRB

High Performance Gesture Recognition via Effective and Efficient Temporal Modeling

Research Objective

• Purpose: hand gesture recognition instead of human-human or human-object relationships.

Proble Statement

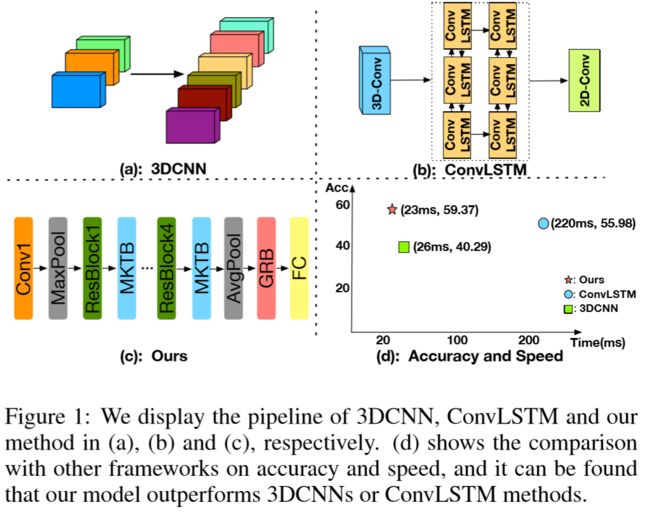
• hand gesture recognition methods based on spatio-temporal features using 3DCNNs or ConvLSTM suffer from the inefficiency due to high computational complexity of their structure.

previous work:

• Temporal Modeling for Action Recognition

  • 2DCNN by Narayana et al., 2018
  • 3DCNNs by Miao et al., 2017
  • ConvLSTM by Zhang et al., 2017
  • TSN by Wang et al.2016 models long-range temporal structures with segment-based sampling and aggregation module.
  • C3D by Li et al.2016 designs a 3DCNN with small 333 convolution kernels to learn spatiotemporal features.
  • I3D by Carreira 2017 inflates convolutional filters and pooling kernels into 3D structures.
  • R(2+1)D by Wang et al. 2018 present non-local operations to capture long-reange dependencies

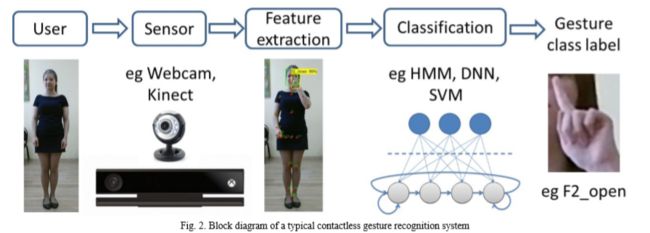
• Gesture Recognition:

  • 2DCNN by Narayana et al.2018 (学习下，多模态的,只了解多模态部分) fuses multi-channels(global/left-hand/right-hand/for RGB/depth/RGB-flow/Depth-flow modalities)
  • combines 3DCNN， bidirectional ConvLSTM and 2DCNN into a unified framework. ( 学习下如何整合到一个框架中)

  

Methods

• system overview:

  • the model builds upon TSN, for TSN lacks of capability of modeling the temporal information from feature-space, the proposed MKTB and GRB are effective temporal modeling modules in feature-space.

【Multi-Kernel Temporal Block】

• unlike 3DCNNs, performing convolutional operation for both spatial and temporal dimension jointly, the MTKB decouples the joint spatial-temporal modeling process and focuses on learning the temporal information.
• the design of multi-kernel works well on shaping the pyramidal and discriminative temporal features.

• define feature maps from layer $l$ of 2DCNN(ResNet-50) as $F_sϵR^{(B\ast T)\ast C\ast H\ast W}$
• reduce the channels of $F_s$ via convolution layer with kernel size of 1*1, denoted as $F_s^{‘}ϵR^{(B\ast T)\ast C^{‘}\ast H\ast W}$
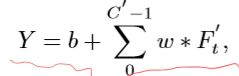• using depthwise temporal conv [Chollet,2017]

【Global Refinement Block】

• MKTB mainly focuses on the local neighborhoods,but the global temporal features across channels are not sufficiently attended.

• GRB is designed to perform the weighted temporal aggregation, in which it allows distant temporal features to contribute to the filtered temporal features according to the cross-similarity. 遗留问题，如何计算similarity， MKTB 中如何sum

  

Evaluation

• 

Conclusion

• MKTB captures both short-term and long-term temporal information by using the multiple 1D depthwise convolutions.
• MKTB and GRB maintain the same size between input and output, and can be easily deployed everywhere.

Notes 去加强了解

• https://github.com/nemonameless/Gesture-Recognition

level: CCF_A CVPR
author: Liuhao Ge, Nanyang Technological University
date: 2018
keyword:

• hand pose

---

Paper: Hand PointNet

Hand PointNet: 3D Hand Pose Estimation using Point Sets

Summary

1. propose HandPointNet model, that directly processes the 3D point cloud that models the visible surface of the hand for pose regression,Taking the normalized point cloud as the input, the regression network capture complex hand structures and accurately regress a low dimensional representation of the 3D hand pose.
2. design a fingertip refinement network that directly takes the neighboring points of the estimated fingertip location as input to refine the fingertip location.

Research Objective

• Application Area: hand based interaction
• Purpose: exact hand skeleton

Proble Statement

• high dimensionality of 3D hand pose, large variations in hand orientations, high self-similarity of fingers and servere self-occlusion

previous work:

• large hand pose datasets[38, 34, 33, 49, 48]
• CNN model:
  • the time and space complexities of the 3D CNN grow cubically with the resolution of the input 3D volume, using low resolution may lose useful details of the hand
  • PointNet: perform 3D object classification and segmentation on point sets directly
  • using multi-view CNNs-based method and 3D CNN-based method
• Hand Pose Estimation: Discriminative approaches, generative approaches, hybrid approaches
  • feedback loop model[21]
  • spatial attention network[47]
  • deep generative models[41]
• 3D Deep Learning:
  • Multi-view CNNs-based approaches[32, 24, 7, 2] project 3D points into 2D images and use 2D CNNs to process them.
  • 3D CNNs based on octrees[27, 43] are proposed for efficient computation on high resolution volumes.

Methods

• Problem Formulation:

• Input: depth image containing a hand;

• outputs: a set of 3D hand joint locations in the amera coordinate system.

• system overview:

【Basic PointNet】 [23] directly takes a set of points as the input and is able to extract discriminative features of the point cloud. cannot capture local structures of the point cloud in a hierarchical way.

basic architecture of PointNet takes N points as the input, Each D-dim input point is mapped into a C-dim feature through MLP. Per-point features are aggregated into a global feature by max-pooling, and mapped into F-dim output vector.

【Hierarchical PointNet】[25]:

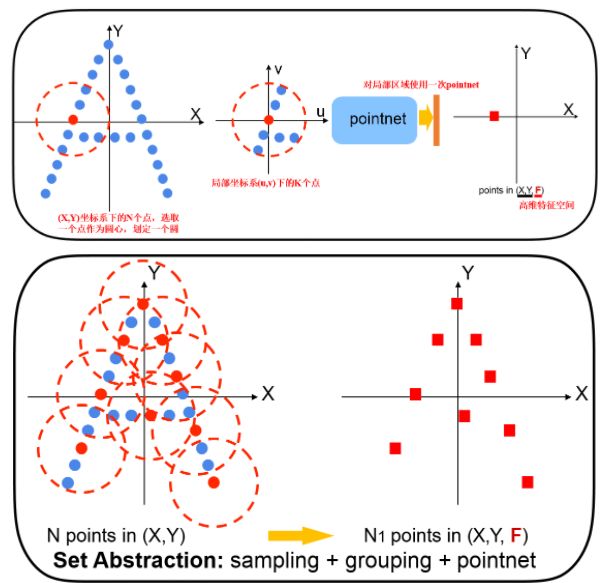
The hierarchical structure is composed by a number of set abstraction levels, at each level, a set of points is processed and abstracted to produce a new set with fewer elements. The set abstraction level is made of three key layers: 点云采样+成组+提取局部特征（S+G+P）的方式，包含这三部分的机构称为 Set Abstraction

• sampling layer: selects a set of points from input points, which defines the centroids of lcoal regions. use interative farthest point sampling(FPS) to choose the subset of points.
• grouping layer: constructs local region sets by fining “neighboring” points around the centroids. N`K(d+C): d-dim coordinates, and C-dim point feature, K is the number of points in the neighborhood of centroid points. Ball query finds all points that are within a radius to the query point.
• PointNet alyer: uses a mini-PointNet to encode local region patterns into feaature vectors.

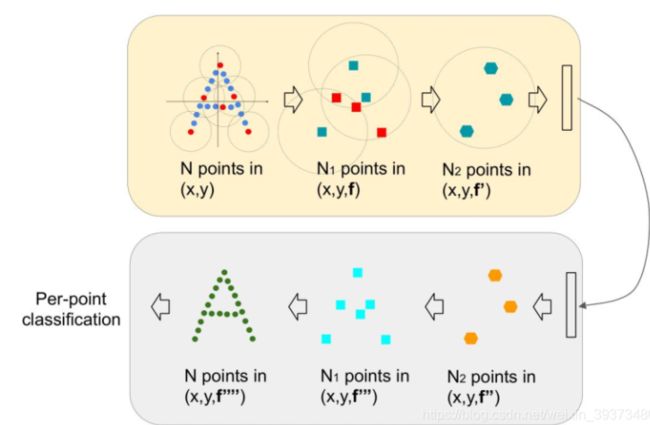
• 分类网络是逐层提取特征，最后总结出全局特征。
• 分割网络先将点云提取一个全局特征，在通过这个全局特征逐步上采样。每层新的中心点都是从上一层抽取的特征子集，中心点的个数就是成组的点集数，随着层数增加，中心点的个数也会逐渐降低，抽取到点云的局部结构特征。当点云不均匀时，每个子区域中如果在分区的时候使用相同的球半径，会导致部分稀疏区域采样点过小。多尺度成组 (MSG)和多分辨率成组 (MRG)
  • **多尺度成组（MSG）：**对于选取的一个中心点设置多个半径进行成组，并将经过PointNet对每个区域抽取后的特征进行拼接（concat）来当做该中心点的特征.
  • **多分辨率成组（MRG）：**对不同特征层上（分辨率）提取的特征再进行concat，以上图右图为例，最后的concat包含左右两个部分特征，分别来自底层和高层的特征抽取，对于low level点云成组后经过一个pointnet和high level的进行concat，思想是特征的抽取中的跳层连接。当局部点云区域较稀疏时，上层提取到的特征可靠性可能比底层更差，因此考虑对底层特征提升权重。当然，点云密度较高时能够提取到的特征也会更多。这种方法优化了直接在稀疏点云上进行特征抽取产生的问题，且相对于MSG的效率也较高。

【OBB-based Point Cloud Normalization】to deal with large variation in global orientation of the hand. normalization the hand point cloud into a canonical coordinate system in which the global orientations of the transformed hand point clouds are as consistent as possible. normalization step ensures that our method is robust to variations in hand global orientations

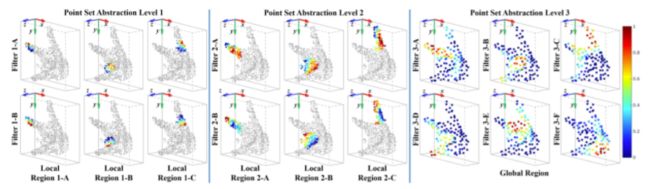
each column corresponds to the same local region, and each row correspnd to the same filter. Following pictures show the sensitivity of points in three loacl regions to two fitlers at each of the first two levels.

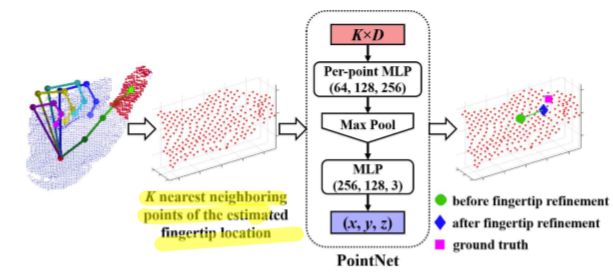
【Refine the Fingertip】

Based on the obervation: the fingertip location of straightened finger is usually easy to be fined, since K nearest neighboring points of the fingertip will not change a lot even if the estimated location deviates from the ground truth location to some extent when K is relatively large

Conclusion

• estimate 3D hand joint locations directly from 3D point cloud base on the netword architecture of PointNet. better expoit the 3D spatial information in the depth image
• robust to variations in hand global orientations, normalize the sampled 3D points in an oriented bounding box without applying any additional network to transform the hand piont cloud.
• refine the fingertip locations with a basic PointNet that takes the Neighboring points of the estimation fingertip location as input to regress the refined fingertip location.

Notes 去加强了解

1. 最远点采样

最远点采样(Farthest Point Sampling)是一种非常常用的采样算法，由于能够保证对样本的均匀采样，被广泛使用，像3D点云深度学习框架中的PointNet++对样本点进行FPS采样再聚类作为感受野，3D目标检测网络VoteNet对投票得到的散乱点进行FPS采样再进行聚类，6D位姿估计算法PVN3D中用于选择物体的8个特征点进行投票并计算位姿。

1. 输入点云有N个点，从点云中选取一个点P0作为起始点，得到采样点集合S={P0}；
2. 计算所有点到P0的距离，构成N维数组L，从中选择最大值对应的点作为P1，更新采样点集合S={P0，P1}；
3. 计算所有点到P1的距离，对于每一个点Pi，其距离P1的距离如果小于L[i]，则更新L[i] = d(Pi, P1)，因此，数组L中存储的一直是每一个点到采样点集合S的最近距离；
4. 选取L中最大值对应的点作为P2，更新采样点集合S={P0，P1，P2}；
5. 重复2-4步，一直采样到N’个目标采样点为止。

• 初始点选择：
  • 随机选择一个点，每次结果不同；
  • 选择距离点云重心的最远点，每次结果相同，一般位于局部极值点，具有刻画能力；
• 距离度量
  • 欧氏距离：主要对于点云，在3D体空间均匀采样；
  • 测地距离：主要对于三角网格，在三角网格面上进行均匀采样；

from __future__ import print_function
import torch
from torch.autograd import Variable

def farthest_point_sample(xyz, npoint): 

    """
    Input:
        xyz: pointcloud data, [B, N, 3]
        npoint: number of samples
    Return:
        centroids: sampled pointcloud index, [B, npoint]
    """

    xyz = xyz.transpose(2,1)
    device = xyz.device
    B, N, C = xyz.shape
    
    centroids = torch.zeros(B, npoint, dtype=torch.long).to(device)     # 采样点矩阵（B, npoint）
    distance = torch.ones(B, N).to(device) * 1e10                       # 采样点到所有点距离（B, N）

    batch_indices = torch.arange(B, dtype=torch.long).to(device)        # batch_size 数组

    #farthest = torch.randint(0, N, (B,), dtype=torch.long).to(device)  # 初始时随机选择一点
    
    barycenter = torch.sum((xyz), 1)                                    #计算重心坐标 及 距离重心最远的点
    barycenter = barycenter/xyz.shape[1]
    barycenter = barycenter.view(B, 1, 3)

    dist = torch.sum((xyz - barycenter) ** 2, -1)
    farthest = torch.max(dist,1)[1]                                     #将距离重心最远的点作为第一个点

    for i in range(npoint):
        print("-------------------------------------------------------")
        print("The %d farthest pts %s " % (i, farthest))
        centroids[:, i] = farthest                                      # 更新第i个最远点
        centroid = xyz[batch_indices, farthest, :].view(B, 1, 3)        # 取出这个最远点的xyz坐标
        dist = torch.sum((xyz - centroid) ** 2, -1)                     # 计算点集中的所有点到这个最远点的欧式距离
        print("dist    : ", dist)
        mask = dist < distance
        print("mask %i : %s" % (i,mask))
        distance[mask] = dist[mask]                                     # 更新distance，记录样本中每个点距离所有已出现的采样点的最小距离
        print("distance: ", distance)

        farthest = torch.max(distance, -1)[1]                           # 返回最远点索引
 
    return centroids

if __name__ == '__main__':

    sim_data = Variable(torch.rand(1,3,8))
    print(sim_data)

    centroids = farthest_point_sample(sim_data, 4)
    
    print("Sampled pts: ", centroids)

2. PointNet网络结构

数据集中每一行是六个点，及每一点有六个特征（3d坐标，法向量）normal意思是法向量，可以自己设置，要不要使用法向量，使用的话初始输入的点云数据除了3个位置信息x，y，z以外还有三个法向量Nx，Ny，Nz，每个点一共是6个特征。

class PointNetEncoder(nn.Module):
    def __init__(self, global_feat=True, feature_transform=False, channel=3):
        super(PointNetEncoder, self).__init__()
        self.stn = STN3d(channel)
        self.conv1 = torch.nn.Conv1d(channel, 64, 1)
        self.conv2 = torch.nn.Conv1d(64, 128, 1)
        self.conv3 = torch.nn.Conv1d(128, 1024, 1)
        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(1024)
        self.global_feat = global_feat
        self.feature_transform = feature_transform
        if self.feature_transform:
            self.fstn = STNkd(k=64)

    def forward(self, x):
        B, D, N = x.size()
        trans = self.stn(x)
        x = x.transpose(2, 1)
        if D > 3:
            feature = x[:, :, 3:]
            x = x[:, :, :3]
        x = torch.bmm(x, trans)
        if D > 3:
            x = torch.cat([x, feature], dim=2)
        x = x.transpose(2, 1)
        x = F.relu(self.bn1(self.conv1(x)))

        if self.feature_transform:
            trans_feat = self.fstn(x)
            x = x.transpose(2, 1)
            x = torch.bmm(x, trans_feat)
            x = x.transpose(2, 1)
        else:
            trans_feat = None

        pointfeat = x
        x = F.relu(self.bn2(self.conv2(x)))
        x = self.bn3(self.conv3(x))
        x = torch.max(x, 2, keepdim=True)[0]
        x = x.view(-1, 1024)
        if self.global_feat:
            return x, trans, trans_feat
        else:
            x = x.view(-1, 1024, 1).repeat(1, 1, N)
            return torch.cat([x, pointfeat], 1), trans, trans_feat

class PointNetCls(nn.Module):
    def __init__(self, k = 2):
        super(PointNetCls, self).__init__()
        self.k = k
        self.feat = PointNetEncoder(global_feat=False)
        self.conv1 = torch.nn.Conv1d(1088, 512, 1)
        self.conv2 = torch.nn.Conv1d(512, 256, 1)
        self.conv3 = torch.nn.Conv1d(256, 128, 1)
        self.conv4 = torch.nn.Conv1d(128, self.k, 1)
        self.bn1 = nn.BatchNorm1d(512)
        self.bn2 = nn.BatchNorm1d(256)
        self.bn3 = nn.BatchNorm1d(128)

    def forward(self, x):
    	'''分类网络'''
        batchsize = x.size()[0]
        n_pts = x.size()[2]
        x, trans = self.feat(x)
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x)))
        x = self.conv4(x)
        x = x.transpose(2,1).contiguous()
        x = F.log_softmax(x.view(-1,self.k), dim=-1)
        x = x.view(batchsize, n_pts, self.k)
        return x


class PointNetPartSeg(nn.Module):
    def __init__(self,num_class):
        super(PointNetPartSeg, self).__init__()
        self.k = num_class
        self.feat = PointNetEncoder(global_feat=False)
        self.conv1 = torch.nn.Conv1d(1088, 512, 1)
        self.conv2 = torch.nn.Conv1d(512, 256, 1)
        self.conv3 = torch.nn.Conv1d(256, 128, 1)
        self.conv4 = torch.nn.Conv1d(128, self.k, 1)
        self.bn1 = nn.BatchNorm1d(512)
        self.bn1_1 = nn.BatchNorm1d(1024)
        self.bn2 = nn.BatchNorm1d(256)
        self.bn3 = nn.BatchNorm1d(128)

    def forward(self, x):
        '''分割网络'''
        batchsize = x.size()[0]
        n_pts = x.size()[2]
        x, trans = self.feat(x)
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x)))
        x = self.conv4(x)
        x = x.transpose(2,1).contiguous()
        x = F.log_softmax(x.view(-1,self.k), dim=-1)
        x = x.view(batchsize, n_pts, self.k)
        return x, trans

通过引入了不同分辨率/尺度的Grouping去对局部做PointNet求局部的全局特征，最后再将不同尺度的特征拼接起来；同时也通过在训练的时候随机删除一部分的点来增加模型的缺失鲁棒性。 -->解决点稀疏问题

3. PointNet++ 网络结构

import torch.nn as nn
import torch.nn.functional as F
from pointnet2_utils import PointNetSetAbstraction
import torch
import numpy as np

class get_model(nn.Module):
    def __init__(self,num_class,normal_channel=True):
        super(get_model, self).__init__()
        in_channel = 6 if normal_channel else 3
        self.normal_channel = normal_channel
        self.sa1 = PointNetSetAbstraction(npoint=512, radius=0.2, nsample=32, in_channel=in_channel, mlp=[64, 64, 128], group_all=False)
        self.sa2 = PointNetSetAbstraction(npoint=128, radius=0.4, nsample=64, in_channel=128 + 3, mlp=[128, 128, 256], group_all=False)
        self.sa3 = PointNetSetAbstraction(npoint=None, radius=None, nsample=None, in_channel=256 + 3, mlp=[256, 512, 1024], group_all=True)
        self.fc1 = nn.Linear(1024, 512)
        self.bn1 = nn.BatchNorm1d(512)
        self.drop1 = nn.Dropout(0.4)
        self.fc2 = nn.Linear(512, 256)
        self.bn2 = nn.BatchNorm1d(256)
        self.drop2 = nn.Dropout(0.4)
        self.fc3 = nn.Linear(256, num_class)

    def forward(self, xyz):
        B, _, _ = xyz.shape
        print("xyz.shape",xyz.shape)
        if self.normal_channel:
            norm = xyz[:, 3:, :]
            xyz = xyz[:, :3, :]
        else:
            norm = None
        l1_xyz, l1_points = self.sa1(xyz, norm)
        l2_xyz, l2_points = self.sa2(l1_xyz, l1_points)
        l3_xyz, l3_points = self.sa3(l2_xyz, l2_points)
        x = l3_points.view(B, 1024)
        x = self.drop1(F.relu(self.bn1(self.fc1(x))))
        x = self.drop2(F.relu(self.bn2(self.fc2(x))))
        x = self.fc3(x)
        x = F.log_softmax(x, -1)


        return x, l3_points



class get_loss(nn.Module):
    def __init__(self):
        super(get_loss, self).__init__()

    def forward(self, pred, target, trans_feat):
        total_loss = F.nll_loss(pred, target)

        return total_loss


if __name__ == "__main__":
    data = torch.ones([24,3,1024])
    print(data.shape)
    model = get_model(num_class=40,normal_channel=False)
    print(model)
    parameters = filter(lambda p: p.requires_grad, model.parameters())
    parameters = sum([np.prod(p.size()) for p in parameters]) / 1_000_000
    print('Trainable Parameters: %.3fM' % parameters)
    pred, trans_feat  = model(data)

    print("Shape of out :", pred.shape)  # [10,30,10]

get_model(
  (sa1): PointNetSetAbstraction(
    (mlp_convs): ModuleList(
      (0): Conv2d(3, 64, kernel_size=(1, 1), stride=(1, 1))
      (1): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1))
      (2): Conv2d(64, 128, kernel_size=(1, 1), stride=(1, 1))
    )
    (mlp_bns): ModuleList(
      (0): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (sa2): PointNetSetAbstraction(
    (mlp_convs): ModuleList(
      (0): Conv2d(131, 128, kernel_size=(1, 1), stride=(1, 1))
      (1): Conv2d(128, 128, kernel_size=(1, 1), stride=(1, 1))
      (2): Conv2d(128, 256, kernel_size=(1, 1), stride=(1, 1))
    )
    (mlp_bns): ModuleList(
      (0): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (sa3): PointNetSetAbstraction(
    (mlp_convs): ModuleList(
      (0): Conv2d(259, 256, kernel_size=(1, 1), stride=(1, 1))
      (1): Conv2d(256, 512, kernel_size=(1, 1), stride=(1, 1))
      (2): Conv2d(512, 1024, kernel_size=(1, 1), stride=(1, 1))
    )
    (mlp_bns): ModuleList(
      (0): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (2): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (fc1): Linear(in_features=1024, out_features=512, bias=True)
  (bn1): BatchNorm1d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (drop1): Dropout(p=0.4, inplace=False)
  (fc2): Linear(in_features=512, out_features=256, bias=True)
  (bn2): BatchNorm1d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (drop2): Dropout(p=0.4, inplace=False)
  (fc3): Linear(in_features=256, out_features=40, bias=True)
)

4. HandPointNet 代码阅读

• 数据处理部分

% create point cloud from depth image
% author: Liuhao Ge

clc;clear;close all;
%使用 fread，文件标识符无效。使用 fopen 生成有效的文件标识符。 这个错误是文件路径不对。
dataset_dir='C:\Users\liudongdong\OneDrive - tju.edu.cn\桌面\HandPointNet\data\cvpr15_MSRAHandGestureDB\';%'../data/cvpr15_MSRAHandGestureDB/'
save_dir='./';
subject_names={'P0','P1','P2','P3','P4','P5','P6','P7','P8'};
%subject_names={'P0'};
%gesture_names={'1'};
gesture_names={'1','2','3','4','5','6','7','8','9','I','IP','L','MP','RP','T','TIP','Y'};

JOINT_NUM = 21;
SAMPLE_NUM = 1024;
sample_num_level1 = 512;
sample_num_level2 = 128;

load('msra_valid.mat');

for sub_idx = 1:length(subject_names)
    mkdir([save_dir subject_names{sub_idx}]);
    
    for ges_idx = 1:length(gesture_names)
        gesture_dir = [dataset_dir subject_names{sub_idx} '/' gesture_names{ges_idx}];
        depth_files = dir([gesture_dir, '/*.bin']);
        
        % 1. read ground truth
        fileID = fopen([gesture_dir '/joint.txt']);
        
        frame_num = fscanf(fileID,'%d',1);    % 读取帧的个数
        A = fscanf(fileID,'%f', frame_num*21*3);   % 读取所有帧的关键点数据
        gt_wld=reshape(A,[3,21,frame_num]);     % 数据reshape操作
        gt_wld(3,:,:) = -gt_wld(3,:,:);
        gt_wld=permute(gt_wld, [3 2 1]);
        
        fclose(fileID);
        
        % 2. get point cloud and surface normal
        save_gesture_dir = [save_dir subject_names{sub_idx} '/' gesture_names{ges_idx}];  %matlab 文件拼接
        mkdir(save_gesture_dir);    %创建存储的路径文件
        
        display(save_gesture_dir);    %显示变量的信息
        
        Point_Cloud_FPS = zeros(frame_num,SAMPLE_NUM,6);
        Volume_rotate = zeros(frame_num,3,3);
        Volume_length = zeros(frame_num,1);
        Volume_offset = zeros(frame_num,3);
        Volume_GT_XYZ = zeros(frame_num,JOINT_NUM,3);
        valid = msra_valid{sub_idx, ges_idx};
        
        for frm_idx = 1:length(depth_files)
            if ~valid(frm_idx)                 %valid 数组主要用于判断这个数据帧是不是有效的
                continue;
            end
            %% 2.1 read binary file
            fileID = fopen([gesture_dir '/' num2str(frm_idx-1,'%06d'), '_depth.bin']);   %num2str(id,'%06d')  文件数据格式
            img_width = fread(fileID,1,'int32');
            img_height = fread(fileID,1,'int32');

            bb_left = fread(fileID,1,'int32');
            bb_top = fread(fileID,1,'int32');
            bb_right = fread(fileID,1,'int32');
            bb_bottom = fread(fileID,1,'int32');
            bb_width = bb_right - bb_left;
            bb_height = bb_bottom - bb_top;

            valid_pixel_num = bb_width*bb_height;

            hand_depth = fread(fileID,[bb_width, bb_height],'float32');     %读取手部区域有效的深度信息
            hand_depth = hand_depth';
            
            fclose(fileID);
            
            %% 2.2 convert depth to xyz
            fFocal_MSRA_ = 241.42;	% mm
            hand_3d = zeros(valid_pixel_num,3);
            for ii=1:bb_height
                for jj=1:bb_width
                    idx = (jj-1)*bb_height+ii;      % 手部区域深度图中每一个像素索引，按列优先
                    hand_3d(idx, 1) = -(img_width/2 - (jj+bb_left-1))*hand_depth(ii,jj)/fFocal_MSRA_;
                    hand_3d(idx, 2) = (img_height/2 - (ii+bb_top-1))*hand_depth(ii,jj)/fFocal_MSRA_;
                    hand_3d(idx, 3) = hand_depth(ii,jj);     % 深度距离值，   这个真实的z应该  是x*x+y*y+z*z=d*d  ??
                end
            end

            valid_idx = 1:valid_pixel_num;
            valid_idx = valid_idx(hand_3d(:,1)~=0 | hand_3d(:,2)~=0 | hand_3d(:,3)~=0);
            hand_points = hand_3d(valid_idx,:);             %过滤无效的数据

            jnt_xyz = squeeze(gt_wld(frm_idx,:,:));
            
            %% 2.3 create OBB
            [coeff,score,latent] = pca(hand_points);   %coeff = pca(X) 返回 n×p 数据矩阵 X 的主成分系数，也称为载荷。X 的行对应于观测值，列对应于变量。
                                              %系数矩阵是 p×p 矩阵。coeff 的每列包含一个主成分的系数，并且这些列按成分方差的降序排列。默认情况下，pca 将数据中心化，并使用奇异值分解 (SVD) 算法。
            if coeff(2,1)<0
                coeff(:,1) = -coeff(:,1);
            end
            if coeff(3,3)<0
                coeff(:,3) = -coeff(:,3);
            end
            coeff(:,2)=cross(coeff(:,3),coeff(:,1));   % 这里几步不太明白作用？

            ptCloud = pointCloud(hand_points);

            hand_points_rotate = hand_points*coeff;    %类似归一化处理，是的bounding box 的朝向基本一致

            %% 2.4 sampling                        %数据少的时候只是在原有的点基础上重复使用了一些点，  这里不知道可不可以直接使用
            if size(hand_points,1)<SAMPLE_NUM
                tmp = floor(SAMPLE_NUM/size(hand_points,1));
                rand_ind = [];
                for tmp_i = 1:tmp
                    rand_ind = [rand_ind 1:size(hand_points,1)];
                end
                rand_ind = [rand_ind randperm(size(hand_points,1), mod(SAMPLE_NUM, size(hand_points,1)))];  %返回行向量，其中包含在 1 到 size(hand_points,1) 之间随机选择的 k 个唯一整数。  
            else
                rand_ind = randperm(size(hand_points,1),SAMPLE_NUM);
            end
            hand_points_sampled = hand_points(rand_ind,:);
            hand_points_rotate_sampled = hand_points_rotate(rand_ind,:);
            
            %% 2.5 compute surface normal
            normal_k = 30;
            normals = pcnormals(ptCloud, normal_k);
            normals_sampled = normals(rand_ind,:);

            sensorCenter = [0 0 0];
            for k = 1 : SAMPLE_NUM
               p1 = sensorCenter - hand_points_sampled(k,:);
               % Flip the normal vector if it is not pointing towards the sensor.
               angle = atan2(norm(cross(p1,normals_sampled(k,:))),p1*normals_sampled(k,:)');
               if angle > pi/2 || angle < -pi/2
                   normals_sampled(k,:) = -normals_sampled(k,:);
               end
            end
            normals_sampled_rotate = normals_sampled*coeff;

            %% 2.6 Normalize Point Cloud    %通过每一轴的最值*scale进行 缩放处理
            x_min_max = [min(hand_points_rotate(:,1)), max(hand_points_rotate(:,1))];
            y_min_max = [min(hand_points_rotate(:,2)), max(hand_points_rotate(:,2))];
            z_min_max = [min(hand_points_rotate(:,3)), max(hand_points_rotate(:,3))];

            scale = 1.2;
            bb3d_x_len = scale*(x_min_max(2)-x_min_max(1));
            bb3d_y_len = scale*(y_min_max(2)-y_min_max(1));
            bb3d_z_len = scale*(z_min_max(2)-z_min_max(1));
            max_bb3d_len = bb3d_x_len;

            hand_points_normalized_sampled = hand_points_rotate_sampled/max_bb3d_len;
            if size(hand_points,1)<SAMPLE_NUM
                offset = mean(hand_points_rotate)/max_bb3d_len;
            else
                offset = mean(hand_points_normalized_sampled);
            end
            hand_points_normalized_sampled = hand_points_normalized_sampled - repmat(offset,SAMPLE_NUM,1);

            %% 2.7 FPS Sampling
            pc = [hand_points_normalized_sampled normals_sampled_rotate];
            % 1st level
            sampled_idx_l1 = farthest_point_sampling_fast(hand_points_normalized_sampled, sample_num_level1)';
            other_idx = setdiff(1:SAMPLE_NUM, sampled_idx_l1);
            new_idx = [sampled_idx_l1 other_idx];
            pc = pc(new_idx,:);
            % 2nd level
            sampled_idx_l2 = farthest_point_sampling_fast(pc(1:sample_num_level1,1:3), sample_num_level2)';
            other_idx = setdiff(1:sample_num_level1, sampled_idx_l2);
            new_idx = [sampled_idx_l2 other_idx];
            pc(1:sample_num_level1,:) = pc(new_idx,:);
            
            %% 2.8 ground truth
            jnt_xyz_normalized = (jnt_xyz*coeff)/max_bb3d_len;
            jnt_xyz_normalized = jnt_xyz_normalized - repmat(offset,JOINT_NUM,1);

            Point_Cloud_FPS(frm_idx,:,:) = pc;
            Volume_rotate(frm_idx,:,:) = coeff;
            Volume_length(frm_idx) = max_bb3d_len;
            Volume_offset(frm_idx,:) = offset;
            Volume_GT_XYZ(frm_idx,:,:) = jnt_xyz_normalized;
        end
        % 3. save files
        save([save_gesture_dir '/Point_Cloud_FPS.mat'],'Point_Cloud_FPS');
        save([save_gesture_dir '/Volume_rotate.mat'],'Volume_rotate');
        save([save_gesture_dir '/Volume_length.mat'],'Volume_length');
        save([save_gesture_dir '/Volume_offset.mat'],'Volume_offset');
        save([save_gesture_dir '/Volume_GT_XYZ.mat'],'Volume_GT_XYZ');
        save([save_gesture_dir '/valid.mat'],'valid');
    end
end

• 网络代码部分

nstates_plus_1 = [64,64,128]
nstates_plus_2 = [128,128,256]
nstates_plus_3 = [256,512,1024,1024,512]

class PointNet_Plus(nn.Module):
    def __init__(self, opt):
        super(PointNet_Plus, self).__init__()
        self.num_outputs = opt.PCA_SZ
        self.knn_K = opt.knn_K
        self.ball_radius2 = opt.ball_radius2
        self.sample_num_level1 = opt.sample_num_level1
        self.sample_num_level2 = opt.sample_num_level2
        self.INPUT_FEATURE_NUM = opt.INPUT_FEATURE_NUM
        
        self.netR_1 = nn.Sequential(
            # B*INPUT_FEATURE_NUM*sample_num_level1*knn_K
            nn.Conv2d(self.INPUT_FEATURE_NUM, nstates_plus_1[0], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_1[0]),
            nn.ReLU(inplace=True),
            # B*64*sample_num_level1*knn_K
            nn.Conv2d(nstates_plus_1[0], nstates_plus_1[1], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_1[1]),
            nn.ReLU(inplace=True),
            # B*64*sample_num_level1*knn_K
            nn.Conv2d(nstates_plus_1[1], nstates_plus_1[2], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_1[2]),
            nn.ReLU(inplace=True),
            # B*128*sample_num_level1*knn_K
            nn.MaxPool2d((1,self.knn_K),stride=1)
            # B*128*sample_num_level1*1
        )
        
        self.netR_2 = nn.Sequential(
            # B*131*sample_num_level2*knn_K
            nn.Conv2d(3+nstates_plus_1[2], nstates_plus_2[0], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_2[0]),
            nn.ReLU(inplace=True),
            # B*128*sample_num_level2*knn_K
            nn.Conv2d(nstates_plus_2[0], nstates_plus_2[1], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_2[1]),
            nn.ReLU(inplace=True),
            # B*128*sample_num_level2*knn_K
            nn.Conv2d(nstates_plus_2[1], nstates_plus_2[2], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_2[2]),
            nn.ReLU(inplace=True),
            # B*256*sample_num_level2*knn_K
            nn.MaxPool2d((1,self.knn_K),stride=1)
            # B*256*sample_num_level2*1
        )
        
        self.netR_3 = nn.Sequential(
            # B*259*sample_num_level2*1
            nn.Conv2d(3+nstates_plus_2[2], nstates_plus_3[0], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_3[0]),
            nn.ReLU(inplace=True),
            # B*256*sample_num_level2*1
            nn.Conv2d(nstates_plus_3[0], nstates_plus_3[1], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_3[1]),
            nn.ReLU(inplace=True),
            # B*512*sample_num_level2*1
            nn.Conv2d(nstates_plus_3[1], nstates_plus_3[2], kernel_size=(1, 1)),
            nn.BatchNorm2d(nstates_plus_3[2]),
            nn.ReLU(inplace=True),
            # B*1024*sample_num_level2*1
            nn.MaxPool2d((self.sample_num_level2,1),stride=1),
            # B*1024*1*1
        )
        
        self.netR_FC = nn.Sequential(
            # B*1024
            nn.Linear(nstates_plus_3[2], nstates_plus_3[3]),
            nn.BatchNorm1d(nstates_plus_3[3]),
            nn.ReLU(inplace=True),
            # B*1024
            nn.Linear(nstates_plus_3[3], nstates_plus_3[4]),
            nn.BatchNorm1d(nstates_plus_3[4]),
            nn.ReLU(inplace=True),
            # B*512
            nn.Linear(nstates_plus_3[4], self.num_outputs),
            # B*num_outputs
        )
    def forward(self, x, y):
        # x: B*INPUT_FEATURE_NUM*sample_num_level1*knn_K, y: B*3*sample_num_level1*1
        x = self.netR_1(x)
        # B*128*sample_num_level1*1
        x = torch.cat((y, x),1).squeeze(-1)
        # B*(3+128)*sample_num_level1
        
        inputs_level2, inputs_level2_center = group_points_2(x, self.sample_num_level1, self.sample_num_level2, self.knn_K, self.ball_radius2)
        # B*131*sample_num_level2*knn_K, B*3*sample_num_level2*1
        
        # B*131*sample_num_level2*knn_K
        x = self.netR_2(inputs_level2)
        # B*256*sample_num_level2*1
        x = torch.cat((inputs_level2_center, x),1)
        # B*259*sample_num_level2*1
        
        x = self.netR_3(x)
        # B*1024*1*1
        x = x.view(-1,nstates_plus_3[2])
        # B*1024
        x = self.netR_FC(x)
        # B*num_outputs
        
        return x

• 学习代码： https://github.com/erikwijmans/Pointnet2_PyTorch.git

level: CVPR, CCF_A
author:Pavlo Molchanov, Xiaodong Yang (NVIDIA)
date: 2016
keyword:

• Hand Gesture,

---

Paper: R3DCNN Dynamic Hand

Online Detection and Classification of Dynamic Hand Gestures with Recurrent 3D Convolutional Neural Networks

Proble Statement

• Large diversity in how people perform gestures.
• Work online to classify before competing a gesture.
• Three overlapping phases: preparation, nucleus, and retraction.

previous work:

• Hand-crafted spatio-temporal features.
  • Shape, appearance, motion cues( image gradients, optical flow).
• Feature representations by DNN.
  • uNeverova et al. combine color and depth data from hand regions and upper-body skeletons to recognize SL.
• Employ pre-segmented video sequences.
• Treate detect and classify separately

Methods

• Problem Formulation:

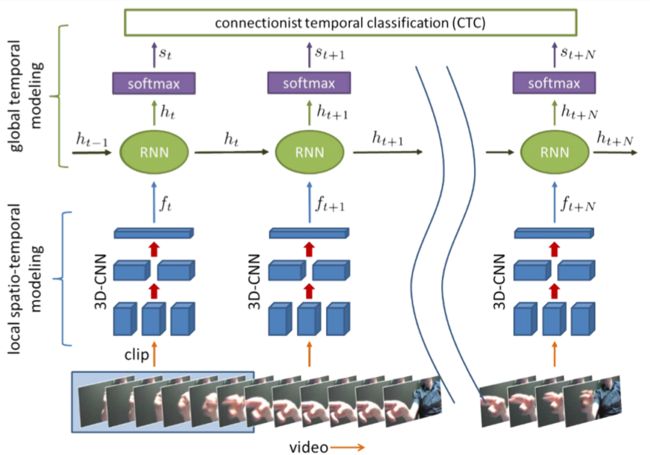
Input: a video clip as volume $C_t$: $C_tϵR^{k\ast l\ast c\ast m}$; $m$: sequential frames; $C$: channels of size $k\ast l$ pixels.

$h_tϵR_d$: a hidden state vector;

$W_{in}ϵR^{d\ast q}$, $W_hϵR^{d\ast d}$,$W_sϵR^{w\ast d}$: weight matrices;

$bϵR^w$: bias;

$S$: softmax functions, $R^w->R_{[0,1]}^w,where[S(x){]}_i=e^{x_i}/{\sum }_k{e}^{xk}$
$$\begin{gathered} F:R^{k\ast l\ast c\ast m}->R_q,where{f}_t=F(C_t) \\ {h}_t=R(W_{in}{f}_t+W_h{h}_{t-1}); \\ {s}_t=S(W_s{h}_t+b); \end{gathered}$$
For a video $V$ of $T$ clips, get the probabilities set $S$:
$$\begin{gathered} S=s_0,s_1,...,s_{T-1} \\ {S}^{avg}=1/T\sum _{sϵS}s \\ predicte{d}_{l}abel:y=argma{x}_i([s^{avg}{]}_i) \end{gathered}$$

• system overview:

【Pre-training the 3D-CNN】

• initialize the 3D-CNN with the C3D network [37] trained on the large-scale Sport1M [13] human action recognition dataset.
• append a softmax prediction layer to the last fully-connected layer and fine-tune by back-propagation with negative log-likelihood to predict gestures classes from individual clips $C_i$.

【Cost Function】

• For Log-likelihood cost function:

$$\begin{gathered} L_v=-1/P\sum _{i=0}^{P-1}log(p(y_i|V_i)) \\ p(y_i|V_i)=[s^{avg}{]}_{y_i} \end{gathered}$$

【Learning Rule】

• To optimize the network parameters $W$ with respect to either of the loss functions we use stochastic gradient descent (SGD) with a momentum term$\mu =0.9$. We update each parameter of the network θ ∈ W at every back-propagation step i by:

$$\begin{gathered} {\theta }_i={\theta }_{i-1}+v_i-yj{\theta }_{i-1} \\ {v}_i=u{v}_{i-1}-jJ(<\sigma E/\sigma \theta {>}_{batch}) \end{gathered}$$

Evaluation

• Environment:
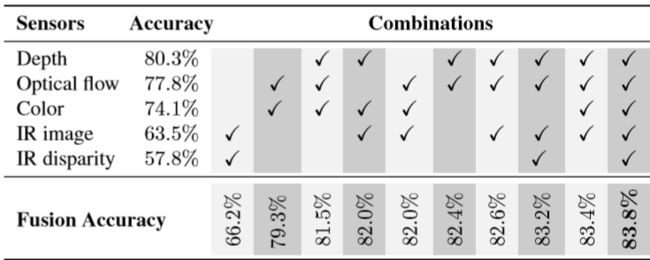
  • Dataset: used the SoftKinetic DS325 sensor to acquire frontview color and depth videos and a top-mounted DUO 3D sensor to record a pair of stereo-IR streams.
  • randomly split the data by subject into training (70%) and test (30%) sets, resulting in 1050 training and 482 test videos.
  • SKIG contains 1080 RGBD hand gesture sequences by 6 subjects collected with a Kinect sensor
  • ChaLearn 2014 dataset contains more than 13K RGBD videos of 20 upper-body Italian sign language gestures performed by 20 subjects
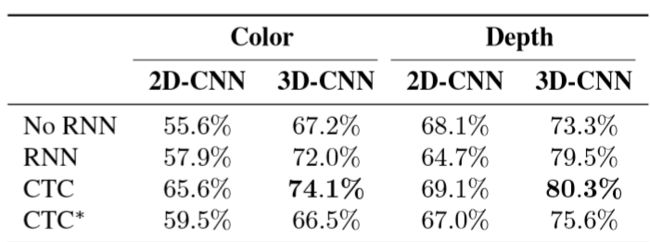
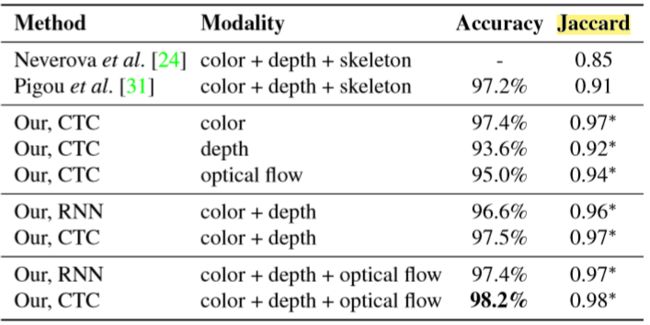
• Results:

Conclusion

• Design R3DCNN to performs simultaneous detection and classification.
• Using CTC model to predict label from in-progress gesture in unsegmented input streams.
• Achieves high accuracy of 88.4%.