NIN(Network In Network)

论文信息

论文名称：Network In Network
论文地址：https://arxiv.org/pdf/1312.4400.pdf
论文别名：NIN
发表期刊：ICLR（International Conference on Learning Representations）

摘要

我们提出了一种新式深度网络结构称之为NIN，增强模型对感受野内局部块的辨别力。 传统的卷积层使用线性过滤器后跟非线性激活函数来扫描输入。 与之相反的是我们构建更加复杂结构的微神经网络来使得感受野内的数据抽象化。 我们使用多层感知器来实例化微神经网络，这是一种强大的函数逼近器。 特征图是通过以与 CNN 类似的方式在输入上滑动微网络获得的，然后将特征图送入下一层。 深度 NIN 可以通过堆叠多个上述结构来实现。 通过微网络增强的局部建模，我们能够在分类层的特征图上利用全局平均池化，这比传统的全连接层更容易解释并且更不容易过拟合。同时我们展示了 NIN 在 CIFAR-10 和 CIFAR-100 上的最新分类性能，以及在 SVHN 和 MNIST 数据集上的合理性能。

批注

总感觉本文的作者对多层感知机有一些误解

主要工作

1. MLPCONV结构

NIN中mlpconv结构是将多层感知机MLP和卷积Conv集合在了一起，即传统卷积层Conv后加MLP层，构成NIN块，但在真正代码实现的时候作者用的是1x1的Conv，这点让我感觉很困惑，特意查了一下。

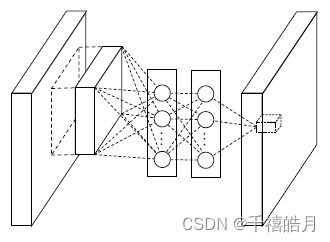
1.1为什么1×1卷积层可以代替MLP层

MLP层等价于全连接层。

当输入的特征图的尺寸为$n_c$x1x1时，全连接层和1X1的卷积层没有区别。

当输入为c×wxh时，卷积层和全连接层就不一样了，1×1的卷积输出为n×w×h,全连接的输出是n×1×1。此时，全连接可以等价于n个cxwxh卷积核的卷积层。全连接层和卷积层最大的区别就是输入尺寸是否可变，全连接层的输入尺寸是固定的，卷积层的输入尺寸是任意的。

1.2 批注

我到现在都没有明白作者为什么不在论文里写1x1卷积，非要搞出个MLPConv的概念.

2. Global Average Pooling(GAP)

在最后一个mlpconv层中为分类任务的每个对应类别生成一个特征图，通过GAP层取每个特征图的空间平均值，将结果向量直接传入到softmax层。（传统的做法都是在最后一层卷积层得到的特征图后面跟上FC层）

GAP较FC的优点：
①强制特征图和类别之间的对应关系，更适合卷积结构。
②GAP中没有要优化的参数，减少了参数量，避免了过拟合
③GAP汇总了空间信息，对输入的空间转化更加稳定。
④FC输入的大小必须固定，而GAP对网络输入的图像尺寸没有固定要求。
在使用 GAP 时 feature map 数要等于要分类的类别数，然后再对每一个 feature map 求均值，送到softmax中。

3、NIN网络结构

这篇文章中整个NIN网络包括：三个堆叠的mlpconv层和一个全局平均池化(GAP)层，如下图所示：
1、在三个mlpconv层后跟GAP。
2、可以在mlpconv层中间加入下采样层（与CNN和maxout网络一样）。
3、每个mlpconv层都有一个三层感知机。
4、NIN和微网络中的层数可根据特定任务调整。

NIN论文解读及个人理解

1、本文实际的NIN块(即mlpconv层)等价于普通卷积后跟两个1×1conv(即mlp层)，其中每个卷积操作后面都有ReLU进行非线性激活。

2、mlpconv的作用总结：
①相当于在通道间做特征融合。
②相当于每一层卷积之后加一个激活函数，增加了结构的非线性表达能力。

3、可以将与mlp等价的1×1conv+ReLU灵活运用到其他网络中（如GoogLeNet中的InceptionV1模块），后面的网络运用mlpconv时直接将之转化为1×1conv+ReLU。

4、1×1卷积思想：
①可以将1×1卷积看作是全连接层（将通道看成特征维，将宽和高维度上的样本当作是数据样本）
②1×1卷积既可以增加、减少通道数，也可以使通道数量不变化。

5、GAP思想：
① 前面的 mlpconv 层已经能提取出高维的有分类能力的特征了，不需要再多加几层FC层。可以把通道维看做特征维，宽度和长度的维度看做样本。那么 GAP 的本质就是把样本求均值映射到特征，因为最后一层的 feature map 数和类别数相同，那么也就是把样本映射到要分类的类别。

② FC层会综合前面卷积所提取所有的特征，可以把特征理解到更高的维度，来进行判别。也正是因为加上FC层，网络才更容易过拟合，因为FC层的理解力过于强大，它实际上是把所有可能考虑的情况都进行了考虑。怎么进行改进？因为我们前面用 mlpconv 层已经理解到了更高维能够分类的特征，那么最后就可以不用FC层，直接用 GAP 来对每个 feature map 求均值就行，因为模型已经把提取能够分类的特征的任务重心放到了整个模型的前面（mlpconv），后面只用综合前面的结果做出最后的判断就行。

NIN网络的代码实现（pytorch）
NiN块是NiN中的基础块。它由一个卷积层加两个充当全连接层的1×1卷积层(卷积层后跟ReLU)串联而成。其中第一个卷积层的超参数可以自行设置，而第二和第三个卷积层的超参数一般是固定的。

NIN网络的代码实现（pytorch）

NIN 块实现

import torch.nn as nn
import torch.nn.functional as F
class NIN_BLOCK(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride, padding):
        super(NIN_BLOCK, self).__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=1)
        self.conv3 = nn.Conv2d(out_channels, out_channels, kernel_size=1)
    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = self.conv3(x)
        return F.relu(x)

GAP层实现一

class GlobalAvgPool2d(nn.Module):
    # 全局平均池化层可通过将池化窗口形状设置成输入的高和宽实现
    def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
    def forward(self, x):
        return F.avg_pool2d(x, kernel_size=x.size()[2:])  

GAP层实现二

class GlobalAvgPool2d(nn.Module):
	def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
# nn.AdaptiveAvgPool2d(要转化成的大小)
## 如：
# nn.AdaptiveAvgPool2d((6, 6))
## 那么此函数会根据当前来到此处的 feature map 自动求 padding 和 stride，并输出（6,6）大小的 feature map
## 所以，此函数也能用到全卷积中，用来自动调整步长以适应图像不同的输入
		# 全局平均池化，就是如下写法：
		self.GAP = nn.AdaptiveAvgPool2d((1, 1))
	def forward(self, x):
		return self.GAP(x)

NIN 网络实现

class NIN(nn.Module):
    def __init__(self):
        super(NIN, self).__init__()
        self.block1 = NIN_BLOCK(3, 96, kernel_size=11, stride=4, padding=0)
        self.maxpool1 = nn.MaxPool2d(kernel_size=3, stride=2)  # 224*224*3 → 55*55*96 由以上两步共同完成
        self.block2 = NIN_BLOCK(96, 256, kernel_size=5, stride=1, padding=2)
        self.maxpool2 = nn.MaxPool2d(kernel_size=3, stride=2)  # 55*55*96 → 27*27*256
        self.block3 = NIN_BLOCK(256, 384, kernel_size=3, stride=1, padding=1)
        self.maxpool3 = nn.MaxPool2d(kernel_size=3, stride=2)  # 27*27*256 → 13*13*384
        self.block4 = NIN_BLOCK(384, 1000, kernel_size=3, stride=1, padding=1)
        self.GAP = GlobalAvgPool2d()
    def forward(self, x):
        x = self.block1(x)
        x = self.maxpool1(x)
        x = self.block2(x)
        x = self.maxpool2(x)
        x = self.block3(x)
        x = self.maxpool3(x)
        x = F.dropout(x, 0.5, training=self.training)
        x = self.block3(x)
        x = self.GAP(x)
        x = x.view(x.shape[0], -1)  # 将四维输出转换为二维输出，即形状为（批量大小，1000）
        return F.softmax(x, dim=1)

参考文献

https://www.jianshu.com/p/1690899f869e (对1x1卷积层和全连接层关系的解释）
https://blog.csdn.net/qq_40635082/article/details/123146987（NIN论文解读很到位）