【计算机图形学】课程设计——三维美术馆漫游

计算机图形学课程设计——三维美术馆漫游

一、实验目的

1. 掌握三维应用软件基本开发流程；
2. 掌握基本三维建模软件Blender的基本建模方法；
3. 掌握虚拟现实引擎WorldViz Vizard呈现三维场景的方法；
4. 掌握三维模型呈现软件Assimp预览三维模型的方法（验证三维模型文件）；

二、实验方法

2.1 钟表部分

2.1.1 设计三维钟表表盘、表针的主要步骤 & 截图

本钟表的设计主要包含：表盘、时针、分针、秒针。

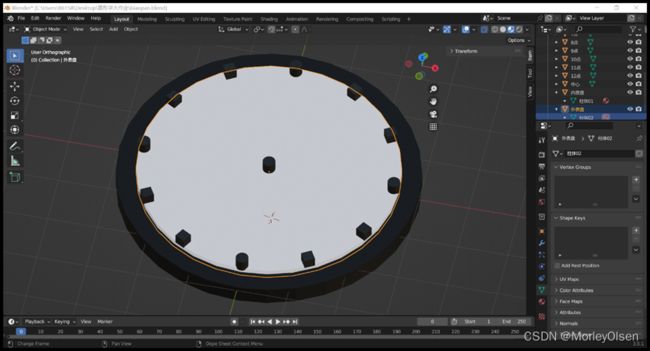
第一步，设计表盘。内盘的颜色为白色，外盘的颜色为黑色，刻度位置以正方体或圆柱体显示，其中0点、3点、6点、9点时刻为圆柱体，其他时刻为长方体，表盘中心连接表针处以圆柱体显示。同时，表盘中所有正方体或圆柱体均为黑色。圆柱体直接放置在内盘刻度表圆的边界位置，正方体则需要先放置在刻度表圆的边界位置，然后进行一定角度的旋转，以朝向表盘中心。

内盘和外盘的参数数据如下表所示：

表盘对象	X scale	Y scale	Z scale	X Location/m	Y Location/m	Z Location/m
内盘	2.6	2.6	0.1	0	0	0.1
外盘	3	3	0.2	0	0	-0.1

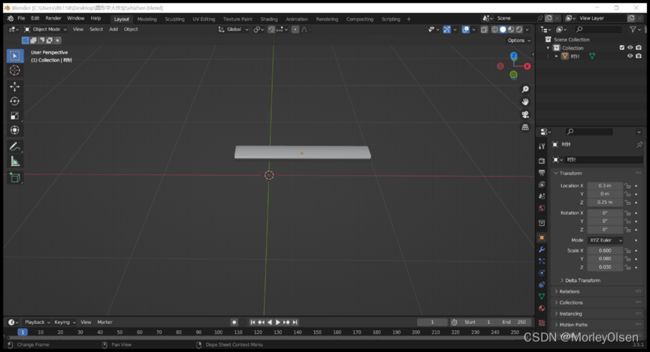
第二步，设计时针。时针的颜色为黑色，长度最短。时针端点处相对于钟表的圆心在钟表盘面上有一定偏移。

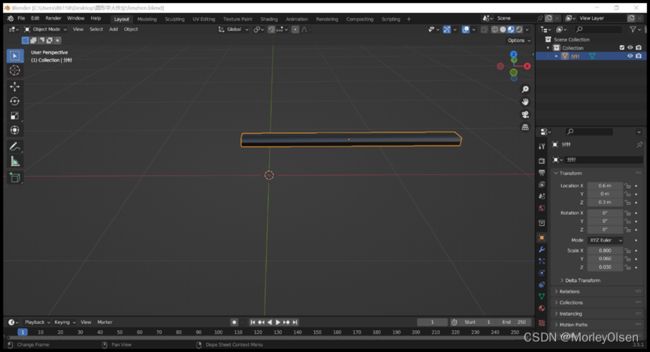
第三步，设计分针。分针的颜色为黑色，长度最长。分针端点处相对于钟表的圆心在钟表盘面上有一定偏移。

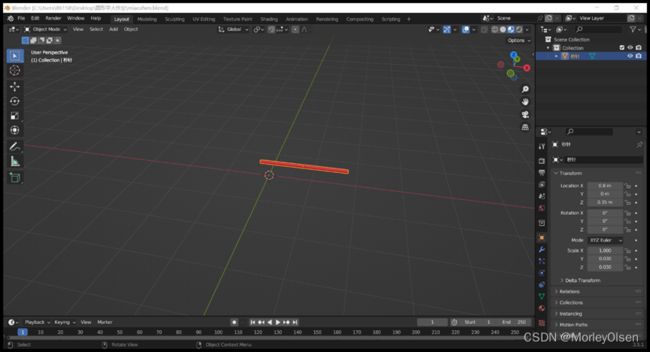
第四步，设计秒针。秒针的颜色为红色，长度其次，且宽度为分针的一半。秒针端点处相对于钟表的圆心在钟表盘面上有一定偏移。

时针、分针、秒针的参数数据如下表所示：

表针对象	X Location/m	Y Location/m	Z Location/m	X scale	Y scale	Z scale
时针	0.3	0	0.25	0.6	0.08	0.03
分针	0.6	0	0.3	0.8	0.06	0.03
秒针	0.8	0	0.35	1	0.03	0.03

最终设计效果图如下图所示：
表盘：

时针：

分针：

秒针：

 

2.1.2 钟表刻度放置位置及角度的计算公式

在本实验中，我们将刻度表圆的半径设置为2.5m。为了计算各时刻点的放置位置，我们以0点至6点的时刻点连线为二维平面的x坐标，以3点至9点的时刻点连线为二维平面的y坐标，表盘二维平面所设置的坐标系如下图所示（与文档水平方向平行的轴为x轴，与文档竖直方向平行的轴为y轴，与图片右上角的投影坐标一致）：

为了方便阐述确定刻度点坐标的方法，此处我们以1点的坐标为例。已知1点刻度点位于x轴顺时针旋转30°的方向上，因此其x坐标为r * cos(-30°)≈ 2.17，y坐标为r * sin(-30°) = -1.25。 

因此，放置刻度点的坐标计算公式如下所示（其中θ为刻度点与x轴正向的夹角，γ为正方体自身的Z旋转角）：

计算对象	坐标的计算公式
X坐标	x = r * cosθ
Y坐标	y = r * sinθ
正方体自身的Z旋转角	γ = θ mod 90°

根据上述公式所求得的刻度标识物体的参数数据如下表所示（由于高度位于表盘表面且始终不变，因此Z Location恒为0.3m）：

对象	X Location/m	Y Location/m	Z Location/m	X旋转角/°	Y旋转角/°	Z旋转角/°
0点	2.5	0	0.3	0	0	0
1点	2.17	-1.25	0.3	0	0	60
2点	1.25	-2.17	0.3	0	0	30
3点	0	-2.5	0.3	0	0	0
4点	-1.25	-2.17	0.3	0	0	60
5点	-2.17	-1.25	0.3	0	0	30
6点	-2.5	0	0.3	0	0	0
7点	-2.17	1.25	0.3	0	0	60
8点	-1.25	2.17	0.3	0	0	30
9点	0	2.5	0.3	0	0	0
10点	1.25	2.17	0.3	0	0	60
11点	2.17	1.25	0.3	0	0	30
中心	0	0	0.3	0	0	0

2.1.3 程序执行流程 & 钟表仿真截图
    在本实验中，我们首先通过localtime变量获取当前时刻的系统时间，然后通过setEuler函数分别修改时针、分针、秒针的角度，最后通过回调函数和定时器对时间进行刷新并控制钟表内时针、分针、秒针的角度显示。综上所述，程序执行流程如下图所示：

 

对应的程序代码如下所示：

# 时钟三维导入 # 表盘——plate、时针——hour、分针——minute、秒针——second # 设置初始的俯仰角为-90，blender模型为平放 plate = viz.add('biaopan.obj', pos=(0, 4.5, 9.9), euler=(0, -90, 0), scale=(0.3, 0.3, 0.3)) hour = viz.add('shizhen.obj', pos=(0, 4.5, 9.76), euler=(0, -90, 0), scale=(0.3, 0.3, 0.2))  minute = viz.add('fenzhen.obj', pos=(0, 4.5, 9.73), euler=(0, -90, 0), scale=(0.3, 0.3, 0.2)) second = viz.add('miaozhen.obj', pos=(0, 4.5, 9.7), euler=(0, -90, 0), scale=(0.3, 0.3, 0.2)) # 时钟控制 def clock():     # 获取当前系统时间     localtime = time.localtime()     # 时针角度设置     hour.setEuler(90, localtime.tm_hour * 30 + localtime.tm_min * 0.5 + localtime.tm_sec * 360 / 43200, 90)     # 分针角度设置     minute.setEuler(90, localtime.tm_min * 6 + localtime.tm_sec * 0.1, 90)     # 秒针角度设置     second.setEuler(90, localtime.tm_sec * 6, 90) # 时钟定时器 vizact.ontimer(0.5, clock) # 定时器回调函数 viz.callback(viz.MOUSE_MOVE_EVENT, onMouseMove)

在本实验中，我们通过viz.add()函数赋予plate、hour、minute、second四个变量所对应的obj文件的位置、欧拉角和规模。通过多次调试之后，我们发现钟表模型在以下数据下，可以展现出良好的姿态。

物体	位置坐标pos	欧拉角euler	模型规模scale
表盘plate	(0, 4.5, 9.9)	(0, -90, 0)	(0.3, 0.3, 0.3)
时针hour	(0, 4.5, 9.76)	(0, -90, 0)	(0.3, 0.3, 0.2)
分针minute	(0, 4.5, 9.73)	(0, -90, 0)	(0.3, 0.3, 0.2)
秒针second	(0, 4.5, 9.7)	(0, -90, 0)	(0.3, 0.3, 0.2)

其中，位置坐标是以（x，z，y）为标准进行设置。同时，由于在blender环境中，钟表的z坐标是朝上设置的，所以我们在虚拟引擎中需要将钟表的朝向进行修改，最终使得其在(0, -90, 0)的欧拉角下垂直悬挂在墙壁上。即，钟表放置的欧拉角公式为：

X角度	Y角度	Z角度
0°	0°	-90°

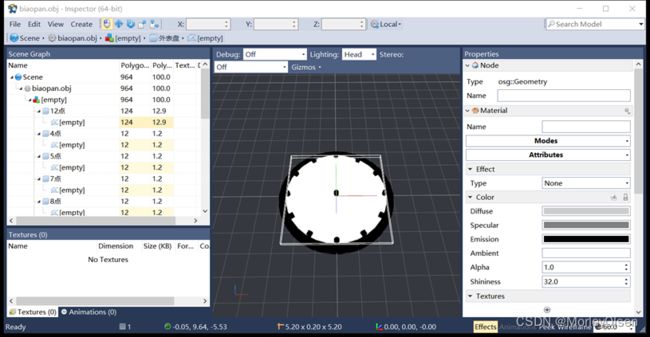
通过进入Inspector中，我们可以获得钟表各组成部件的仿真截图。最终结果如下图所示：
表盘：

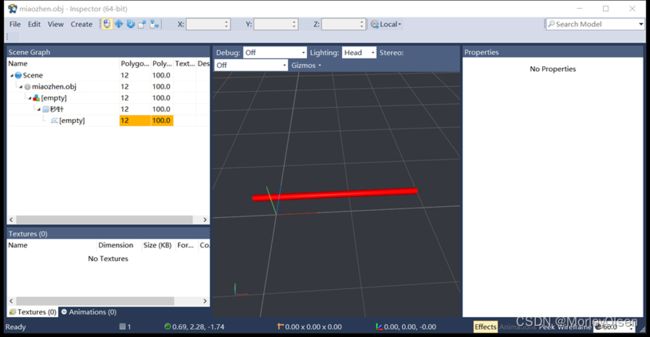
 秒针：

分针：

 时针：

2.1.4 表针旋转角度的计算公式 

根据实际钟表情况可知，秒针经过60秒旋转一周，分针经过60分钟（3600秒）旋转一周，时针经过12小时（43200秒）旋转一周。

秒针在一秒钟内更新360°/60 = 6°。

分针在一分钟内更新360°/60 = 6°，在一秒钟内更新360°/3600 = 0.1°。

时针在一小时内更新360°/12 = 30°，在一分钟内更新360°/720 = 0.5°，在一秒钟内更新360°/43200 ≈ 0.00833°。

因此，我们可以得到秒针、分针、时针的角度更新公式为：

计算对象	角度计算公式
秒针	θ= second * 6°
分针	θ= minute * 6° + second * 0.1°
时针	θ= hour * 30° + minute * 0.5° + second * 360°/43200

对应的程序代码如下所示：

# 时钟控制 def clock():     # 获取当前系统时间     localtime = time.localtime()     # 时针角度设置     hour.setEuler(90, localtime.tm_hour * 30 + localtime.tm_min * 0.5 + localtime.tm_sec * 360 / 43200, 90)     # 分针角度设置     minute.setEuler(90, localtime.tm_min * 6 + localtime.tm_sec * 0.1, 90)     # 秒针角度设置     second.setEuler(90, localtime.tm_sec * 6, 90)

2.1.5 表针相对于钟表圆心偏移的计算公式

    由于钟表的表针需要穿过圆心，因此可以人为设置超出圆心的距离。在本实验中，我们采取了以下数据进行表针的偏移：

计算对象	圆心偏移距离/m
秒针	1.0 - 0.8 = 0.2
分针	0.8 – 0.6 = 0.2
时针	0.6 – 0.3 = 0.3

在blender中，我们也可以查看到相关数据，其中location表示物体的中心位置，scale表示单侧的长度规模大小。查看结果如下图所示：
秒针：                                    

 

分针：

 时针：

 

2.2 人物部分

2.2.1 第三人称摄像机计算公式

人物与跟随相机之间的俯视位置关机如下图所示：

 

由上图可知，当人物自身进行逆时针旋转的时候，虚拟摄像机同样以人物为旋转参考点进行逆时针旋转。此时，鼠标的移动方向为视图左侧，而虚拟摄像机的移动方向为视图右侧，即二者的移动方向相反。在本实验中，我们将角度变化视为一个微小变量，近似将其等同为x方向上的位移长度。因此，第三人称摄像机各坐标参数的计算公式如下表所示：

计算对象	计算公式
θ	θ = dx / 10
X’	X’ = X – speed * sinθ
Y’	Y’ = Y
Z’	Z’ = Z – speed * cosθ

其中，θ为鼠标移动造成的旋转角，X、Y、Z为旋转前虚拟摄像机的三维坐标，X’、Y’、Z’为旋转后虚拟摄像机的三维坐标。

同时，为了限制Z坐标的变化使得视图与正常人体的视觉范围相同，我们将其约束在(-90°，90°)的范围。如果鼠标对应的旋转角超出该范围，则Z坐标不再改变。

因为人物在向前移动的时候，参考坐标系也在向前移动，因此摄像机的X坐标和Z坐标应该根据人物的speed适当减少。具体计算公式如下表所示：

计算对象	计算公式
X坐标减少量	speed * math.sin(math.pi * (e[0] / 180))
Z坐标减少量	speed * math.cos(math.pi * (e[0] / 180))

对应的程序代码如下所示：

# 摄像机 p = avatar.getPosition() e = avatar.getEuler() # 适当上移摄像机 p[1] = 2 p[2] -= R * math.cos(math.pi * (e[0] / 180)) p[0] -= R * math.sin(math.pi * (e[0] / 180)) e[1] += 10  # 初始状态适当俯视人物 view.setEuler(e) view.setPosition(p) # 视窗移动 def onMouseMove(m):     p = avatar.getPosition()     e = avatar.getEuler()     # 俯仰角     v = view.getEuler()[1] - m.dy / (speed * 10)     e[0] += m.dx / (speed * 5)     p[1] = 2     p[2] -= speed * math.cos(math.pi * (e[0] / 180))     p[0] -= speed * math.sin(math.pi * (e[0] / 180))     avatar.setEuler(e)     # 上下朝向的角度     if v > -90 and v < 90:         view.setEuler(e[0], v, e[2])     else:         view.setEuler(e)     view.setPosition(p)

2.2.2 利用键盘及鼠标实现前进、后退、左右跨步、左右旋转的原理

    在单位时间内，人物的移动距离与其移动速度的大小相等。将移动距离依据当前位置的旋转角度投影到坐标轴，即可得到X坐标、Y坐标、Z坐标在相应操作下的更新公式。

因此，X坐标、Y坐标、Z坐标在相应操作下的更新公式如下所示：

操作	X坐标更新公式	Y坐标更新公式	Z坐标更新公式
向前走	X’= X + speed * sinθ	Y’= Y	Z’= Z + speed * cosθ
向后走	X’= X - speed * sinθ	Y’= Y	Z’= Z - speed * cosθ
向左走	X’= X - speed * sin(θ+90°)	Y’= Y	Z’= Z - speed * cos(θ+90°)
向右走	X’= X - speed * sin(θ-90°)	Y’= Y	Z’= Z - speed * cos(θ-90°)

对应的程序代码如下所示：

# 人物移动 def UpdatePerson():     # 获取位置     p = avatar.getPosition()     # 获取角度     Euler = avatar.getEuler()     # 用户无操作，站立     if not (viz.key.isDown('w') or viz.key.isDown('a') or viz.key.isDown('d') or viz.key.isDown('s') or viz.key.isDown('r') or viz.key.isDown('e')):         avatar.state(1)     # w——前进     elif viz.key.isDown('w'):         p[2] += mvspeed * math.cos(math.pi * (Euler[0] / 180))         p[0] += mvspeed * math.sin(math.pi * (Euler[0] / 180))         avatar.setPosition(p)         avatar.state(2)     # s——后退     elif viz.key.isDown('s'):         p[2] -= mvspeed * math.cos(math.pi * (Euler[0] / 180))         p[0] -= mvspeed * math.sin(math.pi * (Euler[0] / 180))         avatar.setPosition(p)         avatar.state(2)     # a——左走     elif viz.key.isDown('a'):         p[2] -= mvspeed * math.cos(math.pi * (Euler[0] / 180) + 90)         p[0] -= mvspeed * math.sin(math.pi * (Euler[0] / 180) + 90)         avatar.setPosition(p)         avatar.state(12)     # d——右走     elif viz.key.isDown('d'):         p[2] -= mvspeed * math.cos(math.pi * (Euler[0] / 180) - 90)         p[0] -= mvspeed * math.sin(math.pi * (Euler[0] / 180) - 90)         avatar.setPosition(p)         avatar.state(13)     # t——向前跑     elif viz.key.isDown('r'):         p[2] += mvspeed * math.cos(math.pi * (Euler[0] / 180)) * 2         p[0] += mvspeed * math.sin(math.pi * (Euler[0] / 180)) * 2         avatar.setPosition(p)         avatar.state(11)     # e——蹲下     elif viz.key.isDown('e'):         avatar.state(10)     # 更新摄像机位置     p[1] = 2     p[0] -= R * math.sin(math.pi * (Euler[0] / 180))     p[2] -= R * math.cos(math.pi * (Euler[0] / 180))     view.setPosition(p)

2.2.3 人物行走过程中实现行走动画的程序逻辑

    人物在行走过程中的位置更新，与摄像机位置的更新类似。因此，我们只需要将摄像机位置的更新同步给人物，同时调用相关state为漫游动画，即可完成人物的行走模拟。其程序逻辑如下图所示：

 

三、实验结果

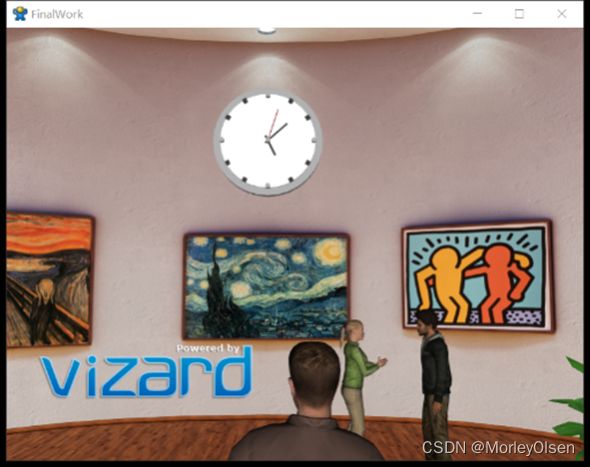
3.1 时钟实时显示当前系统时间
    本功能的最终实现结果如下图所示：

 

3.2 两个带动画的谈话小人

在本实验中，我们设置两个对象（male和female），通过viz.addAvatar()函数加载vcc_male2.cfg和vcc_female.cfg人物模型源文件，并设置pos和euler来控制男人和女人的欧拉角。其中，男人的欧拉角为(-90, 0, 0)，女人的欧拉角为(90, 0, 0)。因此，男人初始时面朝主角左侧，女人初始时面朝主角右侧。由于需要将男人和女人设置为谈话状态，因此需要将male.state和female.state进行相应赋值，此处我们将二者均赋值为4。

本功能的最终实现结果如下图所示：

 

对应的程序代码如下所示：

# 聊天的男人和女人 male = viz.addAvatar('vcc_male2.cfg', pos=(2, 0, 7), euler=(-90, 0, 0)) female = viz.addAvatar('vcc_female.cfg', pos=(1, 0, 7), euler=(90, 0, 0)) # 设置聊天动作 male.state(4) female.state(4)

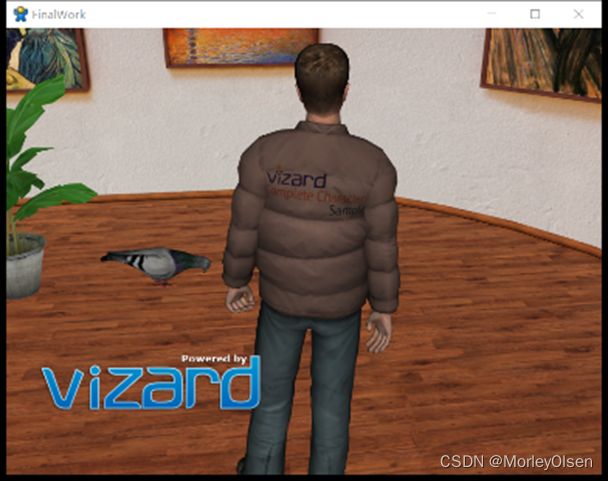
3.3 带动画的第三人称漫游

在本实验中，用户可以操作键盘和鼠标控制人物的移动和行为，具体漫游动画对应关系如下表所示：

用户操作	漫游动画
W	向前走
S	向后走
A	向左走
D	向右走
R	向前跑
E	蹲下观察

    由于截图无法完整展示动态过程，因此我们录制了一段带动画的第三人称漫游视频，完整地展示了上述操作和动画。详情请见video.mkv文件。

3.4 其他三维物体

    在本实验中，我们在原有场景下新增了两只鸽子、四个盆栽、一个天空盒。其中，一只鸽子位于谈话男生和谈话女生附近，执行漫步动作；另外一只鸽子位于初始化场景左侧的椅子附近，执行啄食动作；四个盆栽位于两个椅子的短边两侧附近；天空盒位于室内场景的天花板处。

3.4.1 鸽子

①漫步鸽子

本功能的最终实现结果如下图所示：

 
对应的程序代码如下所示：

# 鸽子1 bp = (0, 0, 6) bird = viz.addAvatar('pigeon.cfg', pos=bp, euler=(0, 0, 0), scale=(2, 2, 2)) # 设置移动函数 def birdMove():     p = list(bp)     p[0] += random.randint(-1, 1)     p[2] += random.randint(-1, 1) bird.addAction(vizact.walkTo(p)) # 鸟定时器 vizact.ontimer(1, birdMove) # 定时器回调函数 viz.callback(viz.MOUSE_MOVE_EVENT, onMouseMove)

②啄食鸽子

本功能的最终实现结果如下图所示：

 

对应的程序代码如下所示：

# 鸽子2 bp2 = (-3, 0, 6) bird2 = viz.addAvatar('pigeon.cfg', pos=bp2, euler=(0, 0, 0), scale=(2, 2, 2)) # 设置动作 bird2.state(3)

3.4.2 盆栽

①初始化场景左侧的椅子处的盆栽

本功能的最终实现结果如下图所示：

②初始化场景右侧的椅子处的盆栽

本功能的最终实现结果如下图所示：

 

对应的程序代码如下所示：

# 盆栽 plant1 = viz.addChild('plant.osgb', pos=(3, 0, 5)) plant2 = viz.addChild('plant.osgb', pos=(-3, 0, 5)) plant3 = viz.addChild('plant.osgb', pos=(-3, 0, 2)) plant4 = viz.addChild('plant.osgb', pos=(3, 0, 2))

3.4.3 天空盒

本功能的最终实现结果如下图所示：

 

对应的程序代码如下所示：

# 天空盒 sky = viz.addChild('sky_day.osgb')

---

python完整代码：

 walk-skeleton源代码：

import sys
import viz
import vizact
import vizinfo
import vizshape
import vizact
import math

speed = 2.0
view = viz.MainView

viz.setMultiSample(8)
viz.go()
viz.mouse.setVisible(viz.OFF) 

avatar = viz.addAvatar('vcc_male.cfg', pos=(0,0,0), euler=(0,0,0))
gallery = viz.add('gallery.osgb')

def UpdateView():
	m = viz.Matrix.euler(0,0,0)
	dm = viz.getFrameElapsed() * speed
	if viz.key.isDown('w'):
		m.preTrans([0,0,dm])
	if viz.key.isDown('s'):
		m.preTrans([0,0,-dm])
	if viz.key.isDown('a'):
		m.preTrans([-dm*0.3,0,0])
	if viz.key.isDown('d'):
		m.preTrans([dm*0.3,0,0])
	view.setEuler(m.getEuler())
	view.setPosition(m.getPosition(), viz.REL_PARENT)

vizact.ontimer(0,UpdateView)

修改后的漫游代码：

# 函数库使用
import sys
import viz
import vizact
import vizinfo
import vizshape
import vizact
import math
import random
import time

# 鼠标移动速度
speed = 2.0
# 人物移动速度
mvspeed = 0.03
# 相机和人物的相对位置
R = 2
# 主视角
view = viz.MainView
# 自动物品数目
viz.setMultiSample(8)
# 运行
viz.go()
# 隐藏鼠标光标
viz.mouse.setVisible(viz.OFF)

# 主角
avatar = viz.addAvatar('vcc_male.cfg', pos=(0, 0, 0), euler=(0, 0, 0))
# 美术馆
gallery = viz.add('gallery.osgb')
# 天空盒
sky = viz.addChild('sky_day.osgb')

# 聊天的男人和女人
male = viz.addAvatar('vcc_male2.cfg', pos=(2, 0, 7), euler=(-90, 0, 0))
female = viz.addAvatar('vcc_female.cfg', pos=(1, 0, 7), euler=(90, 0, 0))
# 设置聊天动作
male.state(4)
female.state(4)

# 鸽子1
bp = (0, 0, 6)
bird = viz.addAvatar('pigeon.cfg', pos=bp, euler=(0, 0, 0), scale=(2, 2, 2))


# 设置移动函数
def birdMove():
    p = list(bp)
    p[0] += random.randint(-1, 1)
    p[2] += random.randint(-1, 1)
    bird.addAction(vizact.walkTo(p))


# 鸽子2
bp2 = (-3, 0, 6)
bird2 = viz.addAvatar('pigeon.cfg', pos=bp2, euler=(0, 0, 0), scale=(2, 2, 2))
# 设置动作
bird2.state(3)

# 盆栽
plant1 = viz.addChild('plant.osgb', pos=(3, 0, 5))
plant2 = viz.addChild('plant.osgb', pos=(-3, 0, 5))
plant3 = viz.addChild('plant.osgb', pos=(-3, 0, 2))
plant4 = viz.addChild('plant.osgb', pos=(3, 0, 2))

# 摄像机
p = avatar.getPosition()
e = avatar.getEuler()
# 适当上移摄像机
p[1] = 2
p[2] -= R * math.cos(math.pi * (e[0] / 180))
p[0] -= R * math.sin(math.pi * (e[0] / 180))
e[1] += 10  # 初始状态适当俯视人物
view.setEuler(e)
view.setPosition(p)


# 视窗移动
def onMouseMove(m):
    p = avatar.getPosition()
    e = avatar.getEuler()
    # 俯仰角
    v = view.getEuler()[1] - m.dy / (speed * 10)
    e[0] += m.dx / (speed * 5)
    p[1] = 2
    p[2] -= speed * math.cos(math.pi * (e[0] / 180))
    p[0] -= speed * math.sin(math.pi * (e[0] / 180))
    avatar.setEuler(e)
    # 上下朝向的角度
    if v > -90 and v < 90:
        view.setEuler(e[0], v, e[2])
    else:
        view.setEuler(e)
    view.setPosition(p)


# 人物移动
def UpdatePerson():
    # 获取位置
    p = avatar.getPosition()
    # 获取角度
    Euler = avatar.getEuler()
    # 用户无操作，站立
    if not (viz.key.isDown('w') or viz.key.isDown('a') or viz.key.isDown('d') or viz.key.isDown('s') or viz.key.isDown('r') or viz.key.isDown('e')):
        avatar.state(1)
    # w——前进
    elif viz.key.isDown('w'):
        p[2] += mvspeed * math.cos(math.pi * (Euler[0] / 180))
        p[0] += mvspeed * math.sin(math.pi * (Euler[0] / 180))
        avatar.setPosition(p)
        avatar.state(2)
    # s——后退
    elif viz.key.isDown('s'):
        p[2] -= mvspeed * math.cos(math.pi * (Euler[0] / 180))
        p[0] -= mvspeed * math.sin(math.pi * (Euler[0] / 180))
        avatar.setPosition(p)
        avatar.state(2)
    # a——左走
    elif viz.key.isDown('a'):
        p[2] -= mvspeed * math.cos(math.pi * (Euler[0] / 180) + 90)
        p[0] -= mvspeed * math.sin(math.pi * (Euler[0] / 180) + 90)
        avatar.setPosition(p)
        avatar.state(12)
    # d——右走
    elif viz.key.isDown('d'):
        p[2] -= mvspeed * math.cos(math.pi * (Euler[0] / 180) - 90)
        p[0] -= mvspeed * math.sin(math.pi * (Euler[0] / 180) - 90)
        avatar.setPosition(p)
        avatar.state(13)
    # t——向前跑
    elif viz.key.isDown('r'):
        p[2] += mvspeed * math.cos(math.pi * (Euler[0] / 180)) * 2
        p[0] += mvspeed * math.sin(math.pi * (Euler[0] / 180)) * 2
        avatar.setPosition(p)
        avatar.state(11)
    # e——蹲下
    elif viz.key.isDown('e'):
        avatar.state(10)
    # 更新摄像机位置
    p[1] = 2
    p[0] -= R * math.sin(math.pi * (Euler[0] / 180))
    p[2] -= R * math.cos(math.pi * (Euler[0] / 180))
    view.setPosition(p)


# 时钟三维导入
# 表盘——plate、时针——hour、分针——minute、秒针——second
# 设置初始的俯仰角为-90，blender模型为平放
plate = viz.add('biaopan.obj', pos=(0, 4.5, 9.9), euler=(0, -90, 0), scale=(0.3, 0.3, 0.3))
hour = viz.add('shizhen.obj', pos=(0, 4.5, 9.76), euler=(0, -90, 0), scale=(0.3, 0.3, 0.2))  
minute = viz.add('fenzhen.obj', pos=(0, 4.5, 9.73), euler=(0, -90, 0), scale=(0.3, 0.3, 0.2))
second = viz.add('miaozhen.obj', pos=(0, 4.5, 9.7), euler=(0, -90, 0), scale=(0.3, 0.3, 0.2))


# 时钟控制
def clock():
    # 获取当前系统时间
    localtime = time.localtime()
    # 时针角度设置
    hour.setEuler(90, localtime.tm_hour * 30 + localtime.tm_min * 0.5 + localtime.tm_sec * 360 / 43200, 90)
    # 分针角度设置
    minute.setEuler(90, localtime.tm_min * 6 + localtime.tm_sec * 0.1, 90)
    # 秒针角度设置
    second.setEuler(90, localtime.tm_sec * 6, 90)


# 人物定时器
vizact.ontimer(0.01, UpdatePerson)
# 鸟定时器
vizact.ontimer(1, birdMove)
# 时钟定时器
vizact.ontimer(0.5, clock)
# 定时器回调函数
viz.callback(viz.MOUSE_MOVE_EVENT, onMouseMove)