23春-第三次集训题解

23春-第三次集训题解

L1-1 植树问题

某学校植树节开展植树活动，已知树苗有m株，参加植树的同学有n人（且m>n），请问每位同学平均可以植树几株？还有几株剩余？

输入格式:

输入两个整数m和n，分别表示树苗的数量和学生的人数（m>n）。

输出格式:

输出两个整数，分别表示每位同学平均植树的数量及剩余的树苗数量。

输入样例:

163 32

输出样例:

5 3

AC代码

#include 

using namespace std;

int m, n;

signed main() {
    cin >> m >> n;
    cout << m / n << ' ' << m % n;
    return 0;
}

L1-2 输出三角形面积和周长

本题要求编写程序，根据输入的三角形的三条边a、b、c，计算并输出面积和周长。注意：在一个三角形中， 任意两边之和大于第三边。三角形面积计算公式：
$$area=s(s-a)(s-b)(s-c)$$
其中
$$s=(a+b+c)/2$$

输入格式:

输入为3个正整数，分别代表三角形的3条边a、b、c。

输出格式:

如果输入的边能构成一个三角形，则在一行内，按照

area = 面积; perimeter = 周长

的格式输出，保留两位小数。否则，输出

These sides do not correspond to a valid triangle

输入样例1:

5 5 3

输出样例1:

area = 7.15; perimeter = 13.00

输入样例2:

1 4 1

输出样例2:

These sides do not correspond to a valid triangle

AC代码

#include 

using namespace std;

int a, b, c;

signed main() {
    cin >> a >> b >> c;
    double s = (a + b + c) / 2.0;
    double area = sqrt(s * (s - a) * (s - b) * (s - c));
    double p = a + b + c;
    if (a + b > c && b + c > a && a + c > b)
        printf("area = %.2f; perimeter = %.2f\n", area, p);
    else 
        printf("These sides do not correspond to a valid triangle");
    return 0;
}

L1-3 出租车计费问题

根据某城市普通出租车收费标准编写程序进行车费计算。具体标准如下：
起步里程为3公里，起步费10元；
超起步里程部分且10公里内，每公里2元；
超过10公里以上的部分加收50%的回空补贴费，即每公里3元。
如果输入值为负数，则输出“Input error!"

输入格式:

在一行中给出输入行驶里程（单位为公里）

输出格式:

在一行中输出乘客应支付的车费（单位为元），结果四舍五入，保留到元。

输入样例:

在这里给出一组输入。例如：

-1

输出样例:

在这里给出相应的输出。例如：

Input error!

输入样例:

在这里给出一组输入。例如：

2.6

输出样例:

在这里给出相应的输出。例如：

10

输入样例:

在这里给出一组输入。例如：

3

输出样例:

在这里给出相应的输出。例如：

10

输入样例:

在这里给出一组输入。例如：

9.8

输出样例:

在这里给出相应的输出。例如：

24

输入样例:

在这里给出一组输入。例如：

10

输出样例:

在这里给出相应的输出。例如：

24

输入样例:

在这里给出一组输入。例如：

12.2

输出样例:

在这里给出相应的输出。例如：

31

• 四舍五入%.0f即可

AC代码

#include 

using namespace std;

signed main() {
    double x;
    cin >> x;
    if (x < 0) {
        puts("Input error!");
    }
    else if (x <= 3) {
        cout << 10;
    }
    else if (x <= 10) {
        printf("%.0f\n", 10.0 + (x - 3) * 2.0);
    }
    else if (x > 10) {
        printf("%.0f\n", 10.0 + 7 * 2.0 + (x - 10) * 3.0);
    }
    return 0;
}

L1-4 判断回文

用户从键盘输入一个整数，程序将判断这个数是几位数并输出其位数，并判断这个数是否是回文数，是则输出Y，否则输出N。回文数是指将该数含有的数字逆序排列后得到的数和原数相同，例如12121、3223都是回文数。

输入格式:

整数

输出格式:

几位数
是否是回文数

输入样例:

在这里给出一组输入。例如：

12121

输出样例:

在这里给出相应的输出。例如：

5
Y

AC代码

#include 

using namespace std;

bool check(string s) {
    for (int i = 0; i < s.size() / 2; i++) {
        if (s[i] != s[s.size() - i - 1])
            return false;
    }
    return true;
}
// 直接反转判断
bool check1(string s) {
    string str = s;
    reverse(s.begin(), s.end());
    return str == s;
}

signed main() {
    string str;
    cin >> str;
    cout << str.size() << endl;
    cout << (check(str) ? "Y" : "N");
    return 0;
}

L1-5 百钱买百鸡问题 （枚举）

公鸡每只5元，母鸡每只3元，小鸡1元3只，而且鸡必须整只买。100元钱买100只鸡（每一种鸡都要有），公鸡、母鸡、小鸡各多少只？请编写程序给出各种购买方案。

输入格式:

输入为一个正整数n，表示要求输出前n种可能的方案。方案的顺序，是按照公鸡只数从少到多排列的。

输出格式:

显示前n种方案中公鸡、母鸡、小鸡各多少只。每行显示一种方案，数字之间空一格，最后一个数字后没有空格。

注意：如果全部方案不到n种，就顺序输出全部可能的方案。

输入样例:

在这里给出一组输入。例如：

5

输出样例:

在这里给出相应的输出。例如：

4 18 78
8 11 81
12 4 84

AC代码

#include 

using namespace std;

int n, cnt;

signed main() {
    cin >> n;
    for (int i = 1; i <= 20; i++) { //5
        for (int j = 1; j <= 33; j++) { // 3
            for (int k = 1; k <= 33; k++) {
                if (i * 5 + j * 3 + k == 100 && i + j + k * 3 == 100 && cnt < n)
                {
                    cout << i << ' ' << j << ' ' << k * 3 << endl;
                    cnt ++;
                }
            }
        }
    }
    return 0;
}

L1-6 h0018.金币（1）（思维）

国王以金币支付给他忠诚的骑士。在他服役的第一天，骑士会得到一枚金币。在接下来的每两天(服务的第二和第三天)，骑士会收到两枚金币。在在接下来的三天里(第四、第五和第六天)，骑士每一天都会得到三枚金币。在接下来的4天里(第七、第八、第九和第十天)，每一天骑士会得到4枚金币。这种支付模式将无限期地持续下去:在每个N在接下来的连续N+1天里，骑士将获得N+1个金币，其中N是任意正整数。请你编写程序将确定在任何给定的天数内支付给骑士的金币总数(从第一天开始)。

输入格式:

输入的每一行(最后一行除外)都包含问题的一个测试用例的数据，由精确的1个整数(取值范围1…10000)，表示天数。输入的结束以一行作为信号包含数字0。

输出格式:

每个测试用例只有一行输出。先输出相应的一行输入的天数，后面跟着一个空格和支付给骑士的金币总数在给定的天数内，从第一天开始。

输入样例:

10
6 
7
11
15
16
100
10000
1000
21
22
0

输出样例:

10 30
6 14
7 18
11 35
15 55
16 61
100 945
10000 942820
1000 29820
21 91
22 98

思路：

题意要求我们构造一个类似于
$$1，2，2，3，3，3，4，4，4，4，5，5，5，5，\mathrm{5......}$$
这样的数列，我们按题意预处理构造即可

同时注意最大天数为1e5 大概处理500个这样的数即可

AC代码：

#include 

#define pb push_back

using namespace std;

int n, x;

signed main() {
    vector v; v.pb(0);
    for (int i = 1; i <= 500; i++) {
        for (int j = 1; j <= i; j++)
            v.pb(i);
    }
    while (cin >> x, x) {
        cout << x << ' ';
        int res = 0;
        for (int i = 1; i <= x; i ++) res += v[i];
        cout << res << endl;
    }
    return 0;
}

L1-7 h0262. 求鞍点 （枚举）

给定一个 n×m 的整数矩阵，求矩阵中的所有鞍点。

鞍点，即该位置上的元素在该行上最大，在该列上最小。

有可能有多个鞍点，也可能没有鞍点。

输入格式:

第一行包含两个整数 n,m(1≤n,m<10)。

接下来 n 行，每行包含 m 个整数x(1≤x<10)。

输出格式:

输出所有鞍点的坐标和值。

输出优先级，整体从上到下，同行从左到右。

如果不存在鞍点，则输出 NO。

输入样例:

3 4
1 2 3 4
1 2 3 4
1 2 3 4

输出样例:

1 4 4
2 4 4
3 4 4

思路：

• 看题目数据量直接暴力即可
• 思路 ：遍历矩阵每个元素，判断当前元素所在的行列对应的最值是否相等，若相等则是鞍点，否则不是鞍点

AC代码

#include 

using namespace std;

const int N = 10 + 7， inf = 0x3f3f3f3f;

int n, m;
int g[N][N];

signed main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> g[i][j];
    bool f = false;
    for (int i = 1; i <= n; i++) 
    {
        for (int j = 1; j <= m; j++) 
        {
            int maxv = -1, minv = inf;
            for (int k = 1; k <= m; k++) {
                if (maxv <= g[i][k]) 
                    maxv = g[i][k];
            }
            for (int k = 1; k <= n; k++) {
                if (minv >= g[k][j]) 
                    minv = g[k][j];
            }
            if (maxv == minv)
            {
                f = true;
                cout << i << ' ' << j << ' ' << g[i][j] << endl;
            }
        }
    }
    if (!f) puts("NO");
    return 0;
}

L1-8 h0136. 在线翻译（字符串处理 or 二分）

您刚刚从毕节搬到了一个大城市。这里的人说的是一门不可理解的外语。幸运的是，您有一本字典可以帮助您理解它们。

输入格式:

输入最多包含100,000个字典条目，后跟一个空白行，然后是最多100,000个单词的消息。每个字典条目都是一行，包含英文单词，后跟一个空格和一个外语单词。在词典中，没有外来词出现多次。该消息是外语单词序列，每行一个单词。输入中的每个单词都是最多10个小写字母的序列。

输出格式:

输出是将消息翻译成英语，每行一个单词。词典中没有的外来词应翻译为“ eh”。

输入样例:

dog ogday
cat atcay
pig igpay
froot ootfray
loops oopslay

atcay
ittenkay
oopslay

输出样例:

cat
eh
loops

思路：

• 思路：开两个哈希表存映射关系
• 坑点：空行的处理，用getline读入整行，再分割出单词
• 分割单词的思路：我们可以用stringstream ，它会忽略空格读入；也可以用find找空格再截取出来

AC代码

#include 

using namespace std;

string str, a, b;
unordered_map st1, st2;

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    while (getline(cin, str) && str != "") {
        //int k = str.find(' ');
        //string a = str.substr(0, k), b = str.substr(k + 1);
        stringstream ss(str);
        ss >> a >> b;
        st1[a] = b, st2[b] = a;
    }
    while (cin >> str) {
        if (st1.count(str)) cout << st1[str] << endl;
        else if (st2.count(str)) cout << st2[str] << endl;
        else cout << "eh\n";
    }
    return 0;
}

L2-1 包装机 （栈模拟）

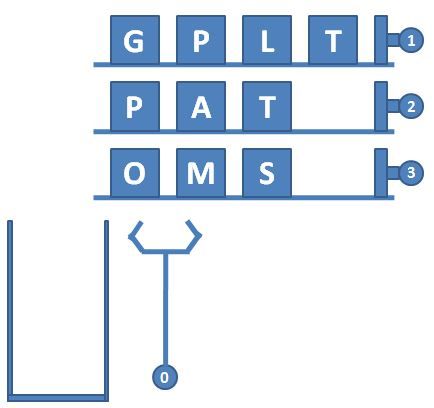
一种自动包装机的结构如图 1 所示。首先机器中有 N 条轨道，放置了一些物品。轨道下面有一个筐。当某条轨道的按钮被按下时，活塞向左推动，将轨道尽头的一件物品推落筐中。当 0 号按钮被按下时，机械手将抓取筐顶部的一件物品，放到流水线上。图 2 显示了顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态。

图1 自动包装机的结构

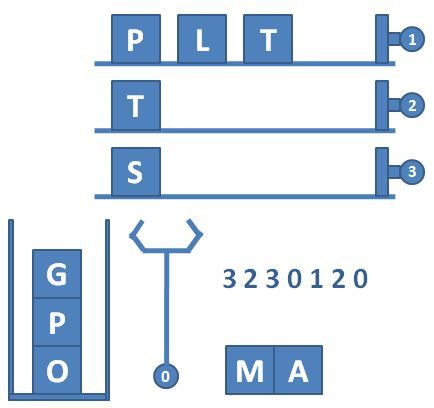
图 2 顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态

一种特殊情况是，因为筐的容量是有限的，当筐已经满了，但仍然有某条轨道的按钮被按下时，系统应强制启动 0 号键，先从筐里抓出一件物品，再将对应轨道的物品推落。此外，如果轨道已经空了，再按对应的按钮不会发生任何事；同样的，如果筐是空的，按 0 号按钮也不会发生任何事。

现给定一系列按钮操作，请你依次列出流水线上的物品。

输入格式：

输入第一行给出 3 个正整数 N（≤100）、M（≤1000）和 Smax（≤100），分别为轨道的条数（于是轨道从 1 到 N 编号）、每条轨道初始放置的物品数量、以及筐的最大容量。随后 N 行，每行给出 M 个英文大写字母，表示每条轨道的初始物品摆放。

最后一行给出一系列数字，顺序对应被按下的按钮编号，直到 −1 标志输入结束，这个数字不要处理。数字间以空格分隔。题目保证至少会取出一件物品放在流水线上。

输出格式：

在一行中顺序输出流水线上的物品，不得有任何空格。

输入样例：

3 4 4
GPLT
PATA
OMSA
3 2 3 0 1 2 0 2 2 0 -1

输出样例：

MATA

思路：

• 题意转化：给定一个栈和m个队列，栈容量不能超过题目限制，随后给出一系列字符串也就是m个队列，最后给出一系列操作数x， 当x == 0，时我们从取出栈顶（若当前栈非空）输出即可，当x != 0时，我们将对应编号的队列的队头取出放入栈顶，若此时栈满，我们先取出栈顶输出，再放入取出的队头。
• 思路：这里我开了个vector存各个队列，输入为了方便弹出尾部元素，反转了一下。也可以先直接通过front()取出队头，再erase()删除第一个元素。
• 坑点：注意判断栈满栈空的情况，以及各个队列为空的情况。

AC代码

#include 

using namespace std;

int x;
stack st;
vector v;

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int n, m, k;
    cin >> n >> m >> k;
    v.resize(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> v[i];
        //反转一下方便pop_back
        reverse(v[i].begin(), v[i].end()); 
    }
    while (cin >> x && x != -1) {
        if (x != 0 && !v[x].empty()) {
            if (st.size() == k) {
                cout << st.top();
                st.pop();
                st.push(v[x].back());
                v[x].pop_back();
            }
            else {
                st.push(v[x].back());
                v[x].pop_back();
            }
        }
        else if (x == 0) {
           if (st.size()) {
               cout << st.top();
               st.pop();
           }
        }
    }
    return 0;
}

L2-2 生肖统计（结构体排序）

春节至，亲朋好友聚会忙，聚会之人有时会说到自己的生肖。对于给定的若干人的生肖，请统计各种生肖的人数，并按人数从多到小输出各种出现的生肖及其人数。若有多种生肖的人数相同，则按生肖英文单词（详见最后的提示）的字典序输出。

输入格式:

首先输入一个正整数T，表示测试数据的组数，然后是T组测试数据。每组测试先输入1个整数n（1<=n<=100）表示聚会人数，再输入n个字符串（长度不超过7且仅包含小写字母），每个字符串表示一个人的生肖。

输出格式:

对于每组测试，按描述要求输出结果，每种出现的生肖及其人数占一行，每行的两个数据之间以一个空格间隔。每两组测试数据之间留一个空行。

输入样例:

2
4
tiger
rabbit
dragon
rabbit
5
tiger
rabbit
dragon
rabbit
dragon

输出样例:

rabbit 2
dragon 1
tiger 1

dragon 2
rabbit 2
tiger 1

提示:

鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪等十二生肖相应的英文单词如下：
rat、ox、tiger、rabbit、dragon、snake、horse、goat、monkey、rooster、dog、pig

思路：

• 结构体排序（水~）
• 注意题目要求的排序规则是人数优先，随后是按生肖单词字典序
• 按字典序排我们可以直接用string比较即可（因为string类重载了运算符）
• 排序时我们可以 写个cmp()函数 or 重载<都可

AC代码

#include 

using namespace std;
#define endl '\n'
#define pb push_back
const int N = 1000 + 7;

int n, t;

struct node {
    string a;
    int k;
    bool operator<(const node &o) const {
        if (k == o.k) return a < o.a;
        return k > o.k;
    }
};

signed main() {
    cin >> t;
    for (int i = 1; i <= t; i++) {
        cin >> n;
        unordered_map cnt;
        while (n--) {
            string str;
            cin >> str;
            cnt[str] ++;
        }
        vector ans;
        for (auto [k, v] : cnt) ans.pb({k, v});
        sort(ans.begin(), ans.end());
        for (auto [a, b] : ans) cout << a << ' ' << b << endl;
        if (i != t) cout << endl; 
    } 
    return 0;
}

L2-3 罪犯帮派（并查集）

Tabu市的警察局决定结束混乱，因此要采取行动根除城市中的几大帮派。目前的问题是，给出两个罪犯，他们是属于同一帮派么？城市里一共有多少个帮派？假设在Tabu市现有n名罪犯，编号为1到n，给出m条消息表示属于同一帮派的两个罪犯编号。请基于这些不完全的信息帮助警方计算出他们想要的信息。

输入格式:

输入第一行为三个正整数，n、m和q。n为罪犯数；m为给出的已知信息数量；q为查询数。接下来m行，每行2个正整数a和b，表示罪犯a和罪犯b属于同一帮派。接下来q行，每行2个正整数c和d，即查询罪犯c和d是否属于同一帮派。每行输入的整数以空格间隔，n、m、q均不超过1000。

输出格式:

输出为q+1行，前q行对应于输入的q个查询的结果，如果属于同一帮派，则输出“In the same gang.”，否则输出“In different gangs.”。最后一行为一个整数，表示帮派数目。

输入样例:

3 2 1
1 2
2 3
1 3

输出样例:

In the same gang.
1

• 并查集裸题（水~）

AC代码

#include 

using namespace std;

const int N = 1e3 + 7;

int n, m, q, cnt;
int p[N];

int find(int x) {
    if (x != p[x]) p[x] = find(p[x]);
    return p[x];
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++) p[i] = i;
    while (m --) {
        int a, b;
        cin >> a >> b;
        int fa = find(a), fb = find(b);
        if (fa != fb) p[fa] = fb;
    }
    while (q--) {
        int a, b;
        cin >> a >> b;
        if (find(a) == find(b)) cout << "In the same gang.\n";
        else cout << "In different gangs.\n";
    }
    int res = 0;
    for (int i = 1; i <= n; i++)
        if (p[i] == i)
            res ++;
    cout << res << endl;
    return 0;
}

L2-4 xt的考研路 （最短路）

xt是我院19级专业第一，但他认为保研并不能展示他全部的实力，所以他在22年初试一结束就加入了23考研的队伍中，并且他为了填补我院近些年来无北大研究生的空白，毅然决然决定扛起19级的大旗，在学校百年华诞之际献上他最诚挚的礼物。

xt每天都游走在寝室，食堂和图书馆，三点一线，即便是在疫情局势蔓延的形势下，凌晨三点半刚做完核酸，他六点半还是照常起来卷。现在他太忙了，好像在提前准备复试了，想让你帮个小忙，xt会给出学校的地图(有向图)，并且给出寝室，食堂和图书馆的编号(编号从0开始)，希望你从该图中找出一个子图，要使得在这个子图中，寝室能够到达图书馆，食堂也能到达图书馆，同时希望在这个子图中的所有边的边权之和最小。如果你找不到任何一个子图符合要求的话()，输出“xt,我好没本领！”，因为你找不到并不代表xt找不到

子图的定义：

从原图中删去一些点或删去一些线或既删去一些点又删去一些线，剩下的部分（当然必须仍然是图）。允许两种极端情况：什么都不删；删去所有点和所有线。

输入格式:

第一行输入点的个数 n，3 <= n <= 105，边的个数 m，0 <= m <= 2∗105

第二行给出寝室的编号id1，食堂的编号id2，图书馆的编号id3，题目保证三个编号两两不同。

随后 m 行按照以下形式描述边，表示有一条有向边，起点是from，终点是to，权值是w

from to w

0 <= from, to <= n - 1，from != to，1 <= w <= 109

输出格式1:

如果子图存在则输出最小边权和，如果不存在输出“xt,我好没本领！”

输入样例1:

6 9
0 1 5
0 2 2 
0 5 6 
1 0 3 
1 4 5 
2 1 1 
2 3 3 
2 3 4 
3 4 2 
4 5 1

输出样例1:

9

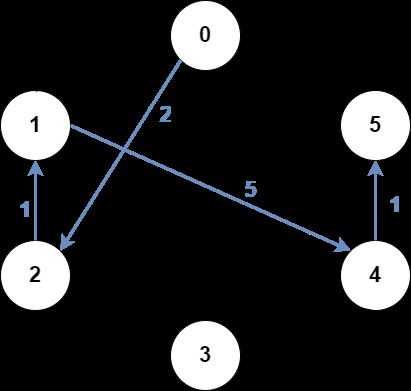
解释：

上图为输入的图。

蓝色边为最优子图之一。

注意，直接选择0 1 5三点构成的子图也能得到最优解，但无法在满足所有限制的前提下，得到更优解。

输入样例2:

3 2
0 1 2
0 1 1
2 1 1

输出样例2:

xt,我好没本领！

解释：

上图为输入的图。

可以看到，不存在从节点 1 到节点 2 的路径，所以不存在任何子图满足所有限制。

分析：

这题出在L2有点不太合理的，当时没看明白，感觉复杂就跳过了，现在一看还是需要点思维的，看了别人写的题解才懂了点思路。

题意：给定一个有向图，要求出一张子图，使得两个起点都能到达终点，且子图内的边权之和最小。

首先从边权之和最小我们自然而然地联系到最短路，从两个起点分别跑最短路，即起点1到终点，起点2到终点，但最终的答案可能并不是两条最短路简单相加(这种解法亲测13分)，因为中间可能会有重复部分，而我们要使得答案最小，就要使得重合的部分尽量的多，所以说直接跑两遍最短路再减去重复部分可能得不到最优解，因为二者的目的不同。

所以最终的子图应该是一个Y形，即两个起点到达某一个中间点，再一起从中间点到终点。

参考详解：xt的考研路

做法：

• 从起点1和起点2分别跑一遍dijkstra，并反向建图从终点跑一遍dijkstra，分别开dist数组记录最短路径
• 那么我们直接枚举中间点取最小值即可
• 注意开long long 题目会爆int，同时题目数据点数1e5边数2e5, 明显不能开二维数组，这里我们开邻接表（可以vector or 链式前向星）用堆优化djikstra算法
• 时间复杂度: $O(mlog(n))$

AC代码

#include

#define int long long
#define x first
#define y second

using namespace std;

typedef pair PII;
const int N = 1e5 + 7, inf = 0x3f3f3f3f;
int n, m, a, b, c, id1, id2, id3;
bool st[N];

vector dijkstra(vector > &g, int u) {
    vector dist(g.size());
    fill(dist.begin(), dist.end(), inf / 3);
    memset(st, false, sizeof st);
    dist[u] = 0;
    priority_queue, greater<>> heap;
    heap.emplace(0, u);
    while (!heap.empty()) {
        auto t = heap.top();
        heap.pop();
        int ver = t.y, distance = t.x;
        if (st[ver]) continue;
        st[ver] = true;
        for (auto v: g[ver]) {
            int j = v.x, w = v.y;
            if (distance + w < dist[j]) {
                dist[j] = distance + w;
                heap.emplace(dist[j], j);
            }
        }
    }
    return dist;
}

signed main() {
    cin.tie(nullptr)->ios::sync_with_stdio(false);
    cin >> n >> m;
    cin >> id1 >> id2 >> id3;
    vector > g(n), rg(n);
    while (m--) {
        cin >> a >> b >> c;
        g[a].emplace_back(b, c);
        rg[b].emplace_back(a, c);
    }
    auto dist1 = dijkstra(g, id1);
    auto dist2 = dijkstra(g, id2);
    auto dist3 = dijkstra(rg, id3);
    int res = inf;
    for (int i = 0; i < n; i++) {
        res = min(res, dist1[i] + dist2[i] + dist3[i]);
    }
    if (res < inf / 3) {
        cout << res << endl;
    }
    else {
        cout << "xt,我好没本领！" << endl;
    }
    return 0;
}

L3-1 炸僵尸（宁波小学2017）（搜索）

输入格式:

第一行四个用空格隔开的正整数表示 N,M,X,Y，分别表示 N 行 M 列的地图，小星星起
始位置第 X 行，第 Y 列。
接下来 N 行 M 列用来描述地图上每个单元格，‘G’表示僵尸，‘#’表示墙体，只有‘.’
表示的单元格才是小星星能够正常行走，能够放置炸弹的单元格。（数据保证四面都是墙体，
也就是第 1 行、第 N 行、第 1 列、第 M 列肯定都是墙体）。

输出格式:

一个整数，最多能炸掉的僵尸数量。

输入样例:

13 13 4 2
#############
###..GG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.#.#
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.#G#
#GG.GGG#G.GG#
#############

输出样例:

10

【数据范围】

30%的数据，保证 N,M<14，并且小星星一定能够抵达最佳炸弹放置点
40%的数据，保证 N,M<14
70%的数据，保证 N,M<101
100%的数据，保证 N,M<2001
100%的数据，保证 X

思路：

• 思路：DFS or BFS搜索出所有能走到的点，再更新最大炸到僵尸数量即可
• DFS写法和BFS写法都在下面

AC代码：

#include 

#define x first
#define y second

using namespace std;

typedef pair PII;
const int N = 2e3 + 7;

int n, m, x, y, res;
char g[N][N];
bool st[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int count(int x, int y) {
    int cnt = 0;
    //判断左右
    for (int j = y - 1; j >= 1; j--) {
        if (g[x][j] == '#') break;
        if (g[x][j] == 'G') cnt ++;
    }
    for (int j = y + 1; j <= m; j++) {
        if (g[x][j] == '#') break;
        if (g[x][j] == 'G') cnt ++;
    }
    //判断上下
    for (int i = x + 1; i <= n; i++) {
        if (g[i][y] == '#') break;
        if (g[i][y] == 'G') cnt ++;
    }
    for (int i = x - 1; i >= 1; i--) {
        if (g[i][y] == '#') break;
        if (g[i][y] == 'G') cnt ++;
    }
    return cnt;
}

void bfs(int x, int y) { 
    queue q;
    q.emplace(x, y);
    st[x][y] = true;
    res = count(x, y);
    while (!q.empty()) {
        auto t = q.front(); 
        q.pop();
        for (int i = 0; i < 4; i++) {
            int a = t.x + dx[i], b = t.y+ dy[i];
            if (a < 1 || a > n || b < 1 || b > m ) continue; 
            if (g[a][b] == '#' || g[a][b] == 'G' || st[a][b]) continue;
            if (g[a][b] == '.')
            {
                int cnt = count(a, b);
                res = max(res, cnt);
                st[a][b] = true;
                q.emplace(a, b);
            }
        }
    }
}

void dfs(int x, int y) {
    if (g[x][y] == '.') 
        res = max(res, count(x, y));
    for (int i = 0; i < 4; i++) {
        int a = x + dx[i], b = y + dy[i];
        if (a >= 1 && a <= n && b >= 1 && b <= m && g[a][b] == '.' && !st[a][b]) {
            st[a][b] = true;
            dfs(a, b);
        }
    }
}

signed main() {
    cin >> n >> m >> x >> y;
    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++)
            cin >> g[i][j];
    
    //bfs(x, y);
    
    dfs(x, y);
    
    cout << res << endl;
    
    return 0;
}

L3-2 h0172. 方格取数 (DP)

链接：AcWing 1027. 方格取数

AC代码

/*
如何处理同一个格子不能被重复选择
只有在i1 + j1 = i2 + j2 时候两条路径的格子才可能重合
由摘花生的问题可以推出三维状态转移方程 :
    f[i1, k-i1, i2, k -i2] - > f[k, i1, i2]
f[k, i, j] 表示所有从(1,1)分别走到(i1, k - i1), (i2, k - i2)的路径的最大值
k表示两条路线当前走到的格子的横纵坐标之和  (k = i1 + j1 = i2 + j2)

难点：格子仅能取一次. 两个小朋友在同一个格子必有i1==i2,j1==j2,
    而后边状态限制同时走,所以当i1==i2时便走到同一格.
    判断(i1,j1),(i2,j2)是否是同一个格子,若是则仅需要加上一个权重,反之两个都需要
*/

#pragma GCC optimize(2)

#include 

using namespace std;

const int N = 15;
int n;
int g[N][N];
int f[2 * N][N][N];

signed main() {
    cin >> n;
    int a, b, w;
    while (cin >> a >> b >> w, a || b || w) g[a][b] = w;

    for (int k = 2; k <= n + n; k++) {
        for (int i1 = 1; i1 <= n; i1++) {
            for (int i2 = 1; i2 <= n; i2++) {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) { //防止越界
                    int t = g[i1][j1];
                    if (i1 != i2) t += g[i2][j2]; //不重合则两条路径都需要加权重
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1][i2] + t);
                }
            }
        }
    }
    cout << f[n + n][n][n];
    return 0;
}

L3-3 h0249.DNA （状压DP or 搜索）

暴搜解法

状压DP解法

题目出处