统计软件与数据分析Lesson16----pytorch基本知识及模型构建

0.上节回顾

CPU版本的torch安装： pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple

加载包

import numpy as np
from sklearn.linear_model import LinearRegression

import torch
import torch.optim as optim
import torch.nn as nn
from torchviz import make_dot
from plots_lesson16 import *

plots_lesson16.py下载
plots_lesson16.py下载
plots_lesson16.py下载

0.1 一元线性回归

$$y=b+wx+ϵ$$

数据生成

true_b = 1
true_w = 2
N = 100

# Data Generation
np.random.seed(42)
x = np.random.rand(N, 1)
epsilon = (.1 * np.random.randn(N, 1))
y = true_b + true_w * x + epsilon

数据处理

# Shuffles the indices
idx = np.arange(N)
np.random.shuffle(idx)

# Uses first 80 random indices for train
train_idx = idx[:int(N*.8)]
# Uses the remaining indices for validation
val_idx = idx[int(N*.8):]

# Generates train and validation sets
x_train, y_train = x[train_idx], y[train_idx]
x_val, y_val = x[val_idx], y[val_idx]

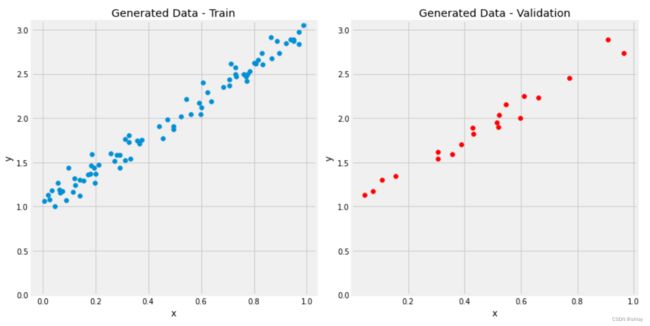
初始数据可视化

figure1(x_train, y_train, x_val, y_val)

0.2 梯度下降Gradient Descent

Step 0: 随机初始化 Random Initialization

# Step 0 - Initializes parameters "b" and "w" randomly
np.random.seed(42)
b = np.random.randn(1)
w = np.random.randn(1)

print(b, w)

[0.49671415] [-0.1382643]

Step 1: 计算模型预测值 Compute Model’s Predictions

# Step 1 - Computes our model's predicted output - forward pass
yhat = b + w * x_train

Step 2: 计算损失 Compute the Loss

# Step 2 - Computing the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error!
error = (yhat - y_train)

# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()

print(loss)

2.7421577700550976

Step 3: 计算梯度 Compute the Gradients

# Step 3 - Computes gradients for both "b" and "w" parameters
b_grad = 2 * error.mean()
w_grad = 2 * (x_train * error).mean()
print(b_grad, w_grad)

-3.044811379650508 -1.8337537171510832

Step 4: 参数更新 Update the Parameters

# Sets learning rate - this is "eta" ~ the "n" like Greek letter
lr = 0.1
print(b, w)

# Step 4 - Updates parameters using gradients and 
# the learning rate
b = b - lr * b_grad
w = w - lr * w_grad

print(b, w)

[0.49671415] [-0.1382643]
[0.80119529] [0.04511107]

Step 5: 重复迭代 Rinse and Repeat!

回到前面再次运行step1到step4 一直重复

step5:基于Numpy 的完整迭代code

# Step 0 - Initializes parameters "b" and "w" randomly
np.random.seed(42)
b = np.random.randn(1)
w = np.random.randn(1)

print(b, w)

# Sets learning rate 
lr = 0.1
# Defines number of epochs
n_epochs = 1000

for epoch in range(n_epochs):
    # Step 1 - Computes model's predicted output - forward pass
    yhat = b + w * x_train
    
    # Step 2 - Computes the loss
    # We are using ALL data points, so this is BATCH gradient descent.
    error = (yhat - y_train)
    # It is a regression, so it computes mean squared error (MSE)
    loss = (error ** 2).mean()
    
    # Step 3 - Computes gradients for both "b" and "w" parameters
    b_grad = 2 * error.mean()
    w_grad = 2 * (x_train * error).mean()
    
    # Step 4 - Updates parameters using gradients and the learning rate
    b = b - lr * b_grad
    w = w - lr * w_grad
    
print(b, w)

输出：
    [0.49671415] [-0.1382643]
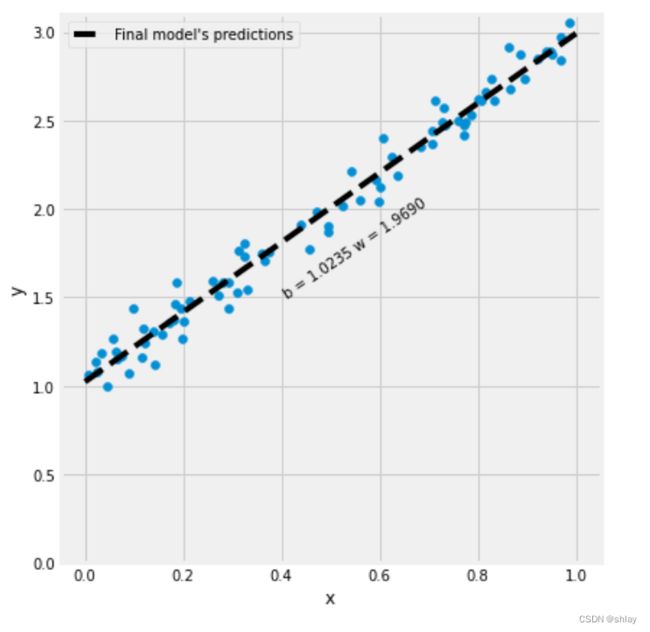
    [1.02354094] [1.96896411]

# Sanity Check: do we get the same results as our  gradient descent?
linr = LinearRegression()
linr.fit(x_train, y_train)
print(linr.intercept_, linr.coef_[0])

输出：
    [1.02354075] [1.96896447]

fig = figure3(x_train, y_train)

1. PyTorch

1.1 Tensor

1.1.1 概念定义

在Numpy中，你可能有一个具有三维空间的数组，对吧？从技术上来说，这就是一个张量。

A scalar (a single number) has zero dimensions, a vector has one dimension, a matrix has two dimensions, and a tensor has three or more dimensions. That’s it!

但是，为了简单起见，调用向量和矩阵张量也很常见——所以，从现在开始，所有的东西都是标量或张量。

PyTorch的张量与它的Numpy具有等价的函数，比如ones(), zeros(), rand(), randn()，等等。在下面的例子中，我们分别创建一个：标量、向量、矩阵和张量——或者，换句话说，是一个标量和三个张量。

scalar = torch.tensor(3.14159)
vector = torch.tensor([1, 2, 3])
matrix = torch.ones((2, 3), dtype=torch.float)
tensor = torch.randn((2, 3, 4), dtype=torch.float)

print(scalar)
print(vector)
print(matrix)
print(tensor)

输出：
    tensor(3.1416)
    tensor([1, 2, 3])
    tensor([[1., 1., 1.],
            [1., 1., 1.]])
    tensor([[[-0.4934,  0.2415, -1.1109,  0.0915],
             [-2.3169, -0.2168, -1.3847, -0.8712],
             [ 0.0780,  0.5258, -0.4880,  1.1914]],
    
            [[-0.8140, -0.7360, -0.8371, -0.9224],
             [-0.0635,  0.6756, -0.0978,  1.8446],
             [-1.1845,  1.3835, -1.2024,  0.7078]]])

You can get the shape of a tensor using its size() method or its shape attribute.

print(tensor.size(), tensor.shape)

输出：
    torch.Size([2, 3, 4]) torch.Size([2, 3, 4])

All tensors have shapes, but scalars have “empty” shapes, since they are dimensionless (or zero dimensions, if you prefer):

print(scalar.size(), scalar.shape)

输出：
    torch.Size([]) torch.Size([])

You can also reshape a tensor using its view() (preferred) or reshape() methods.

# We get a tensor with a different shape but it still is the SAME tensor
same_matrix = matrix.view(1, 6)
# If we change one of its elements...
same_matrix[0, 1] = 2.
# It changes both variables: matrix and same_matrix
print(matrix)
print(same_matrix)

输出：
    tensor([[1., 2., 1.],
            [1., 1., 1.]])
    tensor([[1., 2., 1., 1., 1., 1.]])

注意：view()方法只返回一个具有所需形状的张量，它与原始张量共享底层数据——它不会创建一个新的、独立的张量！ reshape()方法可能创建也可能不创建副本！正是因为这种明显奇怪的行为，所以对tensor进行形状变换时首选view()的原因。

# We can use "new_tensor" method to REALLY copy it into a new one
different_matrix = matrix.new_tensor(matrix.view(1, 6))
# Now, if we change one of its elements...
different_matrix[0, 1] = 3.
# The original tensor (matrix) is left untouched!
# But we get a "warning" from PyTorch telling us to use "clone()" instead!
print(matrix)
print(different_matrix)

输出：
    tensor([[1., 2., 1.],
            [1., 1., 1.]])
    tensor([[1., 3., 1., 1., 1., 1.]])

# Lets follow PyTorch's suggestion and use "clone" method
another_matrix = matrix.view(1, 6).clone().detach()
# Again, if we change one of its elements...
another_matrix[0, 1] = 4.
# The original tensor (matrix) is left untouched!
print(matrix)
print(another_matrix)

输出：
    tensor([[1., 2., 1.],
            [1., 1., 1.]])
    tensor([[1., 4., 1., 1., 1., 1.]])

1.1.2 数据加载、设备选择

将Numpy代码转换为PyTorch：从训练数据开始即x_train和y_train数组。 as_tensor()

x_train_tensor = torch.as_tensor(x_train)
x_train.dtype, x_train_tensor.dtype

输出：
    (dtype('float64'), torch.float64)

可以很容易地将其转换为一个不同的类型，比如一个较低精度（32位）的浮点数，它将占用更少的内存空间，使用.float()：

float_tensor = x_train_tensor.float()
float_tensor.dtype

输出：
    torch.float32

作为as_tensor()和from_numpy()都返回一个tensor，它与原始的Numpy数组共享底层数据,即修改原始的Numpy数组，也会相应修改PyTorch的tensor，反之亦然。

dummy_array = np.array([1, 2, 3])
dummy_tensor = torch.as_tensor(dummy_array)
# Modifies the numpy array
dummy_array[1] = 0
# Tensor gets modified too...
dummy_tensor

输出：
    tensor([1, 0, 3], dtype=torch.int32)

dummy_tensor.numpy()

输出：
    array([1, 0, 3])

定义 device

上面创建的都是CPU张量。这是什么意思？这意味着张量中的数据存储在计算机的CPU中，对其执行的任何操作都将由其CPU（中央处理单元）来处理，我们称这种张量为CPU张量。

另一种称为GPU张量。GPU（代表图形处理单元）是图形卡的处理器。这些张量将数据存储在显卡的内存中，在它们上面的操作由GPU执行。

device = 'cuda' if torch.cuda.is_available() else 'cpu'
device

输出：
    'cpu'

n_cudas = torch.cuda.device_count()
for i in range(n_cudas):
    print(torch.cuda.get_device_name(i))

gpu_tensor = torch.as_tensor(x_train).to(device)
gpu_tensor[0]

输出：
    tensor([0.7713], dtype=torch.float64)

加载数据到指定device

因此，我们定义了一个device，先将两个Numpy数组转换为PyTorch张量，再将它们转换为浮点数，最后将它们发送到device中。接下来看看此时的变量类型：

device = 'cuda' if torch.cuda.is_available() else 'cpu'

# Our data was in Numpy arrays, but we need to transform them 
# into PyTorch's Tensors and then we send them to the 
# chosen device
x_train_tensor = torch.as_tensor(x_train).float().to(device)
y_train_tensor = torch.as_tensor(y_train).float().to(device)

# Here we can see the difference - notice that .type() is more
# useful since it also tells us WHERE the tensor is (device)
print(type(x_train), type(x_train_tensor), x_train_tensor.type())

输出：
    <class 'numpy.ndarray'> <class 'torch.Tensor'> torch.FloatTensor

back_to_numpy = x_train_tensor.numpy()

back_to_numpy = x_train_tensor.cpu().numpy()

Can’t convert CUDA tensor to numpy. Use Tensor.cpu() to copy the tensor to host memory first.

1.1.3 创建参数

方法1

下面的代码块为我们创建了参数b和w的两个张量，包括梯度，但在默认情况下，它们是CPU张量。

# FIRST
# Initializes parameters "b" and "w" randomly, ALMOST as we
# did in Numpy since we want to apply gradient descent on
# these parameters we need to set REQUIRES_GRAD = TRUE
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, dtype=torch.float)
w = torch.randn(1, requires_grad=True, dtype=torch.float)
print(b, w)

输出：
    tensor([0.3367], requires_grad=True) tensor([0.1288], requires_grad=True)

相较于训练集或测试集的数据，参数需要计算其梯度，因此我们可以更新它们的值（即参数值的值）。这就是需要requires_grad=True,它告诉PyTorch计算梯度。

注意：永远不要忘记设置种子以确保reproducibility，就像我们之前在使用Numpy时所做的那样。PyTorch对应的随机种子设置方法是torch.manual_seed()。

在PyTorch和Numpy中使用相同的种子（如此处我们都是用的42），会得到相同的数字吗？

答案是否定的！

在相同的第三方包设置相同的随机种子才会得到相同的数字。PyTorch生成的数字序列与Numpy生成的序列不同，即使两个序列中使用的随机种子数值相同。即使都是pytorch在CPU和GPU上设置相同的种子得到的数据也不同。

方法2

如果下面的device为cuda GPU则会失去梯度设置

# SECOND
# But what if we want to run it on a GPU? We could just
# send them to device, right?
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
w = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
print(b, w)
# Sorry, but NO! The to(device) "shadows" the gradient...

输出：
    tensor([0.3367], requires_grad=True) tensor([0.1288], requires_grad=True)

方法3

若在GPU上创建参数。我们首先需要将tensor发送到device，然后使用requires_grad_()将其属性设置为True。

# THIRD
# We can either create regular tensors and send them to
# the device (as we did with our data)
torch.manual_seed(42)
b = torch.randn(1, dtype=torch.float).to(device)
w = torch.randn(1, dtype=torch.float).to(device)
# and THEN set them as requiring gradients...
b.requires_grad_()
w.requires_grad_()
print(b, w)

输出：
 tensor([0.3367], requires_grad=True) tensor([0.1288], requires_grad=True)

方法3可以成功地为参数b和w提供了需要梯度的GPU张量。但这样比较麻烦，下面的方法4是更为推荐的在GPU上创建参数的方法。

方法4

总是在device创建的时刻为其分配张量，以避免意外的行为！

# FINAL
# We can specify the device at the moment of creation
# RECOMMENDED!

# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)
print(b, w)

输出：
    tensor([0.3367], requires_grad=True) tensor([0.1288], requires_grad=True)

1.2 Autograd

pytorch自带求梯度的包，为我们省去了求偏导、链式法则等其它的一些复杂问题。

1.2.1 反向传播 backward

backward()的作用是告诉PyTorch计算所有数据加载时requires_grad=True的tensor对应的梯度。

# Step 1 - Computes our model's predicted output - forward pass
yhat = b + w * x_train_tensor

# Step 2 - Computes the loss
# We are using ALL data points, so this is BATCH gradient descent
# How wrong is our model? That's the error! 
error = (yhat - y_train_tensor)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()

# Step 3 - Computes gradients for both "b" and "w" parameters
# No more manual computation of gradients! 
# b_grad = 2 * error.mean()
# w_grad = 2 * (x_tensor * error).mean()
loss.backward()

新的“Step 3 Computes gradients for both “b” and “w” parameters”使用的是backward()

print(error.requires_grad, yhat.requires_grad, \
      b.requires_grad, w.requires_grad)
print(y_train_tensor.requires_grad, x_train_tensor.requires_grad)

输出：
    True True True True
    False False

1.2.2 grad

查看参数的具体梯度值

print(b.grad, w.grad)

输出：
    tensor([-3.1125]) tensor([-1.8156])

多次运行上面两个代码块，能看到梯度是累积的。另外，CPU和GPU上的输出会略有不同。

我们需要使用对应于当前损失的梯度来执行参数更新。而不应该使用累积的梯度。事实证明，这种行为可以用于规避硬件限制。

当我们的计算机内存不是很大时，我们还可以把一个mini-batch分成sub-mini-batches，计算这些“subs”的梯度，并累积它们，以得到与计算整个小批处理上的梯度相同的结果。

如果我们的内存能够处理的数据，不希望梯度累计怎么办呢？zero_()能够帮我们实现

# This code will be placed *after* Step 4
# (updating the parameters)
b.grad.zero_(), w.grad.zero_()

输出：
    (tensor([0.]), tensor([0.]))

1.2.3 参数更新 no_grad()

# Sets learning rate - this is "eta" ~ the "n"-like Greek letter
lr = 0.1

# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)

# Defines number of epochs
n_epochs = 1000

for epoch in range(n_epochs):
    yhat = b + w * x_train_tensor   
    error = (yhat - y_train_tensor)
    loss = (error ** 2).mean()
    loss.backward()
    with torch.no_grad():
        b -= lr * b.grad
        w -= lr * w.grad
    
    b.grad.zero_()
    w.grad.zero_()
    
print(b, w)

输出：
    tensor([1.0235], requires_grad=True) tensor([1.9690], requires_grad=True)

1.3 动态计算图 Dynamic Computation Graph

PyTorchViz包及其make_dot(variable)方法能让我们轻松地可视化与梯度计算相关联变量的Python变量图

# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)

# Step 1 - Computes our model's predicted output - forward pass
yhat = b + w * x_train_tensor

# Step 2 - Computes the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error! 
error = (yhat - y_train_tensor)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()

# We can try plotting the graph for any python variable: 
# yhat, error, loss...
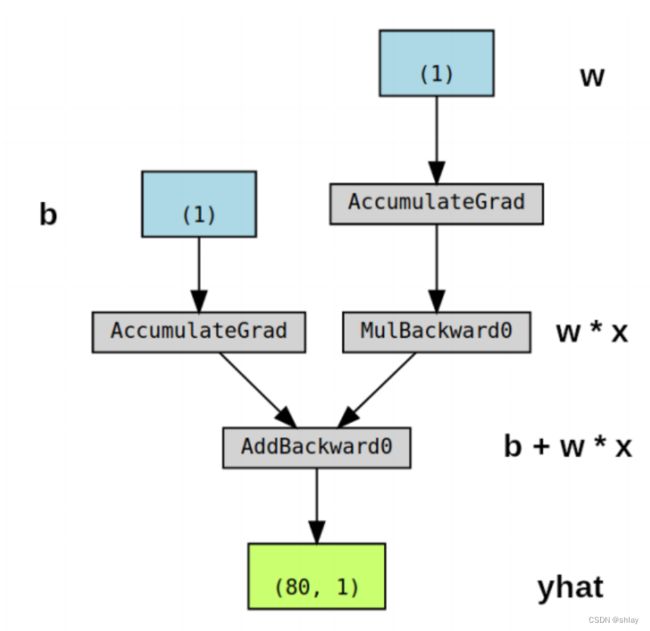
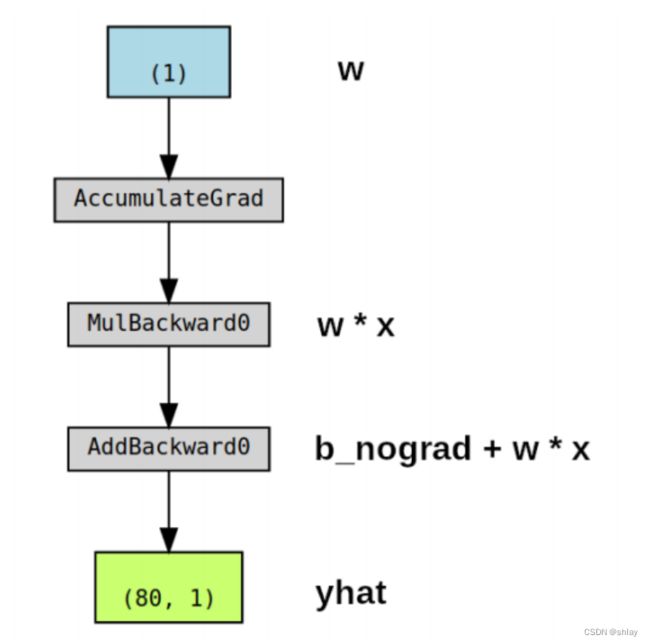
make_dot(yhat)

• 蓝框（(1)s）：对应于作为参数的张量，即要求PyTorch计算梯度的张量
• 灰框 (MulBackward0 和 AddBackward0):：涉及梯度计算张量或其依赖关系的Python操作
• 绿框 ((80, 1)):用作计算梯度起点的张量（假设 backward()方法从用于可视化图的变量调用）——它们是从图的自下而上计算的

便于理解,上图对应的变量标注如下所示：

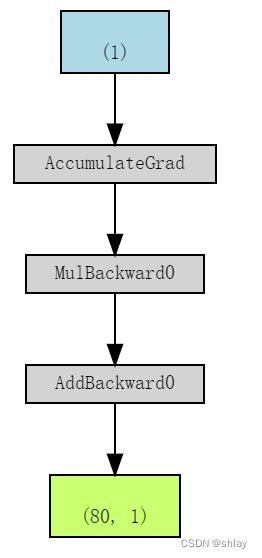
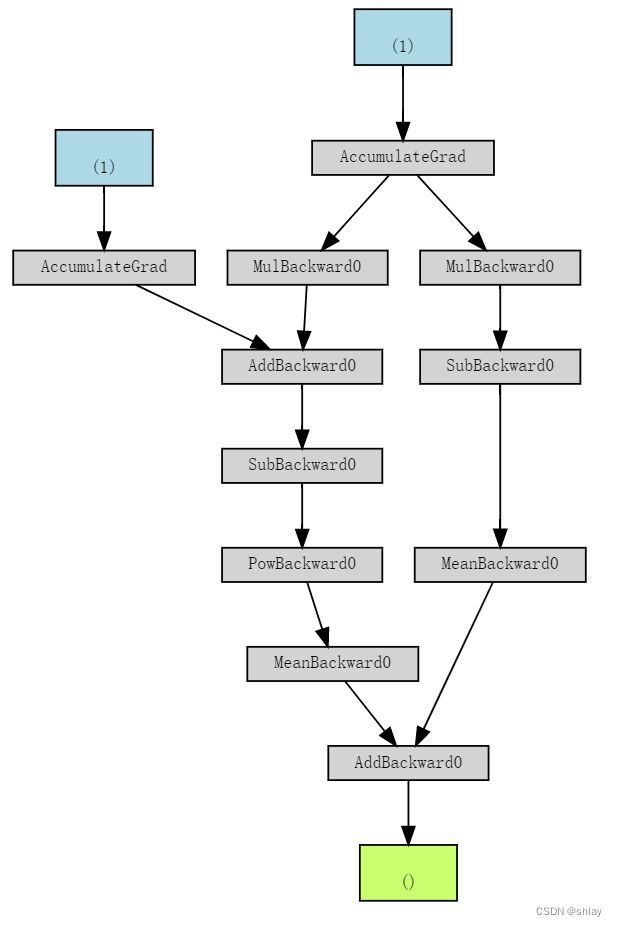
即使在计算图所执行的操作中涉及到更多的张量，它也只显示了梯度计算张量及其依赖关系。如果我们为参数b设置requires_grad=False，其对应的计算图如下所示：

b_nograd = torch.randn(1, requires_grad=False, \
                       dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)

yhat = b_nograd + w * x_train_tensor

make_dot(yhat)

Simple enough:** No gradients, no graph!**

关于动态计算图，最好的一点是，我们可以使它尽可能复杂。甚至可以使用控制流语句（例如，if语句）来控制梯度的流。

即使计算是荒谬的，我们也可以清楚地看到添加控制流语句的效果，如if loss > 0：它将计算图分支为两部分。右分支在if语句中执行计算，该语句最后被添加到左分支的结果中。很酷，对吧？尽管我们在这里没有构建更复杂的模型，但这个小例子很好地说明了PyTorch的功能，以及在代码中实现它们的难度。

b = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)

yhat = b + w * x_train_tensor
error = yhat - y_train_tensor
loss = (error ** 2).mean()

# this makes no sense!!
if loss > 0:
    yhat2 = w * x_train_tensor
    error2 = yhat2 - y_train_tensor
    
# neither does this :-)
loss += error2.mean()

make_dot(loss)

1.4 优化器 Optimizer

上面的例子中我们已经使用计算出的梯度手动更新参数。这对于两个参数来说可能还可以，但如果我们有很多参数呢？我们需要使用PyTorch的优化器，如SGD、RMSprop或Adam。

有许多优化器： 其中SGD是最基本的，而Adam是最受欢迎的之一。不同的优化器使用不同的机制来更新参数，但它们都通过不同的路径来实现相同的目标。

注意：mini-batch size的选择和Optimizer优化器的选择都会影响梯度下降的路径。

一个优化器的输入需要我们想要更新的参数，想要使用的学习速率（可能还有许多其他的超参数！），并通过optimizer.step()方法执行更新。

# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD([b, w], lr=lr)

# Sets learning rate - this is "eta" ~ the "n"-like Greek letter
lr = 0.1

# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)

# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD([b, w], lr=lr)

# Defines number of epochs
n_epochs = 1000

for epoch in range(n_epochs):
    yhat = b + w * x_train_tensor
   
    error = (yhat - y_train_tensor)

    loss = (error ** 2).mean()
    loss.backward()
    optimizer.step()
    optimizer.zero_grad()
    
print(b, w)

输出：
    tensor([1.0235], requires_grad=True) tensor([1.9690], requires_grad=True)

1.5 损失 Loss

pytorch中有许多损失函数可供选择。由于我们的是一元线性回归，所以使用均方误差（MSE）作为损失，即PyTorch的nn.MSELoss():

1.5.1 损失函数的定义和调用

# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')
loss_fn

输出：
    MSELoss()

# This is a random example to illustrate the loss function
predictions = torch.tensor([0.5, 1.0])
labels = torch.tensor([2.0, 1.3])
loss_fn(predictions, labels)

输出：
    tensor(1.1700)

1.5.2 包含loss的完整code

# Sets learning rate - this is "eta" ~ the "n"-like
# Greek letter
lr = 0.1

# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
                dtype=torch.float, device=device)

# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD([b, w], lr=lr)

# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')

# Defines number of epochs
n_epochs = 1000

for epoch in range(n_epochs):
    # Step 1 - Computes model's predicted output - forward pass
    yhat = b + w * x_train_tensor
    
    # Step 2 - Computes the loss
    loss = loss_fn(yhat, y_train_tensor)

    # Step 3 - Computes gradients for both "b" and "w" parameters
    loss.backward()
    
    # Step 4 - Updates parameters using gradients and the learning rate
    optimizer.step()
    optimizer.zero_grad()
    
print(b, w)

输出：
    tensor([1.0235], requires_grad=True) tensor([1.9690], requires_grad=True)

loss

输出：
    tensor(0.0080, grad_fn=<MseLossBackward0>)

如果想把loss作为一个Numpy数组呢？我们可以尝试再用一次numpy()，对吧？如果loss是在cuda设备中先用.cpu()。

loss.cpu().numpy()

输出：
    ---------------------------------------------------------------------------

    RuntimeError                              Traceback (most recent call last)

    <ipython-input-140-58c76a7bac74> in <module>()
    ----> 1 loss.cpu().numpy()
    

    RuntimeError: Can't call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.

报错了，这是因为loss tensor 实际上是在计算梯度与我们的数据张量不同，,为了使用numpy()，我们需要先用detach()将张量从计算图中分离出来：

loss.detach().cpu().numpy()

这样貌似有点麻烦，因为loss只有一个元素，所以可以使用item()或者tolist()来返回一个标量。

print(loss.item(), loss.tolist())

2. 模型 Model

在PyTorch中，模型由一个继承自模块类的常规Python类表示。一个 model class需要实现的最基本的方法是：

• 1.init(self):它定义了组成模型的部分——如上例中的两个参数b和w。
• 2.forward(self, x):执行实际计算；即给定输入x，输出一个预测值。

2.1 回归模型 LinearRegression

为上面的回归任务建立一个合适的（但也很简单的）模型。code如下：

2.1.1 定义 model class

class ManualLinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        # To make "b" and "w" real parameters of the model,
        # we need to wrap them with nn.Parameter
        self.b = nn.Parameter(torch.randn(1,
                                          requires_grad=True, 
                                          dtype=torch.float))
        self.w = nn.Parameter(torch.randn(1, 
                                          requires_grad=True,
                                          dtype=torch.float))
        
    def forward(self, x):
        # Computes the outputs / predictions
        return self.b + self.w * x

2.1.2 参数 Parameters

通过定义 model class，然后在__init__(self)中定义参数可以使用我们模型的parameters()方法来检索模型参数上的迭代器，包括嵌套模型的参数。然后可以使用它来feed我们的优化器（而不是自己构建一个参数列表！）。

torch.manual_seed(42)
# Creates a "dummy" instance of our ManualLinearRegression model
dummy = ManualLinearRegression()
list(dummy.parameters())

输出：
[Parameter containing:
 tensor([0.3367], requires_grad=True), Parameter containing:
 tensor([0.1288], requires_grad=True)]

2.1.3 状态字典 state_dict（）

此外，还可以利用模型的state_dict()方法得到所有参数的当前值。

dummy.state_dict()

输出：
OrderedDict([('b', tensor([0.3367])), ('w', tensor([0.1288]))])

optimizer.state_dict()

输出：
{'state': {0: {'momentum_buffer': None}, 1: {'momentum_buffer': None}},
 'param_groups': [{'lr': 0.1,
   'momentum': 0,
   'dampening': 0,
   'weight_decay': 0,
   'nesterov': False,
   'params': [0, 1]}]}

2.1.4 device

如果使用GPU，则需要把虚拟模型发送到设备上，如下所示：

torch.manual_seed(42)
# Creates a "dummy" instance of our ManualLinearRegression model
# and sends it to the device
dummy = ManualLinearRegression().to(device)

2.1.5 前向传播 Forward Pass

注意：您需要对调用模型model(x)进行预测,不要调用`model.forward(x))！否则，模型的hooks将无法工作。

# Sets learning rate - this is "eta" ~ the "n"-like
# Greek letter
lr = 0.1

# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
# Now we can create a model and send it at once to the device
model = ManualLinearRegression().to(device)

# Defines a SGD optimizer to update the parameters 
# (now retrieved directly from the model)
optimizer = optim.SGD(model.parameters(), lr=lr)

# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')

# Defines number of epochs
n_epochs = 1000

for epoch in range(n_epochs):
    model.train() # What is this?!?

    # Step 1 - Computes model's predicted output - forward pass
    # No more manual prediction!
    yhat = model(x_train_tensor)
    
    # Step 2 - Computes the loss
    loss = loss_fn(yhat, y_train_tensor)

    # Step 3 - Computes gradients for both "b" and "w" parameters
    loss.backward()
    
    # Step 4 - Updates parameters using gradients and the learning rate
    optimizer.step()
    optimizer.zero_grad()
    
# We can also inspect its parameters using its state_dict
print(model.state_dict())

输出：
OrderedDict([('b', tensor([1.0235])), ('w', tensor([1.9690]))])

2.1.6 训练 train

进入for循环的第一步就是执行model.train(),在PyTorch中，模型有model.train()方法，但该方法并没有真正执行训练步骤。它唯一的目的是将模型设置为训练模式。因为一些模型中可能会使用像Dropout这样的机制，它们在训练和评估阶段有不同的行为。

2.2 嵌套模型 Nested Models

linear = nn.Linear(1, 1)
linear

输出：
Linear(in_features=1, out_features=1, bias=True)

linear.state_dict()

输出：
OrderedDict([('weight', tensor([[-0.2191]])), ('bias', tensor([0.2018]))])

2.2.1 定义 model class

现在，使用PyTorch的线性模型作为自己的属性，从而创建一个嵌套的模型。__init__(self)中并不受限于定义参数，也可以包含其他模型作为其属性，所以很容易实现嵌套模型。

• 在__init__()函数中，创建了一个包含我们嵌套的线性模型这一属性。

• 在forward(self, x)函数中，调用嵌套模型本身来执行正向传递（注意，没有调用self.linear.forward(x)！）。

class MyLinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        # Instead of our custom parameters, we use a Linear model
        # with single input and single output
        self.linear = nn.Linear(1, 1)
                
    def forward(self, x):
        # Now it only takes a call
        self.linear(x)

2.2.2 查看参数

此时调用这个模型的parameters()方法，PyTorch将递归地计算出其属性的参数。另外，state_dict()同样可用。

torch.manual_seed(42)
dummy = MyLinearRegression().to(device)
list(dummy.parameters())

输出：
[Parameter containing:
 tensor([[0.7645]], requires_grad=True), Parameter containing:
 tensor([0.8300], requires_grad=True)]

dummy.state_dict()

输出：
OrderedDict([('linear.weight', tensor([[0.7645]])),
             ('linear.bias', tensor([0.8300]))])

2.3 序贯模型 Sequential Models

torch.manual_seed(42)
# Alternatively, you can use a Sequential model
model = nn.Sequential(nn.Linear(1, 1)).to(device)

model.state_dict()

输出：
OrderedDict([('0.weight', tensor([[0.7645]])), ('0.bias', tensor([0.8300]))])

2.4 层 Layers

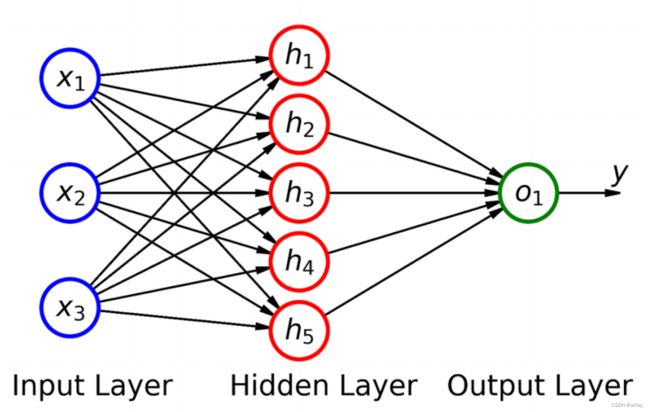
线性模型可以看作是神经网络中的一个层。

torch.manual_seed(42)
# Building the model from the figure above
model = nn.Sequential(nn.Linear(3, 5), nn.Linear(5, 1)).to(device)

model.state_dict()

输出：
OrderedDict([('0.weight', tensor([[ 0.4414,  0.4792, -0.1353],
                      [ 0.5304, -0.1265,  0.1165],
                      [-0.2811,  0.3391,  0.5090],
                      [-0.4236,  0.5018,  0.1081],
                      [ 0.4266,  0.0782,  0.2784]])),
             ('0.bias', tensor([-0.0815,  0.4451,  0.0853, -0.2695,  0.1472])),
             ('1.weight',
              tensor([[-0.2060, -0.0524, -0.1816,  0.2967, -0.3530]])),
             ('1.bias', tensor([-0.2062]))])

由于这个序贯模型没有属性名称，所以state_dict()使用了数字前缀。

我们可以使用模型的add_module()方法来命名图层：

torch.manual_seed(42)
# Building the model from the figure above
model = nn.Sequential()
model.add_module('layer1', nn.Linear(3, 5))
model.add_module('layer2', nn.Linear(5, 1))
model.to(device)

输出：
Sequential(
  (layer1): Linear(in_features=3, out_features=5, bias=True)
  (layer2): Linear(in_features=5, out_features=1, bias=True)
)

目前我们只使用了一个Linear Layers。在PyTorch中有许多不同的图层可供使用：

• Convolution Layers
• Pooling Layers
• Padding Layers
• Non-linear Activations
• Normalization Layers
• Recurrent Layers
• Transformer Layers
• Linear Layers
• Dropout Layers
• Sparse Layers (embeddings)
• Vision Layers
• DataParallel Layers (multi-GPU)
• Flatten Layer

2.5 code整合

到目前为止，我们已经学习了很多基本术语和相关操作，从在Numpy中使用梯度下降训练线性回归，到逐步将其转换为PyTorch模型。现在把它们全部放在一起，并把我们的代码重构成三个基本部分，即：

2.5.1 准备数据

%%writefile data_preparation16.py

device = 'cuda' if torch.cuda.is_available() else 'cpu'

# Our data was in Numpy arrays, but we need to transform them
# into PyTorch's Tensors and then we send them to the 
# chosen device
x_train_tensor = torch.as_tensor(x_train).float().to(device)
y_train_tensor = torch.as_tensor(y_train).float().to(device)

输出：
Overwriting data_preparation16.py

%run -i data_preparation16.py

2.5.2 设置模型

%%writefile model_configuration16.py

# This is redundant now, but it won't be when we introduce
# Datasets...
device = 'cuda' if torch.cuda.is_available() else 'cpu'

# Sets learning rate - this is "eta" ~ the "n"-like Greek letter
lr = 0.1

torch.manual_seed(42)
# Now we can create a model and send it at once to the device
model = nn.Sequential(nn.Linear(1, 1)).to(device)

# Defines a SGD optimizer to update the parameters 
# (now retrieved directly from the model)
optimizer = optim.SGD(model.parameters(), lr=lr)

# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')

输出：
Overwriting model_configuration16.py

%run -i model_configuration16.py

2.5.3 训练模型

%%writefile model_training16.py

# Defines number of epochs
n_epochs = 1000

for epoch in range(n_epochs):
    # Sets model to TRAIN mode
    model.train()

    # Step 1 - Computes model's predicted output - forward pass
    yhat = model(x_train_tensor)
    
    # Step 2 - Computes the loss
    loss = loss_fn(yhat, y_train_tensor)

    # Step 3 - Computes gradients for both "b" and "w" parameters
    loss.backward()
    
    # Step 4 - Updates parameters using gradients and  the learning rate
    optimizer.step()
    optimizer.zero_grad()

输出：
Overwriting model_training16.py

%run -i model_training/v0.py

print(model.state_dict())

输出：
OrderedDict([('0.weight', tensor([[1.9690]])), ('0.bias', tensor([1.0235]))])

3. 知识点小结

• 1.使用梯度下降实现线性回归
• 2.在PyTorch创建张量，发送到device，并利用它们生成参数
• 3.理解PyTorch的主要特性，如autograd, backward(),grad, zero_(), and no_grad()
• 4.可视化动态计算图与一系列相关的操作
• 5.创建一个优化器同时使用step() and zero_grad()更新多个参数
• 6.使用PyTorch相应的高阶函数创建损失函数loss function
• 7.理解PyTorch的模块类并创建自己的模型，实现 __init__() and forward()方法，并利用其 parameters() and state_dict()方法
• 8.使用上面的函数将原始的Numpy实现转换为PyTorch实现
• 9.了解在模型迭代过程中包含 model.train()重要性
• 10.使用PyTorch的层实现嵌套模型和序贯模型
• 11.核心代码的整合，分为三个模块：数据准备、模型构建、模型训练