C语言基础题练习10道

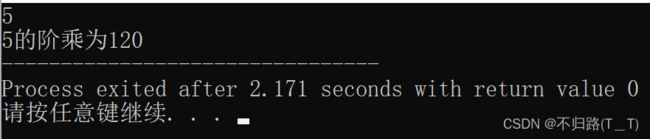
1、题目：求n的阶乘

#include
int main()
{
	int n,result;
	scanf("%d",&n);
	if(n>=1){
		result=1; 
		for(int i=2;i<=n;i++){
			result*=i; 
		}
		printf("%d的阶乘为%d",n,result); 
	} 
	else{
		printf("请输入大于1的正整数"); 
	}
	return 0;
}

2、计算 1+1/2+1/3+…1/20=?

#include
int main()
{
	double result=0.0;
	for(int i=1;i<=20;i++){
		result+=1.0/i;
	}
	printf("1+1/2+1/3+...+1/20=%f",result);
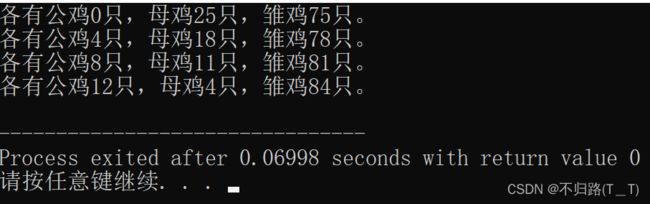
	return 0;
}

3、百钱买百鸡

5 文钱可以买一只公鸡，3 文钱可以买一只母鸡，1 文钱可以买 3 只雏鸡。现在用 100 文钱买 100 只鸡，那么各有公鸡、母鸡、雏鸡多少只？
思路：典型数学题，可以先用数学方法得到式子，再求解。

#include
int main()
{
	int x,y,z;
	for(int i=0;i<=20;i++){
		for(int j=0;j<=33;j++){
			z=100-i-j;
			if(z%3==0&&5*i+3*j+z/3==100){
				printf("各有公鸡%d只，母鸡%d只，雏鸡%d只。\n",i,j,z);
			}
		}
	}
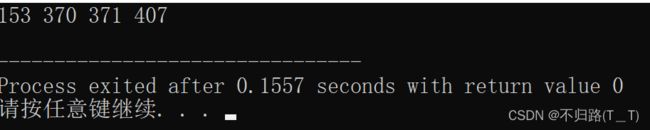
	return 0;
}

4、水仙花数

如果一个 3 位数等于其各位数字的立方和，则称这个数为水仙花数。
例如：153 = 1^3 + 5^3 + 3^3，因此 153 就是一个水仙花数
编写程序打印出所有的水仙花数

#include
int main()
{
	int x,y,z;
	for(int i=100;i<=999;i++){
		x=i/100;//得到百位的数字
		y=(i-100*x)/10;//得到十位的数字；
		z=i%10;//得到个位的数字
		if(x*x*x+y*y*y+z*z*z==i){
			printf("%d ",i);
		} 
	}
	printf("\n");
	return 0;
}

5、分解质因数

将一个整数分解质因数。例如：输入 90,打印出 90=233*5
没做出来

#include
void main()
{
	int i, n;
	printf("输入需要分解的整数：");
	scanf("%d", &n);
	for (i = 2; i <= n; i++) {
		while (n%i==0){
			printf("%d", i);
			n /= i;
			if (n != 1)printf("*");
		}
	}
}

6、exchange 两数交换

编写一个函数 exchange(a,b), 函数功能是交换 a，b 两个参数的值

#include
void exchange(int &a,int &b){
	int t;
	t=a;a=b;b=t;
}
int main()
{
	int a,b;
	scanf("%d %d",&a,&b);
	exchange(a,b);
	printf("%d %d",a,b);
	return 0;
}

7、斐波那契数列

斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13,特别指出：第 0 项是 0，第 1 项是第一个 1。从第三项开始，每一项都等于前两项之和。
用户输入一个正整数 n 后系统输出前 n 项斐波那契数列。
思路:反向思路，输出第a项时，保存第a+1、a+2项的值。其中a+2的值会等于第a项+第a+1项。2个变量来记录保存每次的后两项，不断更新这两个变量的值。

#include
int main()
{
	int x,t1=0,t2=1,next;
	scanf("%d",&x);
	for(int i=1;i<=x;i++){
		printf("%d,",t1);
		next=t1+t2;
		t1=t2;
		t2=next;
	}
	printf("\n");
	return 0;
}

递归法：

#include
int fei(int n){
	if(n==1){
		return 0;
	}
	if(n==2){
		return 1;
	}
	fei(n)=fei(n-1)+fei(n-2);
}
int main()
{
	int x;
	scanf("%d",&x);
	for(int i=1;i<=x;i++){
		printf("%d,",fei(i));
	}
	printf("\n");
	return 0;
}

8、开关灯问题

有 n 盏灯，编号为 0~n。
第一个人把所有灯打开；第二个人按下所有编号为 2 的倍数的开关（这些灯将关掉）；第三个人按下所有编号是 3 的倍数的开关（其中关掉的灯将被打开，开着的灯将被关掉）；依次类推，一共有 k 个人，问最后有哪些灯开着，输入 n 和 k，输出开着的灯的编号。k<=n<=1000。
思路：可以用数组表示每盏灯的状态。-1为关闭，1为开。依次遍历，每次被按就乘以-1.

#include
int main()
{
	int a[1000],n,k;
	scanf("%d %d",&n,&k);
	//n盏灯初始状态是关闭 
	for(int i=1;i<=n;i++){
		a[i]=0;
	}
	//k个人 
	for(int j=1;j<=k;j++){
		//第j个人按编号为j的倍数的灯 
		for(int l=j;l<=n;l++){
			if(l%j==0){
				a[l]*=-1;
			}
		}
	}
	//值为1的下标就是开着的灯编号 
	for(int i=1;i<=n;i++){
		if(a[i]==1){
			printf("%d,",i);
		} 
	}
	return 0;
}

9、找赛手

2 个羽毛球队比赛，各出 3 人，每个人只比一次，甲队为 A、B、C 三人，乙队为 X、Y、Z 三人，有人打听比赛名单，A 说他不和 X 比，C 说不和
X、Z 比，请用编程打印出三队赛手比赛名单
没做出来
参考链接https://blog.csdn.net/weixin_51609435/article/details/120613055
思路：遍历。确保不重复比赛的情况下，满足A 说他不和 X 比，C 说不和X、Z 比

#include
int main()
{
	int a, b, c;  //a是A的对手 b是B的对手 c是C的对手
		for (a = 'X'; a <= 'Z'; a++)
		{
			for (b = 'X'; b <= 'Z'; b++)
			{
				if (a != b)//避免重复比赛
				{
					for (c = 'X'; c <= 'Z'; c++)
				    {
						if (a != c&&b!=c)//避免重复比赛
						{
							if (a != 'X' && c != 'X' && c != 'Z')
							{
								printf(" A对%c\n B对%c\n C对%c", a, b, c);
							}
						}
					}
				}
			}	
		}	
	return 0;
}

10、谁在作案

某处发生一起案件，侦查得到以下线索
ABCD 四人都有作案可能
AB 中至少有一人参与作案
BC 中至少有一人参与作案
CD 中至少有一人参与作案
AC 中至少有一人未参与作案
请用编程的方式得出，谁最有可能作案

#include
#include
int main()
{
	int a, b, c,d;  //a是A的对手 b是B的对手 c是C的对手
	int t[4]={0,0,0,0};//记录每种可能中它们犯罪的总次数 
	for(a=0;a<=1;a++){
		for(b=0;b<=1;b++){
			for(c=0;c<=1;c++){
				for(d=0;d<=1;d++){
					if((a==1||b==1)&&(b==1||c==1)&&(c==1||d==1)&&(a==0||c==0)){
						t[0]+=a;t[1]+=b;t[2]+=c;t[3]+=d;
					}
				}
			} 
		}
	}
	int max=0;
	char ch[4]={'A','B','C','D'};
	//得到犯罪可能性次数最多的数字 
	for(int i=1;i<4;i++){
		if(t[i]>max){
			max=t[i];
		}
	}
	//可能有多个人可能性相同，此时，次数为最多的都是最可能的 
	for(int j=0;j<4;j++){
		if(t[j]==max){
			printf("%c最有可能作案。",ch[j]);
		}
	}	
	return 0;
}