MATLAB 之 其他形式的二维图形

• 二维图线除采用直角坐标系外，还可采用对数坐标或极坐标。除了绘制二维曲线外，MATLAB 的二维图形还包括各种二维统计分析图形。

一、对函数自适应采样的绘图函数

• 在上一篇博客当中，我们介绍了 plot 函数。
• 其基本的操作方法为，先取足够稠密的自变量向量 $x$，然后计算出函数值向量 $y$，最后用绘图函数绘图。在取数据点时一般都是等间隔采样，这对绘制高频率变化的函数不够精确。例如函数 $f(x)=cos(tan(\pi x))$，在 (0, 1) 范围有无限多个振荡周期，函数变化率大。
• 为提高精度，绘制出比较真实的函数曲线，就不能等间隔采样，而必须在变化率大的区段密集采样，以充分反映函数的实际变化规律，进而提高图形的真实度。
• fplot 函数可自适应地对函数进行采样，能更好地反映函数的变化规律，其调用格式如下：

    fplot(filename,lims,选项) 

• 其中，filename 代表一个函数，通常采用函数句柄的形式，也可以是字符串形式，很多 MATLAB 函数都有这种用法。可以指定多个分量函数，这时要以单元向量表示。lims 为 x 轴的取值范围，取二元向量 [xmin, xmax]，默认值为 [ -5,5]。选项定义与 plot 函数相同，例如：

f=@sin;  %利用函数句柄指定函数
fplot(f, [0,2*pi],'*')  %绘制正弦曲线
fplot('sin(1./x)',[0.01,0.1])  %利用字符串指定函数，但以后的版本将不支持
fplot({@(x)sin(x),@(x)cos(x)},[0,2*pi],'r.')  %利用匿名函数指定函数

• 观察上述语句绘制的正、余弦曲线采样点的分布，可以发现曲线变化率大的区段，采样点比较密集。
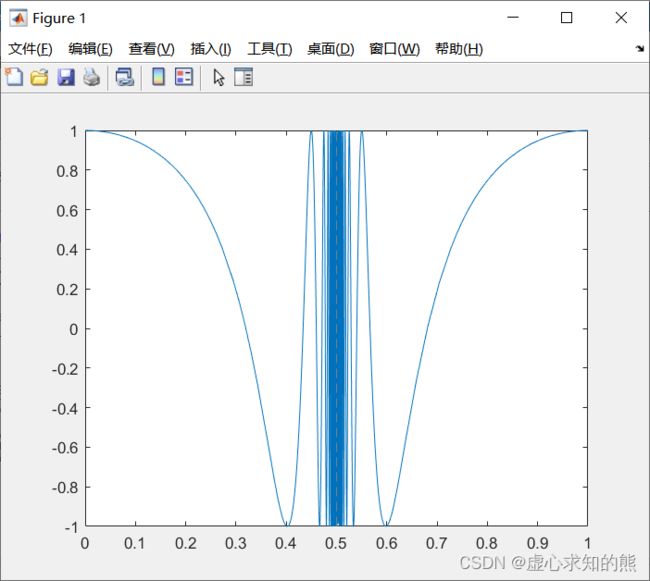
• 例如，我们用 fplot 函数绘制 $f(x)=cos(tan(\pi x))$ 的曲线。
• 命令如下：

fplot(@(x)cos(tan(pi*x)),[0,1])

• 程序运行结果如下图所示。

二、其他坐标系下的二维曲线图

1. 对数坐标函数

• 在工程应用中，经常用到对数坐标，例如自动控制理论中的 Bode 图就采用对数坐标。MATLAB 提供了绘制半对数和全对数坐标曲线的函数，调用格式如下：

    semilogx(x1,y1,选项1,x2,y2,选项2,…)
    semilogy(xl,y1,选项1,x2,y2,选项2,…)
    loglog(xl,y1,选项1,x2,y2,选项2,…)

• 其中，选项的定义与 plot 函数完全一致，所不同的是坐标轴的选取。
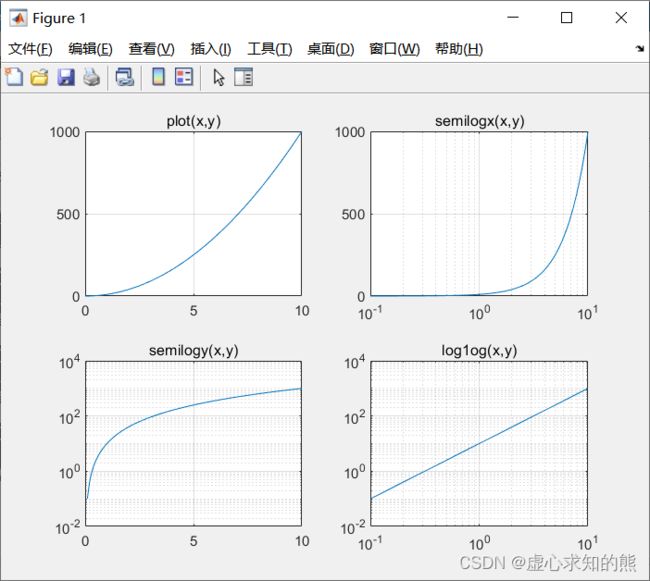
• semilogx 函数使用半对数坐标，$x$ 轴为常用对数刻度，而 $y$ 轴仍保持线性刻度。
• semilogy 函数也使用半对数坐标，$y$ 轴为常用对数刻度，而 $x$ 轴仍保持线性刻度。
• loglog 函数使用全对数坐标，$x$ 轴和 $y$ 轴均采用常用对数刻度。
• 例如，我们绘制 $y=10x^2$ 的对数坐标图并与直角线性坐标图进行比较。
• 程序如下：

x=0:0.1:10;
y=10*x.*x;

subplot(2,2,1);
plot(x,y);  %直角坐标曲线
title('plot(x,y)');
grid on;

subplot(2,2,2);
semilogx(x,y);  %x半对数坐标曲线
title('semilogx(x,y)');
grid on;  

subplot(2,2,3);
semilogy(x,y);  %y半对数坐标曲线
title('semilogy(x,y)');
grid on;

subplot(2,2,4);
loglog(x,y);  %全对数坐标曲线
title('log1og(x,y)');
grid on;

• 程序运行结果如下。

2. 极坐标图

• polar 函数用米绘制极坐标图，其调用格式如卜：

    polar(theta,rho,选项)

• 其中，theta 为极坐标极角，rho为极坐标极径，选项的内容与 plot 函数相似。
• 例如，蝴蝶曲线是一种富有美感的平面曲线，其极坐标方程如下：$$\rho =e^{\cos \theta }-2\cos 4\theta +{\sin }^5\frac{\theta }{12}$$
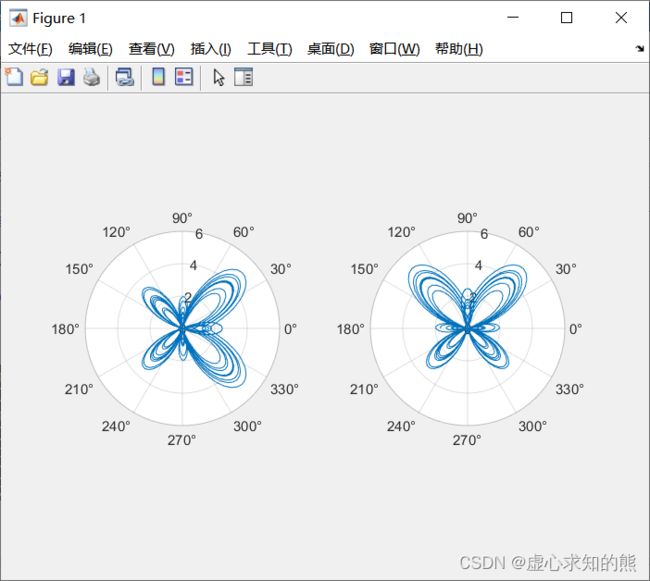
• （1） 绘制蝴蝶曲线。
• （2） 调整 $\theta$ 的大小可以改变曲线形状及其方向，将 $\theta$ 减 $\frac{\pi }{2}$，使图形旋转90°，绘制蝴蝶曲线。
• 程序如下：

t=0:pi/50:20*pi;
r1=exp(cos(t))-2*cos(4*t)+sin(t/12).^5;
r2=exp(cos(t-pi/2))-2*cos(4*(t-pi/2))+sin((t-pi/2)/12).^5;
subplot(1,2,1)
polarplot(t,r1)  %绘制蝴蝶曲线
subplot(1,2,2)
polarplot(t,r2)  %旋转90°的蝴蝶曲线

• 程序运行结果如下图所示。

三、其他特殊二维图像

• 除二维曲线外，MATLAB 还可以绘制其他特殊二维图形，包括用于统计分析的条形图、直方图、饼图、散点图等。

1. 条形类图形

• 条形类图形用一系列高度不等的条纹表示数据大小，常用的有条形图和直方图。条形图用于显示不同时间点的数据大小或比较各组数据之间的大小，直方图用于表示数据分布的情况。
• （1） 条形图。绘制二维条形图的函数为 bar（垂直条形图）与 barh（水平条形图），它们的调用格式是一样的。以 bar 函数为例，常用的调用格式如下：
• ① bar(y)：若 y 为向量，则分别显示每个分量的高度，横坐标为 y 的下标。若 y 为矩阵，则分别比较 y 的每一行元素的大小， 横坐标为矩阵的行数。
• ② bar(x,y,style)：在指定的横坐标 x 画出 y。当 y 是 $m\times n$ 矩阵时，矩阵中每一行元素绘制在一组中，每一列元素绘制在每组中相对应的 x 位置上。style 指定条形的排列模式，类型有 grouped（簇状分组）和 stacked（堆积分组），默认采用 grouped 排列模式。
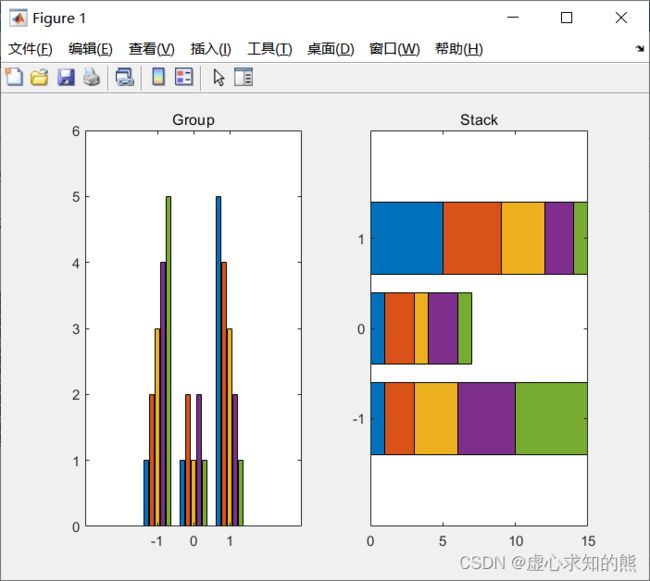
• 条形图应用实例。
• 程序如下：

x=-1:1;
y=[1,2,3,4,5;1,2,1,2,1;5,4,3,2,1];
subplot(1,2,1);
bar(x,y,'grouped');
title('Group');
axis([-3,3,0,6]);
subplot(1,2,2);
barh(x,y,'stacked');
title('Stack');

• 程序运行结果如下图所示。

• （2） 直方图。在 MATLAB 中，绘制直方图的函数有两个：hist 函数和 rose 函数，分别用于绘制直角坐标系下的直方图和极坐标系下的直方图，后者也称为玫瑰花图。
• hist 函数的应用更为广泛一些，其调用格式如下：

    hist(y[,x])

• 如果 y 为向量，则将 y 中的最小值和最大值之间的数值区间等分，并统计每个区间中向量元素的个数，然后以元素个数为高度绘制条形图。
• 如果 y 为矩阵，hist 函数将 x 的每一列作为一个向量，绘制每一列元素的直方图。
• 选项 x 用于设置统计区间的划分方式，若 x 是标量，则统计区间均分成 x 个小区间；若 x 是向量，则区间数为向量的长度，向量中的每一个数指定各区间的中心点，省略 x 时，按 10 个等分区间统计。
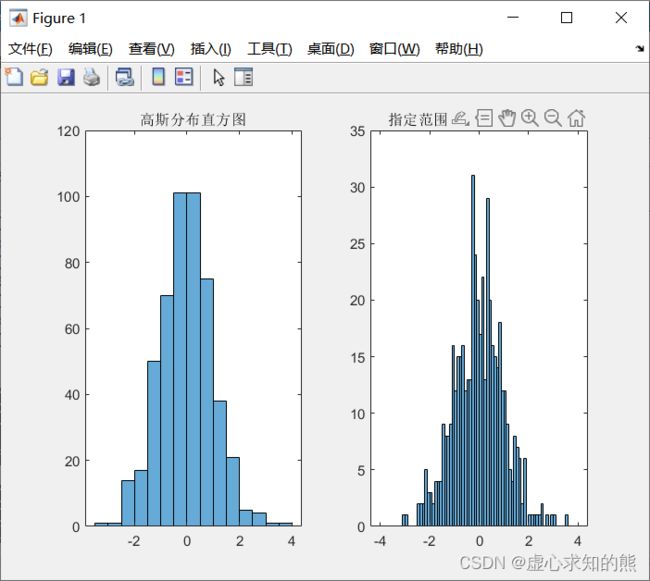
• 例如，我们绘制服从高斯分布的直方图，再将这些数据分到指定范围的区间中，并绘制在直方图中。
• 程序如下：

y=randn(500,1);
subplot(1,2,1);
histogram(y);
title('高斯分布直方图');
x=-4:0.1:4;
subplot(1,2,2);
histogram(y,x);
title('指定范围的高斯分布直方图');

• 程序运行结果如下图所示。

• rose 函数的调用格式与 hist 函数非常相似，调用方法如下：

    rose (theta[,x])

• 其中，向量 theta 用于确定每一区间与原点的角度（角度以弧度为单位），每一区间长度反映出落入该区间的 theta 元素的个数。
• 若 x 是标量，则在 [0, 2n] 区间内画出 x 个等距的小扇形，默认值为 20。若 x 是向量，则 x 指定分组中心值，x 中元素的个数为数据分组数。
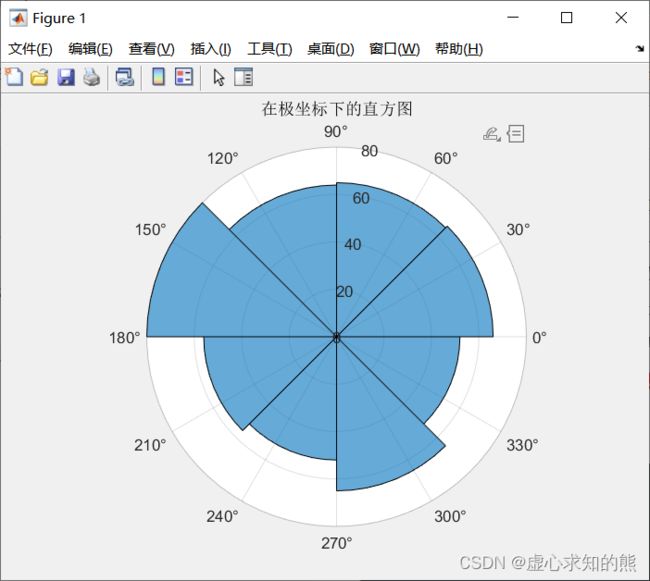
• 例如，我们绘制上例高斯分布数据在极坐标下的直方图。
• 程序如下：

y=randn(500,1);
theta=y*pi;
polarhistogram(theta);
title('在极坐标下的直方图');

• 程序运行结果如下图所示。

2. 面积类图形

• （1） 扇形统计图。扇形统计图又称为饼图，反映一个数据系列中各个分量在总数量中所占的比重。MATLAB 提供了 pie 函数来绘制扇形统计图，其调用格式如下：

    pie(x,explode)

• pie 函数使用 x 中的数据绘制饼图，x 可以是向量或矩阵。如果 x 为向量，则 x 的每个元素占有一个扇形，从饼图的正上方开始，按逆时针顺序分别为 x 的各个元素。如果 x 为矩阵，则按照列的顺序依次排列矩阵元素。
• 如果 x 的全部元素之和小于 1，则绘制的图形不是完整的圆。explode 是与 x 同等大小的向量或矩阵，与 explode 的非零值对应的部分将从饼图中心分离出来。当我们省略 explode 时，饼图是一个整体。
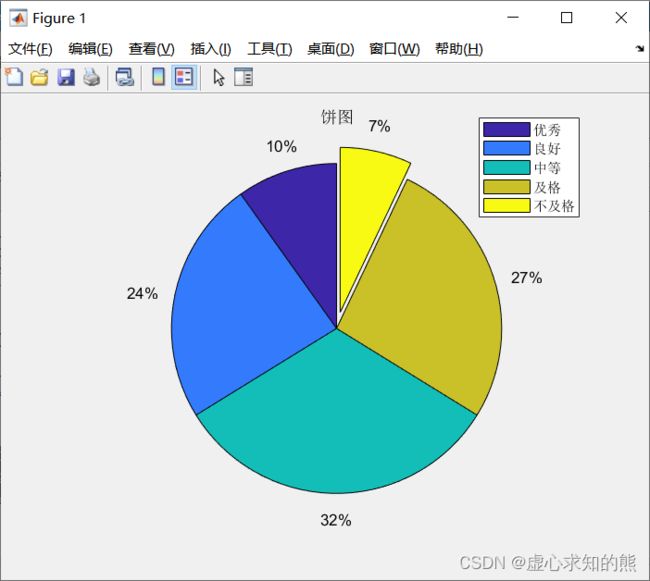
• 例如，某次考试优秀、良好、中等、及格、不及格的人数分别为 7、17、23、19、5，我们试用扇形统计图作成绩统计分析。
• 程序如下：

pie([7,17,23,19,5],[0,0,0,0,1]);  %对应第5分量部分从饼图中心分离
title('饼图');
legend('优秀','良好','中等','及格','不及格');

• 程序运行结果如下图所示。

• （2） 面积统计图。面积统计图反映数量变化的趋势，在实际中可以表现不同部分对整体的影响。在 MATLAB 中，绘制面积统计图的函数是 area，其调用格式如下。
• ① area(x)：与 plot(x) 函数一样， 但是将所得曲线下方的区域填充颜色。
• ② area(x,y)：如果 x、y 均为向量，与 plot(x,y) 一样，但将所得曲线下方的区域填充颜色。如果 x 为向量，y 为矩阵，则矩阵 y 的第一列对向量 x 绘图，然后依次是下一列与前面所有列值的和对向量 x 绘图，每个区域有各自的颜色。
• 例如，我们绘制一个面积统计图。
• 程序如下：

x=1:2:9;
y=[1,3,5,2,6;2,4,5,6,2;5,4,7,2,2]';
area(x,y);
grid on;
title('面积统计图');

• 程序运行结果如下图所示。

• 在此，我们对这幅图进行简要分析。
• 首先，x 的元素是 [1，3，5，7，9] 的向量，而 y 是三行五列矩阵的转置，因此，y 就是五行三列。
• 然后，向量 x 分别对应 y 的三列，也就是当 x 为 1 时，y 的取值分别是 1，2，5；当 x 为 3 时，y 的取值分别是 3，4，4；当 x 为 5 时，y 的取值分别是 5，5，7；当 x 为 7 时，y 的取值分别是 2，6，2；当 x 为 10 时，y 的取值分别是 6，2，2。
• 这里需要注意的是，他们需要依次累加。
• （3） 实心图。实心图是将数据的起点和终点连成多边形，并填充颜色。绘制实心图的函数是 fill，其调用格式如下：

    fill(x,y,颜色)

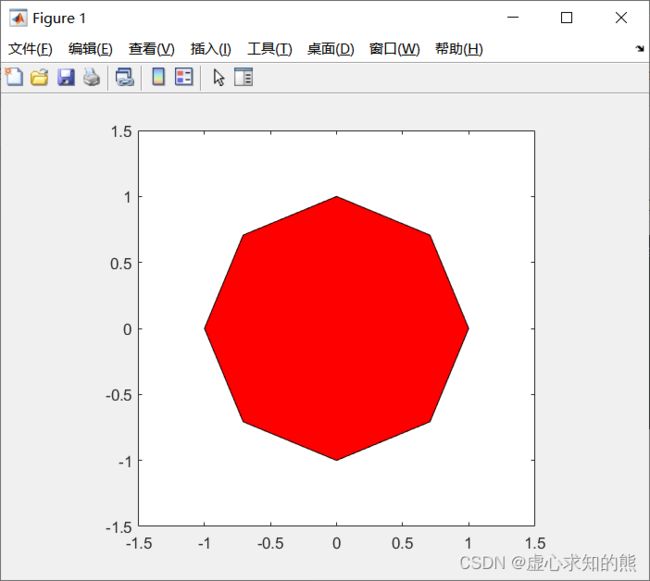
• fill 函数按向量元素下标渐增次序依次用直线段连接 x、y 对应元素定义的数据点。假若这样连接所得折线不封闭，那么 MATLAB 将自动把该折线的首尾连接起来，构成封闭多边形，然后将多边形内部涂满指定的颜色。
• 例如，我们绘制一个红色的正八边形。
• 程序如下：

t=0:2*pi/8:2*pi;  %取正八边形坐标点
t=[t,t(1)];  %数据向量的首尾重合，使图形封闭
x=sin(t);
y=cos(t);
fill(x,y,'r');  %x、y是圆周坐标，数据间隔足够小时可以画圆
axis equal;
axis([-1.5,1.5,-1.5,1.5]);

• 程序运行结果如下图所示。

3. 散点类图形

• 散点类图形经常用于实验中，比较实验得到的结果与理论值之间的差异，并根据实验误差的特征曲线研究误差的规律，得出实验中研究的对象主体与对象主体相关事物之间的关系。
• MATLAB 提供了绘制散点类图形的函数 scatter、stairs 和 stem，分别用于绘制散点图、阶梯图和杆图。3 个函数的调用格式如下：

    scatter(x,y[,'filled'][,颜色])
    stairs(x,y,选项)
    stem(x,y,选项)

• 3 个函数的用法与 plot 函数相似。一-般情况下，x、y 为同等大小的向量，用于定位数据点。scatter 函数的 filled 选项表示填充绘图点，省略时，数据点是空心的。
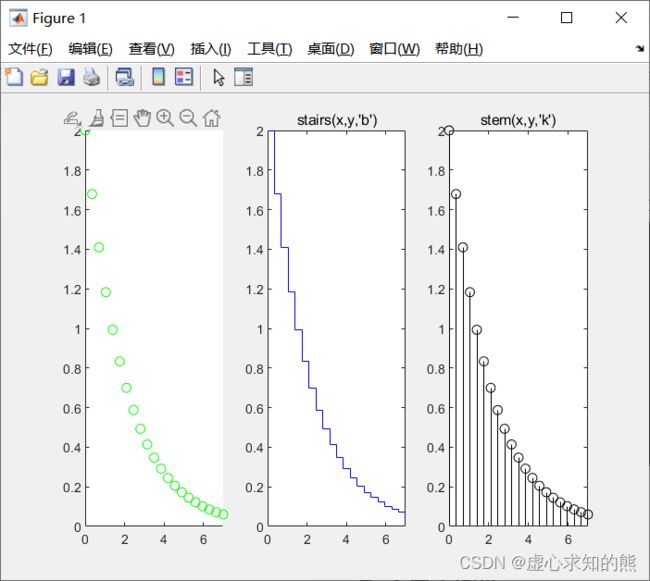
• 例如，我们分别以散点图、 阶梯图和杆图形式绘制曲线 $y=2e^{-0.5x}$。
• 程序如下：

x=0:0.35:7;
y=2*exp(-0.5*x);
subplot(1,3,1);
scatter(x,y,'green');
title('scatter(x,y,''g'')');
axis([0,7,0,2]);
subplot(1,3,2);
stairs(x,y,'b');
title('stairs(x,y,''b'')');
axis([0,7,0,2]);
subplot(1,3,3);
stem(x,y,'k');
title('stem(x,y,''k'')');
axis([0,7,0,2]);

• 程序运行结果如下图所示。

4. 矢量类图形

• 矢量由两个参数指定，分别代表矢量的 x 分量和 y 分量，也可以由一个复数指定，复数的实部和虚部分别代表矢量的 x 分量和 y 分量。矢量类图形有罗盘图、羽毛图和箭头图，MATLAB 提供了绘制这些图形的函数。
• （1） 罗盘图。罗盘图表示起点为坐标原点的向量，同时还在坐标系中显示圆形的分隔线。绘制这种图形的函数是 compass，其调用格式如下。
• ① compas(x,y)：x、 y 为 n 个元素的向量，函数显示 n 个箭头，箭头的起点为原点，箭头的位置为 (x(i)),y(i))。
• ② compass(z)：z 为 n 个元素的复数向量，函数显示 n 个箭头，箭头的起点为原点，箭头的位置为 (real(z),imag(z))。real(z) 和 imag(z) 分别代表复数向量的实部和虚部。
• （2） 羽毛图。羽毛图是在横坐标上等距地显示向量的图形，看起来就像鸟的羽毛一样。绘制羽毛图的函数是 feather，其调用格式如下。
• ① feather(x,y)：绘制由 x 与 y 确定的向量。
• ② feather(z)：绘制由 z 确定的向量，等价于 feather(real(z),imag(z))。
• （3） 箭头图。上面两个函数绘制的图形也可以叫箭头图，但这里的箭头图能更好地表示矢量，它的箭头方向代表矢量方向，箭头长短表示矢量的大小。绘制这种图形的函数是 quiver，其调用格式如下：

    quiver([x,y,]u,v)

• 其中，(x, y) 为矢量起点，(u, v) 为待绘制的矢量。x、y、u、v 必须是同型矩阵，若省略 x、y，则在平面上均匀取若千个点作为起点。
• 例如，我们分别以罗盘图、羽毛图和箭头图形式绘制正弦曲线。
• 程序如下：

x=-pi:pi/8:pi;
y=sin(x);
subplot(2,2,1);
compass(x,y);
title('罗盘图');
subplot(2,2,2);
feather(x,y);
title('羽毛图');
subplot(2,1,2);
quiver(x,y);
title('箭头图');

• 程序运行结果如下图所示。