动态规划II （42、53、64、70、72）

CP42 接雨水

题目描述：

学习记录：

虽然脑子里第一个蹦出双指针，但是题目是动态规划，两个混着想，啥也没想出来...不会

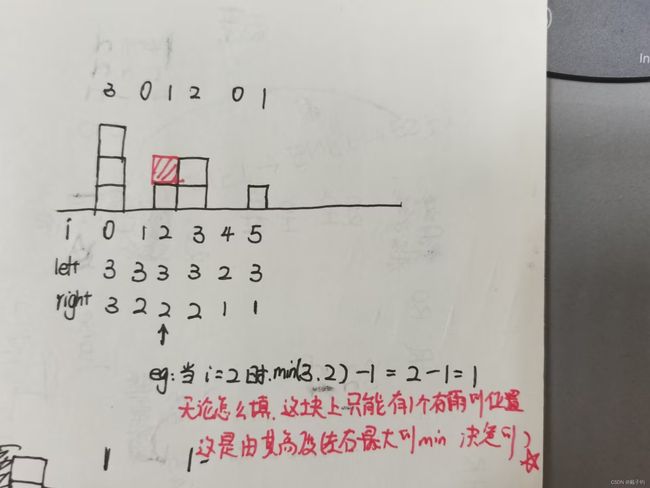
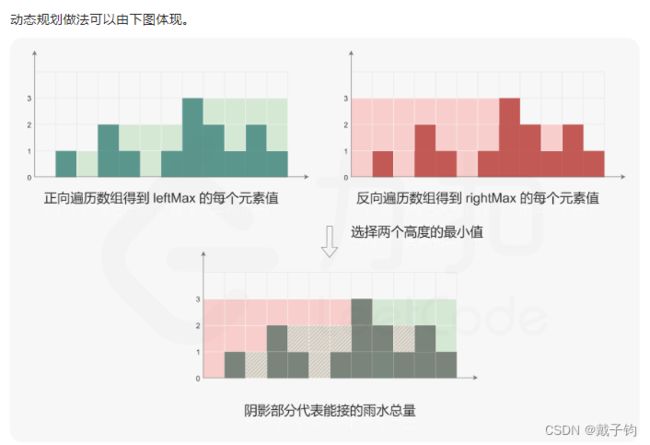
1.动态规划：太牛了吧，这个不是从整体去考虑每一块该怎么填，而是通过判断每一个位置上的雨水的量进行判断的

//题解
class Solution {
public:
    int trap(vector& height) {
        int n = height.size();
        if (n == 0) {
            return 0;
        }
        vector leftMax(n);
        leftMax[0] = height[0];
        for (int i = 1; i < n; ++i) {
            leftMax[i] = max(leftMax[i - 1], height[i]);
        }

        vector rightMax(n);
        rightMax[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; --i) {
            rightMax[i] = max(rightMax[i + 1], height[i]);
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans += min(leftMax[i], rightMax[i]) - height[i];
        }
        return ans;
    }
};

//后来按这个思路自己写
class Solution {
public:
    int trap(vector& height) {
        int n=height.size();
        int result=0;

        vector leftMax(n);
        leftMax[0]=height[0];
        for(int i=1;i rightMax(n);
        rightMax[n-1]=height[n-1];
        for(int j=n-2;j>=0;j--)
        {
            rightMax[j]=max(rightMax[j+1],height[j]);
        }

        for(int k=0;k

 2.双指针：和动态规划思想一样，就是省去了两个数组，并且也不需要两边的最大距离，只需要在这个地方能存储的最大即可

//题解
class Solution {
public:
    int trap(vector& height) {
        int ans = 0;
        int left = 0, right = height.size() - 1;
        int leftMax = 0, rightMax = 0;
        while (left < right) {
            leftMax = max(leftMax, height[left]);
            rightMax = max(rightMax, height[right]);
            if (height[left] < height[right]) {
                ans += leftMax - height[left];
                ++left;
            } else {
                ans += rightMax - height[right];
                --right;
            }
        }
        return ans;
    }
};

CP53 最大子数组

题目描述：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组 是数组中的一个连续部分。

学习记录：

一道很经典的动态规划，如果当前和为整数，就继续往后加，如果和为负数，就等于下一个数，并在过程中记录最大的和即可。应该是做过，这个想法很自然的出现在我脑子里。

class Solution {
public:
    int maxSubArray(vector& nums) {
        int now=nums[0];int result=nums[0];
        for(int i=1;i

经典解法是定义一个记录的数组，记录当前最大的和。但是由于数组之前的元素在后面都没有被用到了，只需要一个数记录就可了，省空间。

CP64 最小路径和

题目描述：

学习记录：

简单动态规划，判断即可

CP70 爬楼梯

题目描述：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

学习记录：

f(x)=f(x−1)+f(x−2)，初始化不搞错就行f(1)=1,f(2)=2

CP72 编辑距离

题目描述：

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。你可以对一个单词进行如下三种操作：插入一个字符；删除一个字符；替换一个字符

学习记录：

做过，有记忆定义word1长度为i，word2长度为j，定义数组tmp[i][j]代表从word1前i个到word2前j个所需要的最少操作数。有点肝不动了，上题解

 注意这里多加了一行一列

//题解
class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.length();
        int m = word2.length();

        // 有一个字符串为空串
        if (n * m == 0) return n + m;

        // DP 数组
        vector> D(n + 1, vector(m + 1));

        // 边界状态初始化
        for (int i = 0; i < n + 1; i++) {
            D[i][0] = i;
        }
        for (int j = 0; j < m + 1; j++) {
            D[0][j] = j;
        }

        // 计算所有 DP 值
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < m + 1; j++) {
                int left = D[i - 1][j] + 1;
                int down = D[i][j - 1] + 1;
                int left_down = D[i - 1][j - 1];
                if (word1[i - 1] != word2[j - 1]) left_down += 1;
                D[i][j] = min(left, min(down, left_down));

            }
        }
        return D[n][m];
    }
};