排序算法总结
常见排序算法的时间复杂度、空间复杂度及稳定性分析:
| 时间复杂度 | 空间复杂度 | 是否有稳定性 | ||
| 基于比较的排序算法 | 选择排序 | O(N^2) | O(1) | 否 |
| 冒泡排序 | O(N^2) | O(1) | 是 | |
| 插入排序 | O(N^2) | O(1) | 是 | |
| 归并排序 | O(N*logN) | O(N),每次需要额外一个数组用于拷贝 | 是 | |
| 快排 | O(N*logN) | O(logN) | 否 | |
| 堆排序 | O(N*logN) | O(1),数组本身可以作为堆,用的只是有限几个变量 |
否,堆插入的过程不稳定如果最后插入一个 | |
| 不基于比较的排序算法 | 计数排序 | O(N) | O(M),M表示数的枚举值个数 | 是 |
| 基数排序 | O(N) | O(N) | 是 |
(1)不基于比较的排序,对样本数据有严格的要求,不易改写
(2)基于比较的排序,只要规定好两个样本怎么比大小就可以直接复用。
(3)基于比较的排序,时间复杂度的极限是O(N*logN)
(4)时间复杂度为O(N*logN),额外空间复杂度低于O(N)且稳定的基于比较的排序是不存在的。
(5)为了绝对速度选快排,为了省空间选堆排,为了稳定性选归并
稳定性分析:
选择排序:肯定做不到稳定性,比如原来的数组是[5,5,5,5,5,3,5,5],每次选最小的与0位置做交换,那原来0位置的5会越过1,2,3,4位置的5来到5位置。
冒泡排序:取决于相等的时候怎么处理相等,如果相等不交换就能保证稳定(如果相等还要交换的话也就不会有稳定性了)
插入排序:和冒泡排序一样,取决于怎么处理相等。
归并排序:也是处理相等的时候,相等的时候先拷贝左边的就可以保证稳定性(先拷贝右边不行,因为左组的元素在原来数组中是在右组的元素之前的)。
快速排序:无法保证稳定性,因为Partition过程做不到稳定,比如原数组是[4,4,4,4,1,4,3],我们以快排1.0为例,先选数组最后一个数字去做划分值,当遍历到4为止的1的时候,1比3小,需要和0位置的4做交换,0位置的4换到了4位置,跨过了1,2,3位置的4,其他快排也是类似的
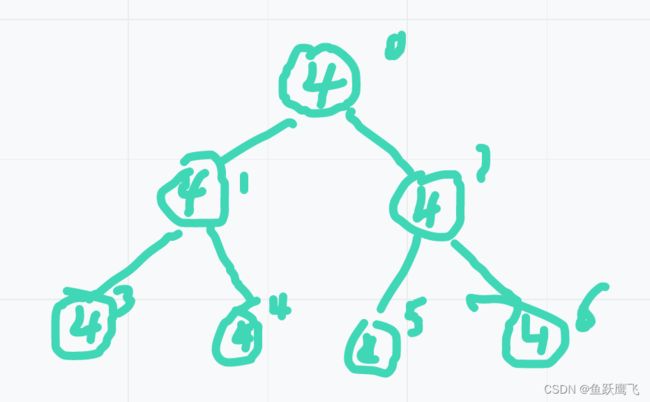
堆排序:完全保证不了稳定性,整体调成大根堆或者小根堆的过程就不稳定,比如数组是[4,4,4,4,4,4,4,4,6],前7个4插入结束后,堆是这样的:
当最后一个6来了之后需要先跟3交换,然后和1交换,然后和0交换
原数组中1位置的4跑到了2位置之后,3位置的4跑到了4,5,6之后
三种O(N * logN)的比较排序,如果追求速度用快排,因为
单纯追求速度使用快排:虽然时间复杂度是一样的,但是快排的常数时间更好
追求稳定性用归并:三个算法中唯一的稳定性算法
追求绝对的省空间适用堆排序:数组本身可以作为堆,用的只是有限几个变量
目前来说时间复杂度为O(N*logN),额外空间复杂度低于O(N)且稳定的基于比较的排序是不存在的。
Java自带的Arrays.sort的排序逻辑:
如果是基础类型,使用改进后的快排,因为基础类型排序,稳定性不重要而快排确实是最快的,时间常数最好的
如果是引用类型使用归并排序,也许稳定性不一定需要,但是未知的东西我们不能认为没有,只能考虑最差情况,为了保证稳定性,O(N*logN)只能用归并,且要保证相等时拷贝左边半区的元素
部分语言中会在快排的算法中写类似L + 60 < R使用插入排序的逻辑,这是因为虽然插入排序的时间复杂度是O(N^2),但是它的常数项更好,在数据量比较小的情况下插入排序执行时间可能小于快速排序,60是在长期实验条件下确定的值,这是工程上对于排序算法的改进。