Task01：基于逻辑回归的分类预测

• 逻辑回归模型的优劣势:

1. 优点：实现简单，易于理解和实现；计算代价不高，速度很快，存储资源低；
2. 缺点：容易欠拟合，分类精度可能不高

https://zhuanlan.zhihu.com/p/74874291

与 SVM

相同点

• 都是分类算法，本质上都是在找最佳分类超平面；
• 都是监督学习算法；
• 都是判别式模型，判别模型不关心数据是怎么生成的，它只关心数据之间的差别，然后用差别来简单对给定的一个数据进行分类；
• 都可以增加不同的正则项。

不同点

• LR 是一个统计的方法，SVM 是一个几何的方法；
• SVM 的处理方法是只考虑 Support Vectors，也就是和分类最相关的少数点去学习分类器。而逻辑回归通过非线性映射减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重；
• 损失函数不同：LR 的损失函数是交叉熵，SVM 的损失函数是 HingeLoss，这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。对 HingeLoss 来说，其零区域对应的正是非支持向量的普通样本，从而所有的普通样本都不参与最终超平面的决定，这是支持向量机最大的优势所在，对训练样本数目的依赖大减少，而且提高了训练效率；
• LR 是参数模型，SVM 是非参数模型，参数模型的前提是假设数据服从某一分布，该分布由一些参数确定（比如正太分布由均值和方差确定），在此基础上构建的模型称为参数模型；非参数模型对于总体的分布不做任何假设，只是知道总体是一个随机变量，其分布是存在的（分布中也可能存在参数），但是无法知道其分布的形式，更不知道分布的相关参数，只有在给定一些样本的条件下，能够依据非参数统计的方法进行推断。所以 LR 受数据分布影响，尤其是样本不均衡时影响很大，需要先做平衡，而 SVM 不直接依赖于分布；
• LR 可以产生概率，SVM 不能；
• LR 不依赖样本之间的距离，SVM 是基于距离的；
• LR 相对来说模型更简单好理解，特别是大规模线性分类时并行计算比较方便。而 SVM 的理解和优化相对来说复杂一些，SVM 转化为对偶问题后，分类只需要计算与少数几个支持向量的距离，这个在进行复杂核函数计算时优势很明显，能够大大简化模型和计算。

与线性回归的区别？

• 逻辑回归是在线性回归的基础上加了一个 Sigmoid 函数（非线形）映射，使得逻辑回归称为了一个优秀的分类算法。
• 本质上来说，两者都属于广义线性模型，但他们两个要解决的问题不一样，逻辑回归解决的是分类问题，输出的是离散值，线性回归解决的是回归问题，输出的连续值。

Sigmoid函数？

• 线性回归是在实数域范围内进行预测，而分类范围则需要在 [0,1]，逻辑回归减少了预测范围；
• 线性回归在实数域上敏感度一致，而逻辑回归在 0 附近敏感，在远离 0 点位置不敏感，这个的好处就是模型更加关注分类边界，可以增加模型的鲁棒性。

为什么需要归一化/取对数？为什么特征离散化后效果更好？

我们在使用逻辑回归的时候很少会把数据直接丢给 LR 来训练，我们一般会对特征进行离散化处理，这样做的优势大致有以下几点：

• 离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
• 离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；
• LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
• 离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；
• 特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化；

总的来说，特征离散化以后起到了加快计算，简化模型和增加泛化能力的作用。

1.Demo 实践

1.1 库函数导入

##  基础函数库 
import numpy as np 
## 导入画图库 
import matplotlib.pyplot as plt 
import seaborn as sns
## 导入逻辑回归模型函数 
from sklearn.linear_model import LogisticRegression

1.2 模型训练

##Demo演示LogisticRegression分类
## 构造数据集 
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]]) 
y_label = np.array([0, 0, 0, 1, 1, 1])
## 调用逻辑回归模型 
lr_clf = LogisticRegression()
## 用逻辑回归模型拟合构造的数据集 
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2

print(lr_clf)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)

print(x_fearures)

[[-1 -2]
 [-2 -1]
 [-3 -2]
 [ 1  3]
 [ 2  1]
 [ 3  2]]

x2=np.array([[-2,-5],[-1,3],[2,1],[6,7]])
c2=lr_clf.predict(x2)
x3=np.array([[1,2]])
c3=lr_clf.predict(x3)
print(c2)
print(c3)

[0 1 1 1]
[1]

1.3 模型参数查看

## 查看其对应模型的w 
print('the weight of Logistic Regression:',lr_clf.coef_)

## 查看其对应模型的w0 
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)

the weight of Logistic Regression: [[0.73455784 0.69539712]]
the intercept(w0) of Logistic Regression: [-0.13139986]

help(LogisticRegression)

1.4 数据和模型可视化

## 可视化构造的数据样本点

#plt.figure(num=None, figsize=None, dpi=None, facecolor=None, edgecolor=None, frameon=True)
#num:图像编号或名称，数字为编号 ，字符串为名称
#figsize:指定figure的宽和高，单位为英寸；
#dpi参数指定绘图对象的分辨率，即每英寸多少个像素，缺省值为80      1英寸等于2.5cm,A4纸是 21*30cm的纸张 
#facecolor:背景颜色
#edgecolor:边框颜色
#frameon:是否显示边框
plt.figure() 

#散点图
#plt.scatter(x, y, s, c ,marker, alpha)：x,y: x轴与y轴的数据
#s: 点的面积
#c: 点的颜色
#marker: 点的形状
#alpha: 透明度
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis') 

plt.title('Dataset') 
# 展示图标
plt.show()

# 可视化决策边界 
plt.figure() 
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis') 
plt.title('Dataset')

nx, ny = 200, 100
x_min, x_max = plt.xlim() 
y_min, y_max = plt.ylim() 
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))#生成网格点坐标矩阵

#predict是训练后返回预测结果，是标签值。
#predict_proba返回的是预测概率
#np.c_是按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等。类似于pandas中的merge()。
#np.r_是按列连接两个矩阵,就是把两矩阵上下相加,要求列数相等。类似于pandas中的concat()。
#numpy.ravel(): 将多维数组转换为一维数组
print(x_grid)
print(y_grid)
print(len(x_grid))
print(len(y_grid))
print(x_grid.shape)
print(y_grid.shape)
print(len(x_grid.ravel()))
print(len(y_grid.ravel()))
np.c_[x_grid.ravel(), y_grid.ravel()]


z_proba = lr_clf.predict_proba(np.c_[x_grid.ravel(), y_grid.ravel()]) 
z_proba = z_proba[:, 1].reshape(x_grid.shape) #shape是查看数据有多少行多少列 #reshape()是数组array中的方法，作用是将数据重新组织
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')#等高线图,contour画的是等高线中的线，而contourf画的是登高线之间的区域
plt.show()

[[-3.31161615 -3.27833358 -3.245051   ...  3.245051    3.27833358
   3.31161615]
 [-3.31161615 -3.27833358 -3.245051   ...  3.245051    3.27833358
   3.31161615]
 [-3.31161615 -3.27833358 -3.245051   ...  3.245051    3.27833358
   3.31161615]
 ...
 [-3.31161615 -3.27833358 -3.245051   ...  3.245051    3.27833358
   3.31161615]
 [-3.31161615 -3.27833358 -3.245051   ...  3.245051    3.27833358
   3.31161615]
 [-3.31161615 -3.27833358 -3.245051   ...  3.245051    3.27833358
   3.31161615]]
[[-2.2678858  -2.2678858  -2.2678858  ... -2.2678858  -2.2678858
  -2.2678858 ]
 [-2.21196891 -2.21196891 -2.21196891 ... -2.21196891 -2.21196891
  -2.21196891]
 [-2.15605203 -2.15605203 -2.15605203 ... -2.15605203 -2.15605203
  -2.15605203]
 ...
 [ 3.15605203  3.15605203  3.15605203 ...  3.15605203  3.15605203
   3.15605203]
 [ 3.21196891  3.21196891  3.21196891 ...  3.21196891  3.21196891
   3.21196891]
 [ 3.2678858   3.2678858   3.2678858  ...  3.2678858   3.2678858
   3.2678858 ]]
100
100
(100, 200)
(100, 200)
20000
20000

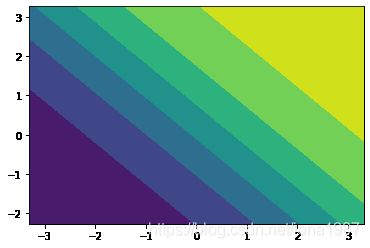
plt.contourf(x_grid, y_grid, z_proba)#等高线图,contour画的是等高线中的线，而contourf画的是等高线之间的区域
plt.show()

z_proba1 = lr_clf.predict(np.c_[x_grid.ravel(), y_grid.ravel()]) 
z_proba1 = z_proba1.reshape(x_grid.shape) #shape是查看数据有多少行多少列 #reshape()是数组array中的方法，作用是将数据重新组织
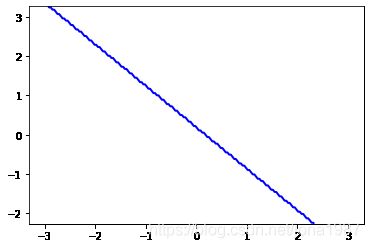
plt.contour(x_grid, y_grid, z_proba1, [0.5], linewidths=2., colors='blue')#等高线图,contour画的是等高线中的线，而contourf画的是登高线之间的区域
plt.show()

z_proba1 = lr_clf.predict(np.c_[x_grid.ravel(), y_grid.ravel()]) 
z_proba1 = z_proba1.reshape(x_grid.shape) #shape是查看数据有多少行多少列 #reshape()是数组array中的方法，作用是将数据重新组织
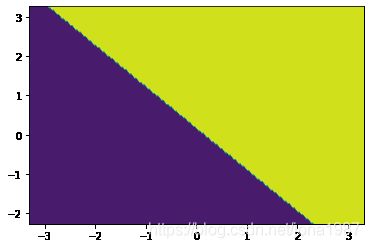
plt.contourf(x_grid, y_grid, z_proba1)#等高线图,contour画的是等高线中的线，而contourf画的是登高线之间的区域
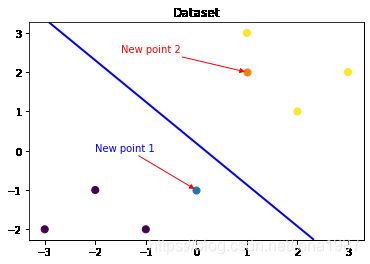
plt.show()

### 可视化预测新样本
plt.figure()

## new point 1 
x_fearures_new1 = np.array([[0, -1]]) 
plt.scatter(x_fearures_new1[:,0],x_fearures_new1[:,1], s=50, cmap='viridis') 
#Axes.annotate(s, xy, *args, **kwargs)      annotate用于在图形上给数据添加文本注解
#s：注释文本的内容
#xy：被注释的坐标点，二维元组形如(x,y)
#xytext：注释文本的坐标点，也是二维元组，默认与xy相同
#xycoords：被注释点的坐标系属性，允许输入的值如下
plt.annotate(s='New point 1',xy=(0,-1),xytext= (-2,0),color='blue',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))

## new point 2 
x_fearures_new2 = np.array([[1, 2]]) 
plt.scatter(x_fearures_new2[:,0],x_fearures_new2[:,1], s=50, cmap='viridis') 
plt.annotate(s='New point 2',xy=(1,2),xytext= (-1.5,2.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
## 训练样本 
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis') 
plt.title('Dataset')
# 可视化决策边界 
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')

plt.show()

1.5 模型预测

#predict是训练后返回预测结果，是标签值。
#predict_proba返回的是预测概率

## 在训练集和测试集上分布利用训练好的模型进行预测 
y_label_new1_predict = lr_clf.predict(x_fearures_new1) 
y_label_new2_predict = lr_clf.predict(x_fearures_new2)
print('The New point 1 predict class:\n',y_label_new1_predict) 
print('The New point 2 predict class:\n',y_label_new2_predict)
## 由于逻辑回归模型是概率预测模型（前文介绍的 p = p(y=1|x,\theta)）,所有我们可以利用 predict_proba 函数预测其概率 
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1) 
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)
print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba) 
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)

The New point 1 predict class:
 [0]
The New point 2 predict class:
 [1]
The New point 1 predict Probability of each class:
 [[0.69567724 0.30432276]]
The New point 2 predict Probability of each class:
 [[0.11983936 0.88016064]]

2 基于鸢尾花（iris）数据集的逻辑回归分类实践

2.1 库函数导入

# 基础函数库
import numpy as np
import pandas as pd

#绘图函数库
import matplotlib.pyplot as plt
import seaborn as sns

2.2 数据读取/载入

## 我们利用 sklearn 中自带的 iris 数据作为数据载入，并利用Pandas转化为DataFrame格式 
from sklearn.datasets import load_iris 
data = load_iris() #得到数据特征 
iris_target = data.target #得到数据对应的标签 
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为 DataFrame格式
print(type(iris_features))
print(iris_features)

     sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
0                  5.1               3.5                1.4               0.2
1                  4.9               3.0                1.4               0.2
2                  4.7               3.2                1.3               0.2
3                  4.6               3.1                1.5               0.2
4                  5.0               3.6                1.4               0.2
..                 ...               ...                ...               ...
145                6.7               3.0                5.2               2.3
146                6.3               2.5                5.0               1.9
147                6.5               3.0                5.2               2.0
148                6.2               3.4                5.4               2.3
149                5.9               3.0                5.1               1.8

[150 rows x 4 columns]

2.3 数据信息简单查看

## 利用.info()查看数据的整体信息 
iris_features.info()

RangeIndex: 150 entries, 0 to 149
Data columns (total 4 columns):
 #   Column             Non-Null Count  Dtype  
---  ------             --------------  -----  
 0   sepal length (cm)  150 non-null    float64
 1   sepal width (cm)   150 non-null    float64
 2   petal length (cm)  150 non-null    float64
 3   petal width (cm)   150 non-null    float64
dtypes: float64(4)
memory usage: 4.8 KB

## 进行简单的数据查看，我们可以利用 .head() 头部.tail()尾部 
iris_features.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

iris_features.tail()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
145	6.7	3.0	5.2	2.3
146	6.3	2.5	5.0	1.9
147	6.5	3.0	5.2	2.0
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8

## 其对应的类别标签为，其中0，1，2分别代表'setosa', 'versicolor', 'virginica'三种不同花的类别。 
iris_target

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

## 利用value_counts函数查看每个类别数量 
pd.Series(iris_target).value_counts()

2    50
1    50
0    50
dtype: int64

## 对于特征进行一些统计描述 
iris_features.describe()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
count	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.057333	3.758000	1.199333
std	0.828066	0.435866	1.765298	0.762238
min	4.300000	2.000000	1.000000	0.100000
25%	5.100000	2.800000	1.600000	0.300000
50%	5.800000	3.000000	4.350000	1.300000
75%	6.400000	3.300000	5.100000	1.800000
max	7.900000	4.400000	6.900000	2.500000

2.4 可视化描述

## 合并标签和特征信息 
iris_all = iris_features.copy() ##进行浅拷贝，防止对于原始数据的修改 
iris_all['target'] = iris_target

## 特征与标签组合的散点可视化 
#pairplot中pair是成对的意思，pairplot主要展现的是变量两两之间的关系 
# kind：用于控制非对角线上的图的类型，可选"scatter"与"reg"
# diag_kind：控制对角线上的图的类型，可选"hist"与"kde"
# hue ：针对某一字段进行分类
# palette：控制色调，如palette="husl"
# markers：控制散点的样式，如markers=["+", "s", "D"]
# vars,x_vars,y_vars：选择数据中的特定字段，以list形式传入，
# sns.pairplot(data,vars=["萼片长","花瓣长"]) 
# sns.pairplot(data,x_vars=["萼片长","花瓣宽"],
#              y_vars=["萼片宽","花瓣长"]) 
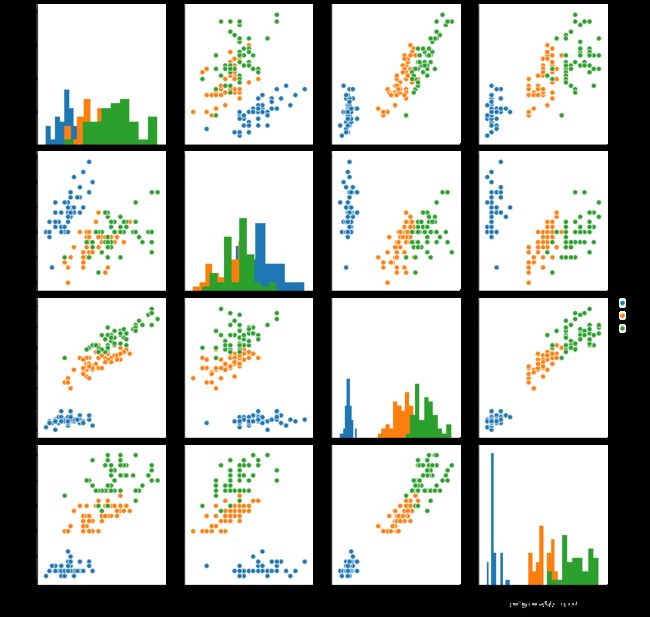
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
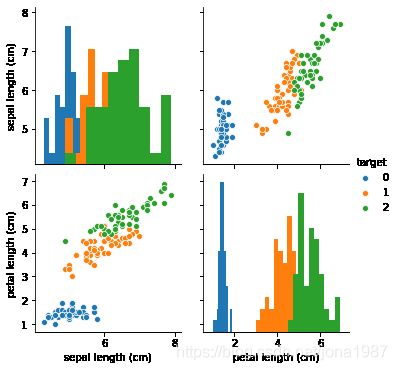
plt.show()

sns.pairplot(data=iris_all,vars=["sepal length (cm)","petal length (cm)"],diag_kind='hist', hue= 'target') 
plt.show()

# 箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。
# 它能显示出一组数据的最大值、最小值、中位数及上下四分位数。
# seaborn.boxplot(x=None, y=None, hue=None, data=None, order=None, hue_order=None, orient=None, color=None, 
#                 palette=None, saturation=0.75, width=0.8, dodge=True, fliersize=5, linewidth=None, 
#                 whis=1.5, notch=False, ax=None, **kwargs)
# x，y：dataframe中的列名（str）或者矢量数据
# data：dataframe或者数组
# palette：调色板，控制图像的色调
# hue（str）：dataframe的列名，按照列名中的值分类形成分类的条形图
# order, hue_order (lists of strings)：用于控制条形图的顺序
# orient："v"|"h" 用于控制图像使水平还是竖直显示（这通常是从输入变量的dtype推断出来的，此参数一般当不传入x、y，只传入data的时候使用）
# fliersize：float，用于指示离群值观察的标记大小
# whis： 确定离群值的上下界（IQR超过低和高四分位数的比例），此范围之外的点将被识别为异常值。IQR指的是上下四分位的差值。
# width： float，控制箱型图的宽度
for col in iris_features.columns: 
    sns.boxplot(x='target', y=col, saturation=0.5,palette='pastel', data=iris_all) 
    plt.title(col) 
    plt.show()
#利用箱型图我们也可以得到不同类别在不同特征上的分布差异情况

# 选取其前三个特征绘制三维散点图 
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(10,8)) 
#这些是作为单个整数编码的子绘图网格参数。
#例如，“111”表示“1×1网格，第一子图”，“234”表示“2×3网格，第四子图”。
ax = fig.add_subplot(111, projection='3d')

iris_all_class0 = iris_all[iris_all['target']==0].values 
iris_all_class1 = iris_all[iris_all['target']==1].values 
iris_all_class2 = iris_all[iris_all['target']==2].values # 'setosa'(0), 'versicolor'(1), 'virginica'(2) 
ax.scatter(iris_all_class0[:,0], iris_all_class0[:,1], iris_all_class0[:,2],label='setosa') 
ax.scatter(iris_all_class1[:,0], iris_all_class1[:,1], iris_all_class1[:,2],label='versicolor') 
ax.scatter(iris_all_class2[:,0], iris_all_class2[:,1], iris_all_class2[:,2],label='virginica') 
plt.legend()

plt.show()

print(iris_all_class0)

[[5.1 3.5 1.4 0.2 0. ]
 [4.9 3.  1.4 0.2 0. ]
 [4.7 3.2 1.3 0.2 0. ]
 [4.6 3.1 1.5 0.2 0. ]
 [5.  3.6 1.4 0.2 0. ]
 [5.4 3.9 1.7 0.4 0. ]
 [4.6 3.4 1.4 0.3 0. ]
 [5.  3.4 1.5 0.2 0. ]
 [4.4 2.9 1.4 0.2 0. ]
 [4.9 3.1 1.5 0.1 0. ]
 [5.4 3.7 1.5 0.2 0. ]
 [4.8 3.4 1.6 0.2 0. ]
 [4.8 3.  1.4 0.1 0. ]
 [4.3 3.  1.1 0.1 0. ]
 [5.8 4.  1.2 0.2 0. ]
 [5.7 4.4 1.5 0.4 0. ]
 [5.4 3.9 1.3 0.4 0. ]
 [5.1 3.5 1.4 0.3 0. ]
 [5.7 3.8 1.7 0.3 0. ]
 [5.1 3.8 1.5 0.3 0. ]
 [5.4 3.4 1.7 0.2 0. ]
 [5.1 3.7 1.5 0.4 0. ]
 [4.6 3.6 1.  0.2 0. ]
 [5.1 3.3 1.7 0.5 0. ]
 [4.8 3.4 1.9 0.2 0. ]
 [5.  3.  1.6 0.2 0. ]
 [5.  3.4 1.6 0.4 0. ]
 [5.2 3.5 1.5 0.2 0. ]
 [5.2 3.4 1.4 0.2 0. ]
 [4.7 3.2 1.6 0.2 0. ]
 [4.8 3.1 1.6 0.2 0. ]
 [5.4 3.4 1.5 0.4 0. ]
 [5.2 4.1 1.5 0.1 0. ]
 [5.5 4.2 1.4 0.2 0. ]
 [4.9 3.1 1.5 0.2 0. ]
 [5.  3.2 1.2 0.2 0. ]
 [5.5 3.5 1.3 0.2 0. ]
 [4.9 3.6 1.4 0.1 0. ]
 [4.4 3.  1.3 0.2 0. ]
 [5.1 3.4 1.5 0.2 0. ]
 [5.  3.5 1.3 0.3 0. ]
 [4.5 2.3 1.3 0.3 0. ]
 [4.4 3.2 1.3 0.2 0. ]
 [5.  3.5 1.6 0.6 0. ]
 [5.1 3.8 1.9 0.4 0. ]
 [4.8 3.  1.4 0.3 0. ]
 [5.1 3.8 1.6 0.2 0. ]
 [4.6 3.2 1.4 0.2 0. ]
 [5.3 3.7 1.5 0.2 0. ]
 [5.  3.3 1.4 0.2 0. ]]

2.5 利用逻辑回归模型在二分类上进行训练和预测

## 我们利用 sklearn 中自带的 iris 数据作为数据载入，并利用Pandas转化为DataFrame格式 
import pandas as pd
from sklearn.datasets import load_iris 
data = load_iris() #得到数据特征 
iris_target = data.target #得到数据对应的标签 
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为 DataFrame格式

## 为了正确评估模型性能，将数据划分为训练集和测试集，并在训练集上训练模型，在测试集上验证模型性能。 
from sklearn.model_selection import train_test_split
## 选择其类别为0和1的样本 （不包括类别为2的样本）
# loc方法：army.loc[['Arizona'], ['deaths']].在index的标bai签上进du行索引,范围包括zhistart和end。
# iloc方法：army.iloc[[0],[2]].在index的位置上进行索引,不包括end.
# ix 是 iloc 和 loc的合体。
iris_features_part = iris_features.iloc[:100] 
iris_target_part = iris_target[:100]
## 测试集大小为20%， 80%/20%分 
x_train, x_test, y_train, y_test = train_test_split(iris_features_part, iris_target_part, test_size = 0.2, random_state = 2020)
## 从sklearn中导入逻辑回归模型 
from sklearn.linear_model import LogisticRegression
## 定义 逻辑回归模型 
clf = LogisticRegression(random_state=0, solver='lbfgs')
# 在训练集上训练逻辑回归模型 
clf.fit(x_train, y_train)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=0, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)

## 查看其对应的w 
print('the weight of Logistic Regression:',clf.coef_)
## 查看其对应的w0 
print('the intercept(w0) of Logistic Regression:',clf.intercept_)

the weight of Logistic Regression: [[ 0.45181973 -0.81743611  2.14470304  0.89838607]]
the intercept(w0) of Logistic Regression: [-6.53367714]

## 在训练集和测试集上分布利用训练好的模型进行预测 
train_predict = clf.predict(x_train) 
test_predict = clf.predict(x_test)

from sklearn import metrics

## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果 
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict)) 
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

## 查看混淆矩阵 (预测值和真实值的各类情况统计矩阵) 
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test) 
print('The confusion matrix result:\n',confusion_matrix_result)

# 利用热力图对于结果进行可视化 
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(4, 3)) 
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues') 
plt.xlabel('Predicted labels') 
plt.ylabel('True labels') 
plt.show()

The accuracy of the Logistic Regression is: 1.0
The accuracy of the Logistic Regression is: 1.0
The confusion matrix result:
 [[ 9  0]
 [ 0 11]]

2.6 :利用逻辑回归模型在三分类(多分类)上进行训练和预测

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
data=load_iris()
iris_features=pd.DataFrame(data=data.data,columns=data.feature_names)
iris_target=data.target

## 测试集大小为20%， 80%/20%分 
x_train, x_test, y_train, y_test = train_test_split(iris_features, iris_target, test_size = 0.2, random_state = 2020)
## 定义 逻辑回归模型 
clf = LogisticRegression(random_state=0, solver='lbfgs')
# 在训练集上训练逻辑回归模型 
clf.fit(x_train, y_train)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=0, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)

## 查看其对应的w 
print('the weight of Logistic Regression:\n',clf.coef_)
## 查看其对应的w0 
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)
## 由于这个是3分类，所有我们这里得到了三个逻辑回归模型的参数，其三个逻辑回归组合起来即可实现三分类

the weight of Logistic Regression:
 [[-0.45928925  0.83069892 -2.26606529 -0.99743983]
 [ 0.33117319 -0.72863426 -0.06841147 -0.98711029]
 [ 0.12811606 -0.10206466  2.33447676  1.98455011]]
the intercept(w0) of Logistic Regression:
 [  9.43880649   3.93047365 -13.36928015]

## 在训练集和测试集上分布利用训练好的模型进行预测 
train_predict = clf.predict(x_train) 
test_predict = clf.predict(x_test)
## 由于逻辑回归模型是概率预测模型（前文介绍的 p = p(y=1|x,\theta)）,所有我们可以利用 predict_proba 函数预测其概率 
train_predict_proba = clf.predict_proba(x_train) 
test_predict_proba = clf.predict_proba(x_test)
print('The test predict Probability of each class:\n',test_predict_proba) 
## 其中第一列代表预测为0类的概率，第二列代表预测为1类的概率，第三列代表预测为2类的概率。

from sklearn import metrics
## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果 
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict)) 
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

The test predict Probability of each class:
 [[1.03461743e-05 2.33279482e-02 9.76661706e-01]
 [9.69926591e-01 3.00732871e-02 1.21677013e-07]
 [2.09992555e-02 8.69156613e-01 1.09844131e-01]
 [3.61934879e-03 7.91979964e-01 2.04400687e-01]
 [7.90943229e-03 8.00605296e-01 1.91485271e-01]
 [7.30034944e-04 6.60508053e-01 3.38761912e-01]
 [1.68614215e-04 1.86322047e-01 8.13509339e-01]
 [1.06915328e-01 8.90815535e-01 2.26913684e-03]
 [9.46928073e-01 5.30707271e-02 1.20016067e-06]
 [9.62346387e-01 3.76532214e-02 3.91897321e-07]
 [1.19533394e-04 1.38823471e-01 8.61056996e-01]
 [8.78881872e-03 6.97207354e-01 2.94003827e-01]
 [9.73938144e-01 2.60617331e-02 1.22613846e-07]
 [1.78434059e-03 4.79518175e-01 5.18697484e-01]
 [5.56924354e-04 2.46776840e-01 7.52666235e-01]
 [9.83549843e-01 1.64500657e-02 9.13617315e-08]
 [1.65201472e-02 9.54672748e-01 2.88071049e-02]
 [8.99853765e-03 7.82707573e-01 2.08293890e-01]
 [2.98015042e-05 5.45900078e-02 9.45380191e-01]
 [9.35695860e-01 6.43039548e-02 1.85301396e-07]
 [9.80621191e-01 1.93787393e-02 7.00125323e-08]
 [1.68478824e-04 3.30167230e-01 6.69664291e-01]
 [3.54046184e-03 4.02267802e-01 5.94191736e-01]
 [9.70617285e-01 2.93824721e-02 2.42443984e-07]
 [2.56895220e-04 1.54631584e-01 8.45111520e-01]
 [3.48668505e-02 9.11966137e-01 5.31670124e-02]
 [1.47218858e-02 6.84038109e-01 3.01240005e-01]
 [9.46510498e-04 4.28641988e-01 5.70411501e-01]
 [9.64848138e-01 3.51516743e-02 1.87917904e-07]
 [9.70436781e-01 2.95624007e-02 8.18591667e-07]]
The accuracy of the Logistic Regression is: 0.9833333333333333
The accuracy of the Logistic Regression is: 0.8666666666666667

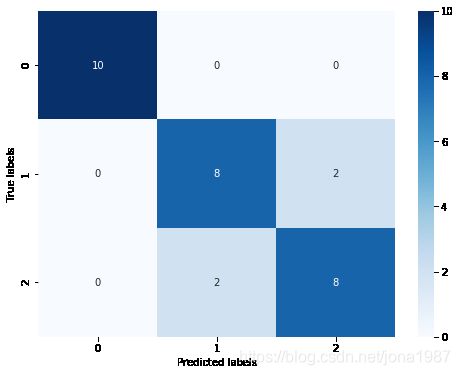
## 查看混淆矩阵 
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test) 
print('The confusion matrix result:\n',confusion_matrix_result)

import matplotlib.pyplot as plt
import seaborn as sns
# 利用热力图对于结果进行可视化 
plt.figure(figsize=(8, 6)) 
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues') 
plt.xlabel('Predicted labels') 
plt.ylabel('True labels') 
plt.show()

The confusion matrix result:
 [[10  0  0]
 [ 0  8  2]
 [ 0  2  8]]

逻辑回归参数详细说明

以下内容摘自 https://www.jianshu.com/p/58359008b6b0

LogisticRegression，一共有14个参数,参数说明如下：

1. penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布，所谓的范式就是加上对参数的约束，使得模型更不会过拟合(overfit)，但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。
2. dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
3. tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
4. c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。
5. fit_intercept：是否存在截距或偏差，bool类型，默认为True。
6. intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。
7. class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者’balanced’字符串，默认为不输入，也就是不考虑权重，即为None。如果选择输入的话，可以选择balanced让类库自己计算类型权重，或者自己输入各个类型的权重。举个例子，比如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。如果class_weight选择balanced，那么类库会根据训练样本量来计算权重。某种类型样本量越多，则权重越低，样本量越少，则权重越高。当class_weight为balanced时，类权重计算方法如下：n_samples / (n_classes * np.bincount(y))。n_samples为样本数，n_classes为类别数量，np.bincount(y)会输出每个类的样本数，例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]。

那么class_weight有什么作用呢？

在分类模型中，我们经常会遇到两类问题：

第一种是误分类的代价很高。比如对合法用户和非法用户进行分类，将非法用户分类为合法用户的代价很高，我们宁愿将合法用户分类为非法用户，这时可以人工再甄别，但是却不愿将非法用户分类为合法用户。这时，我们可以适当提高非法用户的权重。

第二种是样本是高度失衡的，比如我们有合法用户和非法用户的二元样本数据10000条，里面合法用户有9995条，非法用户只有5条，如果我们不考虑权重，则我们可以将所有的测试集都预测为合法用户，这样预测准确率理论上有99.95%，但是却没有任何意义。这时，我们可以选择balanced，让类库自动提高非法用户样本的权重。提高了某种分类的权重，相比不考虑权重，会有更多的样本分类划分到高权重的类别，从而可以解决上面两类问题。

8. random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。
9. solver：优化算法选择参数，只有五个可选参数，即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是：

liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。

lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。

saga：线性收敛的随机优化算法的的变重。

10. max_iter：算法收敛最大迭代次数，int类型，默认为10。仅在正则化优化算法为newton-cg, sag和lbfgs才有用，算法收敛的最大迭代次数。

11. multi_class：分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr。ovr即前面提到的one-vs-rest(OvR)，而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。

12. verbose：日志冗长度，int类型。默认为0。就是不输出训练过程，1的时候偶尔输出结果，大于1，对于每个子模型都输出。

13. warm_start：热启动参数，bool类型。默认为False。如果为True，则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化）。

14. n_jobs：并行数。int类型，默认为1。1的时候，用CPU的一个内核运行程序，2的时候，用CPU的2个内核运行程序。为-1的时候，用所有CPU的内核运行程序。

solver总结

• liblinear适用于小数据集，而sag和saga适用于大数据集因为速度更快。
• 对于多分类问题，只有newton-cg,sag,saga和lbfgs能够处理多项损失，而liblinear受限于一对剩余(OvR)。啥意思，就是用liblinear的时候，如果是多分类问题，得先把一种类别作为一个类别，剩余的所有类别作为另外一个类别。一次类推，遍历所有类别，进行分类。
• newton-cg,sag和lbfgs这三种优化算法时都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的L1正则化，只能用于L2正则化。而liblinear和saga通吃L1正则化和L2正则化。
• 同时，sag每次仅仅使用了部分样本进行梯度迭代，所以当样本量少的时候不要选择它，而如果样本量非常大，比如大于10万，sag是第一选择。但是sag不能用于L1正则化，所以当你有大量的样本，又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量，要么回到L2正则化。
• 从上面的描述，大家可能觉得，既然newton-cg, lbfgs和sag这么多限制，如果不是大样本，我们选择liblinear不就行了嘛！错，因为liblinear也有自己的弱点！我们知道，逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR，不支持MvM，这样如果我们需要相对精确的多元逻辑回归时，就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。

OvR和MvM有什么不同？

• OvR的思想很简单，无论你是多少元逻辑回归，我们都可以看做二元逻辑回归。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推。
• 而MvM则相对复杂，这里举MvM的特例one-vs-one(OvO)作讲解。如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。
• 可以看出OvR相对简单，但分类效果相对略差（这里指大多数样本分布情况，某些样本分布下OvR可能更好）。而MvM分类相对精确，但是分类速度没有OvR快。如果选择了ovr，则4种损失函数的优化方法liblinear，newton-cg,lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。

总结：

• 优点：实现简单，易于理解和实现；计算代价不高，速度很快，存储资源低。
• 缺点：容易欠拟合，分类精度可能不高。
• 其他：

Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数，求解过程可以由最优化算法完成。

改进的一些最优化算法，比如sag。它可以在新数据到来时就完成参数更新，而不需要重新读取整个数据集来进行批量处理。

机器学习的一个重要问题就是如何处理缺失数据。这个问题没有标准答案，取决于实际应用中的需求。现有一些解决方案，每种方案都各有优缺点。

我们需要根据数据的情况，这是Sklearn的参数，以期达到更好的分类效果。