因果推断18--估计个体治疗效果:泛化界和算法CRF(个人笔记)
目录
1. 介绍
2. 相关工作
3.估计ITE:误差界
4. 估计ITE的算法
5.实验
5.1. 模拟结果:IHDP
5.2. 现实世界的结果:工作
5.3. 结果
6.结论
参考
英文题目:Estimating individual treatment effect: generalization bounds and algorithms
翻译:估计个体治疗效果:泛化界和算法
论文链接:http://proceedings.mlr.press/v70/shalit17a/shalit17a.pdf
代码:
Pytorch版本
GitHub - patrickzoechbauer/TarNet
Tensorflow版本
GitHub - arnaud39/TARNet: TARNet Model with tensorflow 2 API.
摘要:人们对将机器学习应用于医疗保健、经济学和教育等领域的因果推理问题非常感兴趣。特别是,个人级别的因果推断具有重要的应用,例如精度医学。我们提出了一个新的理论分析和算法系列,用于从观察数据中预测个体治疗效应 (ITE),假设称为强可想象性。该算法学习“平衡”表示,使得诱导处理和控制分布看起来相似,并且我们给出了一种新颖的直观泛化误差界限,表明表示的预期 ITE 估计误差受该表示的标准泛化误差之和以及由表示引起的处理和控制分布之间的距离。我们使用整体概率度量来衡量分布之间的距离,推导出 Wasserstein 和最大平均差异 (MMD) 距离的显式界限。对真实数据和模拟数据的实验表明,新算法匹配或优于最先进的算法。
1. 介绍
对动作因果影响进行预测是许多领域中的一个核心问题。例如,决定哪种药物会对患者带来更好的结果的医生;政府决定谁将从资助的工作培训中受益最多;或者决定哪个研究计划最能使特定学生受益的教师。在本文中,我们专注于根据观察数据进行这些预测的问题。观察数据是包含过去动作、他们的结果以及可能更多上下文的数据,但没有直接访问产生动作的机制。例如,我们可以访问患者(上下文)、他们的药物(动作)和结果的记录,但我们没有完全了解为什么将特定动作应用于患者。
从观察数据中学习的标志是,在数据中观察到的动作取决于可能影响结果的变量,从而导致混淆:例如,更丰富的患者可能更好地提供某些药物,并且只能将工作培训提供给那些动机足以寻求它。挑战在于如何解开这些混杂因素并进行有效的预测。具体来说,我们在“无隐藏混淆”的常见简化假设下工作,假设观察到确定采取哪些动作的所有因素。在上面的示例中,这意味着我们测量了患者的财富或员工的动机。
作为一个学习问题,从观测数据估计因果效应与经典学习不同,因为在我们的训练数据中,我们从未看到个体层面的效应。对于每个单元,我们只看到它们对可能动作之一的响应——它们实际收到的动作。这接近于机器学习文献中已知的“从记录的老虎机反馈中学习”(Strehl 等人,2010;Swaminathan 和 Joachims,2015),不同之处在于我们无法访问模型生成动作的模型。
我们的工作与因果推理的许多工作不同,因为我们专注于个人层面的因果效应(“特定治疗效果”Shpitser & Pearl (2006);Pearl (2015)),而不是平均或人口水平。我们的主要贡献是给出据我们所知,第一个用于估计个体水平因果效应的泛化误差 1 界限,其中每个个体由其特征 x 识别。该界限自然导致了一系列新的基于表示学习的算法(Bengio 等人,2013 年),我们表明在几个因果效应推理任务上匹配或优于最先进的方法。
两个分布 p(x|t = 0) 和 p(x|t = 1) 之间距离的积分概率度量 (IPM) 度量,也称为控制和处理分布。在实践中,我们使用两个特定的IPMs:最大平均差异(Gretton和Wasserstein距离(Villani, 2008;Cuturi & Doucet, 2014)。我们表明,学习个体治疗效果函数 τ (x) 的预期误差上限为学习 Y1 和 Y0 的误差加上 IPM 项。在随机对照试验设置中,其中t⊥⊥x,IPM项为0,我们的界自然简化为学习两个函数的标准学习问题。
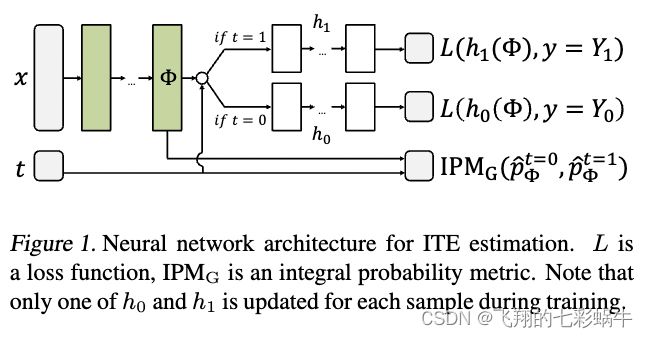
我们根据表示学习的思想推导出一系列算法的方法(Bengio et al., 2013):在最小化事实损失的加权和的表示之上联合学习处理和控制的假设(标准监督机器学习目标),以及表示引起的控制和处理分布之间的 IPM 距离。这可以被视为在鼓励在治疗组和对照组之间更好的泛化的约束下学习函数 m0 和 m1。在实验中,我们应用基于神经网络的算法作为表示和假设,以及表示层的 MMD 或 Wasserstein 分布距离;有关基本架构,请参见图 1。
在他关于因果关系的基本文本中,Pearl (2009) 写道:“与传统学习任务一样,我们尝试从一组实例推广到另一组实例,因果建模任务是从一组条件下的行为推广到 [...] 另一组。因此,因果模型应该由一个挑战它们对不断变化的条件稳定性的标准来选择[强调我们的]。我们相信我们的工作指出了一种这样的稳定性标准的方法,用于在强可忽略的情况下进行因果推理。
2. 相关工作
用于因果推理的机器学习的许多工作都集中在因果发现上,目的是从数据中发现潜在的因果图或因果方向(Hoyer 等人,2009;Maathuis 等人,2010;Triantafillou 和 Tsamardinos,2015;Mooij 等人,2016)。我们专注于因果设置简单且已知的形式为 (Y1, Y0) ⊥ x|t 且没有隐藏混杂因素的情况。在因果模型下,我们假设 ap- 中使用的因果效应推理最常见的目标隐含科学是获得平均处理效果:AT E = Ex∼p(x) [τ (x)]。我们将简要讨论一些标准的统计因果效应推理方法如何与我们提出的方法相关。请注意,这些方法中的大多数都假设某种形式的可学习性。
另一种广泛使用的因果效应推断统计方法家族是加权方法。逆倾向评分加权(Austin, 2011)等方法对观测数据中的单元进行加权,使处理后的种群和控制种群更具可比性,并也被用于估计条件效应(Cole et al., 2003)。主要挑战,特别是在高维情况下,是控制估计的方差(Swaminathan & Joachims,2015)。双鲁棒方法更进一步,巧妙地结合倾向评分重加权和协变量调整来减少模型偏差(Funk et al., 2011)。
特别是,估计 ITE 需要预测与观察到的分布不同的结果。我们的ITE误差上限与BenDavid等人(2007)给出的领域适应的泛化界限有相似之处;Mansour等人(2009);Ben-David等人(2010);Cortes & Mohri(2014)。这些界限采用分布距离度量,例如 A 距离或差异度量,这些指标与我们使用的 IPM 距离有关。我们的算法类似于Ganin等人(2016)最近的域适应算法,原则上其他域适应方法(如Dauḿe III(2007);Pan等人(2011);Sun等人(2016))可以适应用于ITE估计,如这里所示。
最后,我们的论文建立在Johansson等人(2016)的基础上,在Johansson等人(2016)中,我们展示了协变量移位与估计反事实的任务之间的联系。我们提出了学习数据的表示,使处理和控制分布更相似,在其之上拟合线性岭回归模型。我们使用反向处理分配的分布与使用事实分布拟合岭回归来限制拟合岭回归的相对误差。不幸的是,相对误差界限并不是关于表示的绝对质量的所有信息。在本文中,我们专注于一个相关但更实质性的任务:估计个体治疗效果,建立在反事实误差项之上。我们提供了表示绝对质量的信息界限。我们还推导出更灵活的算法家,包括非线性假设和更强大的分布度量,以 Wasserstein 和 MMD 距离等 IPM 的形式。最后,我们进行了更彻底的实验,包括真实数据集和样本外性能,并表明我们的方法优于先前提出的方法。
// 论文的基本模式
3.估计ITE:误差界
在本节中,我们证明了估计给定表示的单个治疗效果的预期误差以及在该表示上定义的假设的边界。该界限用 (1) 将观察到的结果 y 学习为 x 和 t 的函数时模型的预期损失表示为 (1),表示为 <F , F 代表“事实”; (2) 处理组和对照组分布之间的积分概率度量 (IPM) 距离。术语푡是经典的机器学习泛化误差,反过来可以使用经验误差和模型复杂性项的上限,应用标准机器学习理论(Shalev-Shwartz&Ben-David,2014)。
4. 估计ITE的算法
我们提出了一个基于上述理论结果的ITE估计通用框架CFR(反事实回归)。我们的算法是一个端到端的正则化最小化过程,它既适合数据的平衡表示,又适合结果的假设。CFR 借鉴了与我们之前的工作相同的直觉(Johansson 等人,2016 年),但克服了以下限制:a)我们之前的理论需要一个两步优化过程,并且特定于线性假设(不支持例如深度神经网络),b)如果学习的表示是高维的,则治疗指标可能会在旧模型中洗掉(见下文讨论)。
5.实验
评估因果推理算法比许多机器学习任务更难,因为我们很少可以访问基本事实治疗效果。现有的文献主要以两种方式处理这一点。一种是使用(半)合成数据集,其中结果或治疗分配是完全已知的;我们使用来自 Hill (2011) 的半合成 IHDP 数据集。另一种是使用来自随机对照试验 (RCT) 的真实世界数据。使用来自 RCT 的数据的问题是治疗组之间没有不平衡,这使得我们的方法变得多余。我们通过使用 LaLonde (1986) 中的 Jobs 数据集来部分克服这个问题,该数据集包括随机和非随机组件。我们使用这两个组件进行训练,但仅使用随机组件进行评估。这减轻了但无法解决,完全随机和平衡的数据集不适合我们的方法的问题。
5.1. 模拟结果:IHDP
5.2. 现实世界的结果:工作
5.3. 结果
6.结论
在本文中,我们给出了一个有意义和直观的误差界来估计个体治疗效果。我们的界限将 ITE 估计与从样本中学习的经典机器学习问题联系起来,以及测量样本分布距离的方法。该界限自然适用于学习算法的创建;我们专注于使用神经网络作为表示和假设。我们将我们的理论引导方法应用于合成和真实任务,表明在每种情况下,我们的方法都匹配或优于最先进的方法。重要的开放性问题是选择 IPM 权重 α 的理论考虑因素,如何最好地推导出模型预测的置信度区间,并将我们的工作与更复杂的因果模型(例如具有隐藏混淆或工具变量的模型)相结合。
参考
- 果推断17--基于反事实因果推断的度小满额度模型学习笔记_飞翔的七彩蜗牛的博客-CSDN博客
- 因果推断|反事实推断|经典论文解读|TargetNet&CFR模型-基于表示学习 - 知乎