「分治法」最大子段和问题

一、问题描述

给定由n个整数组成的序列(a1, a2, …, an)，最大子段和问题要求该序列形如∑ak (i <= k <= j) 的最大值（1≤i≤j≤n）。

当序列中所有整数均为负整数时，定义最大子段和为0。例如，序列(-20, 11, -4, 13, -5, -2)的最大子段和为11 - 4 + 13 = 20。

{5,-3,4,2}的最大子序列是 {5,-3,4,2}，它的和是8,达到最大；{5,-6,4,2}的最大子序列是{4,2}，它的和是6。

注意，要求这个子段必须是连续的。

二、问题分析

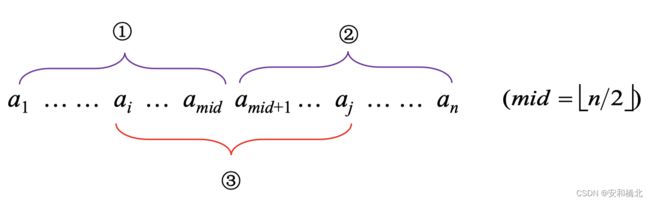
首先还是采用分治的方法，将该序列分成相等的两端，然后递归的求出左边的最大子段和以及右边的最大子段和。

但是这个就会出现和上一题“最近点对距离”一样的问题：如果最大子段和不是在左右两边，而是在中间怎么办？也就是上图3的部分。

那么也就意味着，我们进行子问题的划分之后，还是会出现三种情况：

1. 最大子段和是左边的最大子段和
2. 最大子段和是左边的最大子段和
3. 最大子段和是中间部分的最大子段和

所以也就导出了我们的解决方法：先递归求解情况1和2，然后再单独处理问题3。

三、算法设计

#include 
using namespace std;

int maxSum(int a[],int left,int right) {
    int sum = 0;
    if(left == right) 
    {
        if(a[left] > 0) sum = a[left];
        else sum = 0;
    } 
    else // 递归体
    {
        int center = (left + right) / 2;
        int leftsum = maxSum(a, left, center);
        int rightsum = maxSum(a, center + 1, right);

        int s1 ,lefts = 0;
        for(int i = center ; i >= left; i--) {
            lefts += a[i];
            if(lefts > s1) s1 = lefts;
        }
        int s2 ,rights = 0;
        for(int i = center + 1 ; i <= right; i++) {
            rights += a[i];
            if(rights > s2) s2 = rights;
        }

        sum = s1 + s2;
        if(sum < leftsum) sum = leftsum;
        if(sum < rightsum) sum = rightsum;    
    } 
    return sum;
}

int main() {
    int a[6] = {-20, 11, -4, 13, -5, -2};
    int res = maxSum(a,0,5);
    cout<<"-------------"<<endl;
    cout<<res<<endl;
}

四、代码分析

在这里简单记录一下自己对本次代码的递归思路：

1. 首先整个MaxSum方法就是一个递归方法，因此既然是递归方法，就必须要有结束条件，必须要有if语句。
2. 而if语句里面的内容，往往是递归到最后的基本情况。对于本题来说，就是划分到只有一个一个元素的时候，就可以直接求取最大子段和了，就是这个数本身。
3. 然后就是最主要的部分：递归体的内容。
   1. 首先就是划分，划分完之后，直接写两个递归体的内容
      leftsum=MaxSum(a, left, center); //对应情况①，递归求解 rightsum=MaxSum(a, center+1, right); //对应情况②，递归求解
   2. 然后就是对应的特殊情况3。解释一下情况3的思路：就是分别求出来左右两边的最大子段和然后加起来，作为情况3的最大子段和。
4. 那么递归的过程呢？拿最开始的完整的序列为例：
   1. 进入方法后，if判断不满足，然后进入递归体。
   2. 划分为两半，然后进入左边的递归。
   3. 进入左边的递归后，可能还是不满足if判断，然后继续进入划分后的左边的递归。
   4. 一直到左边被划分成了只有一个元素，然后进入if判断，把答案给leftsum。然后返回上一层的递归。
   5. 返回到上一层的递归后，再执行右边的递归。这个时候右边的递归可以认为也是只有一个元素，因为每次都是按中间来划分的。然后也是把答案给rightsum。
   6. 接下来就到了情况3了。此时就要看看是左右两边的大还是中间的大，谁大就返回谁的值。