【NLP】KMP匹配算法

一、说明

      KMP算法。也称为Knuth-Morris-Pratt字符串查找算法可在一个字符串S内查找一个词W的出现位置。一个词在不匹配时本身就包含足够的信息来确定下一个匹配可能的开始位置，此算法利用这一特性以避免重新检查先前配对的字符。将时间复杂度从O(M*N)降为O(N).

        这个算法由高德纳和沃恩·普拉特在1974年构思，同年詹姆斯·H·莫里斯也独立地设计出该算法，最终三人于1977年联合发表。

二、不使用KMP算法查找过程描述

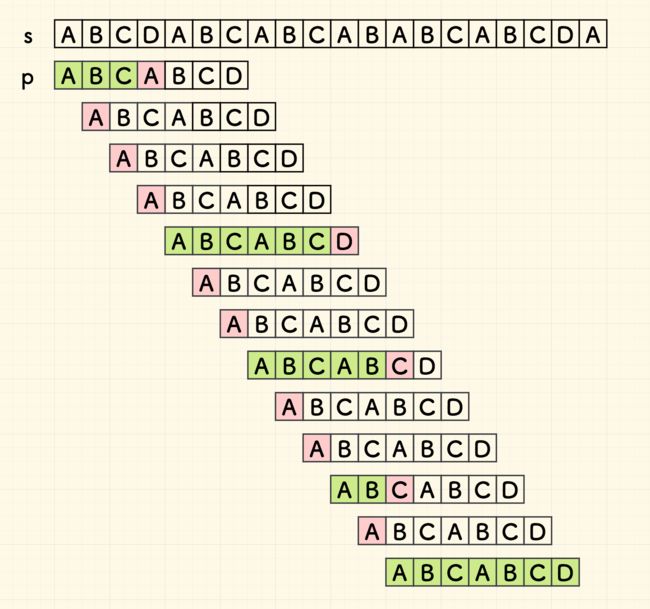
        我们将从S字符串中，查找P字段的位置。为了方便，我们将S叫做【文本】，将P叫做【模式】，整个查询过程如下图所示：

图1 从文本中查找字段的暴力查询

从以上查询中，我们不难看出，有许多多余的查询操作是不必要的。举例如下：

        既然ABC是匹配的，那么字段p的首字A与BCD重复地做了三次比较，而这三次比较的结果完全可以不依赖文本S的信息，单从P的内部就可以预测，A与{BCD}比较，其比较一定不匹配。因此，这三次比较多余。

三、如何提高搜索比较的效率

3.1 当字段内部无内部匹配的搜索

        什么叫“字段内无内部匹配”？就是字段p内无重复的字符。

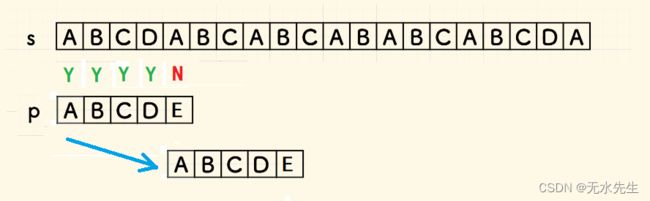
        字段内没有重复的字符如p=【ABCDE】，与文本s匹配，这里假定文本是【ABCDABCABCABABCABCDA】，其匹配过程如下：

         显然，当出现前缀ABCD匹配，而到E的时候不匹配，p可以立刻跳到E当前的位置，将继续实行匹配。因为有前提“字段内无内部匹配”，因此，A后面没有A存在，也就无需匹配。

3.2 当字段内部有内部匹配的搜索

将以上的字段进行改变，p=【ABCAE】重复上面操作，效果图如下：

        可以看到，当E出现不匹配的时候，比较明智的跳转方法是，下次匹配发生在E的前一个位置，因为这里的A与字段首部存在一个匹配。

        直观地看出，要想去除不必要的匹配，有必要研究不匹配E前边的前缀字段。

四、前缀表的构想

        对于能否减少匹配的时间，关键要对模式进行研究。对于模式而言，其内部匹配决定了匹配模式如何移动。前人对于模式的研究，我们产生了前缀表这样的数据结构。本节我们试图应用一个前缀表，至于它如何构造，在后文中揭示。

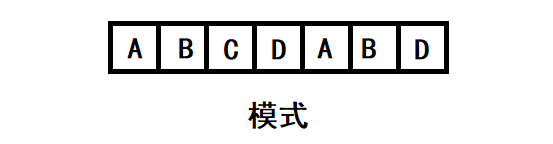
        假定我们有如下字符模式：

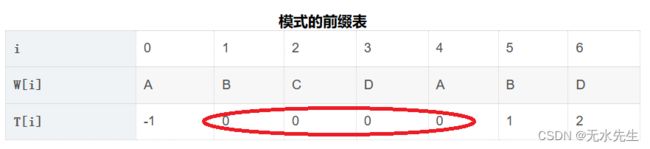
 将以上模式做成如下表格，

模式的前缀表

i	0	1	2	3	4	5	6
W[i]	A	B	C	D	A	B	D
T[i]	-1	0	0	0	0	1	2

        朋友们可能不知道如何使用这个表格，那么我们将演示如何应用这个表格。

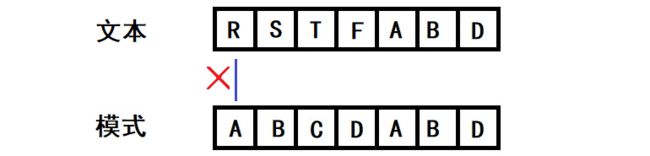
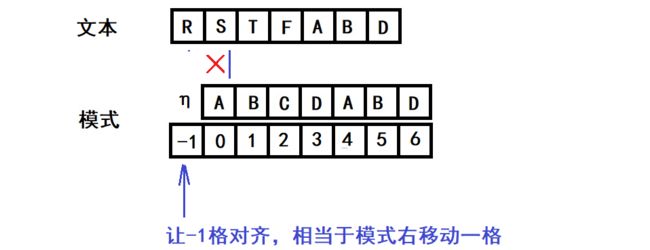
1）当第一个字符就不匹配怎么办？

        上图显然R-A不匹配，模式将移到下一个字符继续匹配，也就是模式的“-1”位置对齐到R的位置，继续下一轮匹配。  

        继续以后，S-A也不匹配，模式继续右移动...总之，所有的与模式第一个字符不匹配，就让模式的-1位置对齐，从模式的“0”位置继续匹配。这就是A对应-1的意义。

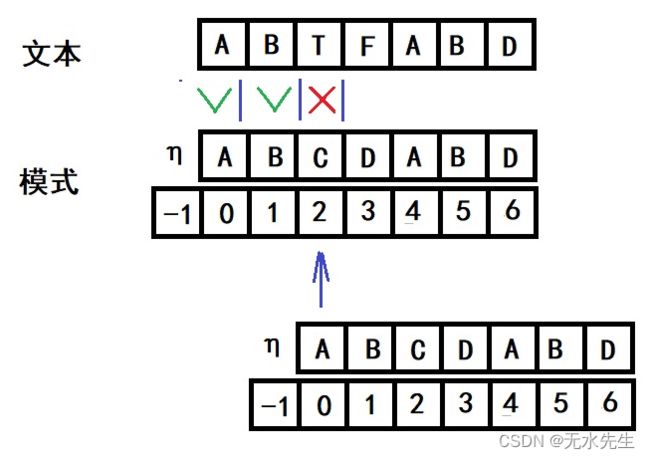
2）当第二个字符不匹配怎么办？

        当第一个字符匹配成功后，如何进行呢？继续下一个字符的匹配。如下图：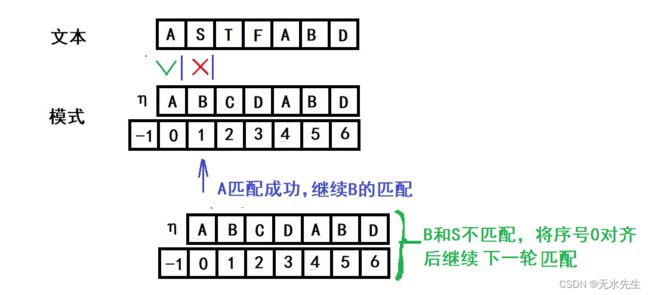

        第三个字符不匹配，如何继续？同样，将首段（0序号）移到该位置继续匹配。

        

 以此类推，表格中的  BCDA如果不匹配，都一样处理。

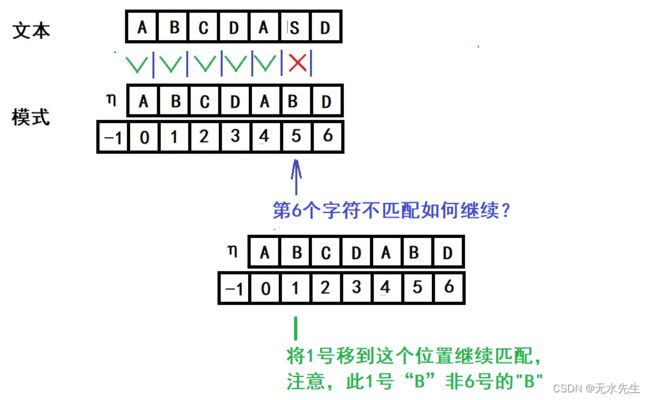
 3）当第六个字符不匹配怎么办？

 

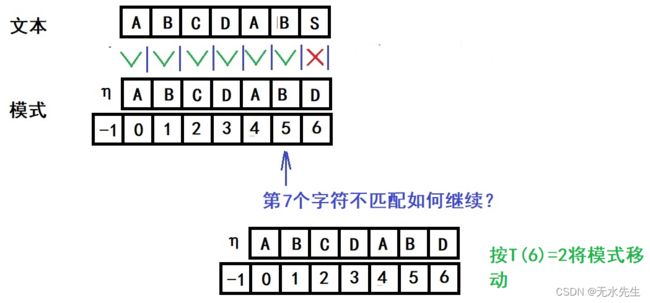
  4）当第七个字符不匹配怎么办？

 

五、前缀表的构建法

5.1 前缀表构建原则

构建前缀表遵守下列原则：

1.   只考虑模式内部结构，不考虑文本的结构。
2.   只考虑模式中，哪一位字符不匹配，对于匹配的情况不考虑。
3.   当模式第i位发生不匹配时，从[0, i-1] 位字段分析
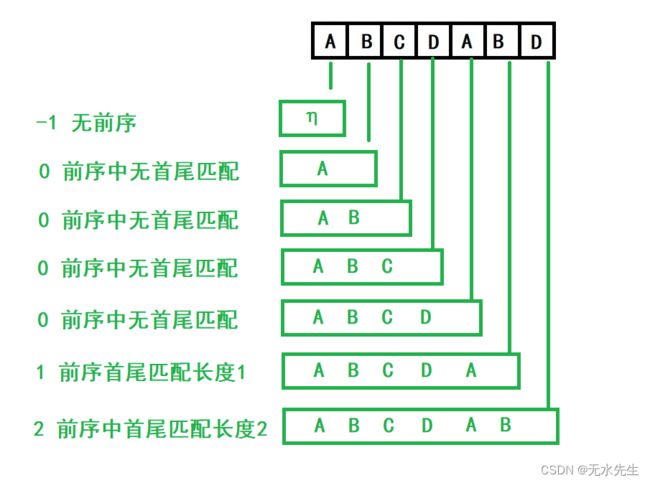
4.   对于【0，i-1】位字段，看其最大首尾匹配列，最大首尾匹配长度，正是前缀表的偏移T(i)

什么是最大首尾匹配？

就是形如：

 

 5.2 实现一个具体例子

        因此，构造前缀表的依据如图所示：

六、前缀表代码实现

        提供一组KMP的实现算法，请大家自行测试：

# Python program for KMP Algorithm
def KMPSearch(pat, txt):
	M = len(pat)
	N = len(txt)

	# create lps[] that will hold the longest prefix suffix
	# values for pattern
	lps = [0]*M
	j = 0 # index for pat[]

	# Preprocess the pattern (calculate lps[] array)
	computeLPSArray(pat, M, lps)

	i = 0 # index for txt[]
	while i < N:
		if pat[j] == txt[i]:
			i += 1
			j += 1

		if j == M:
			print ("Found pattern at index", str(i-j))
			j = lps[j-1]

		# mismatch after j matches
		elif i < N and pat[j] != txt[i]:
			# Do not match lps[0..lps[j-1]] characters,
			# they will match anyway
			if j != 0:
				j = lps[j-1]
			else:
				i += 1

def computeLPSArray(pat, M, lps):
	len = 0 # length of the previous longest prefix suffix

	lps[0] # lps[0] is always 0
	i = 1

	# the loop calculates lps[i] for i = 1 to M-1
	while i < M:
		if pat[i]== pat[len]:
			len += 1
			lps[i] = len
			i += 1
		else:
			# This is tricky. Consider the example.
			# AAACAAAA and i = 7. The idea is similar
			# to search step.
			if len != 0:
				len = lps[len-1]

				# Also, note that we do not increment i here
			else:
				lps[i] = 0
				i += 1

txt = "ABABDABACDABABCABAB"
pat = "ABABCABAB"
KMPSearch(pat, txt)

# This code is contributed by Bhavya Jain