【svopro】代码梳理
- SVO2系列之深度滤波DepthFilter
- svo_note
- SVO(SVO: fast semi-direct monocular visual odometry)
- SVO 半直接视觉里程计
- 【DepthFilter】深度滤波器
- 【svopro】代码梳理
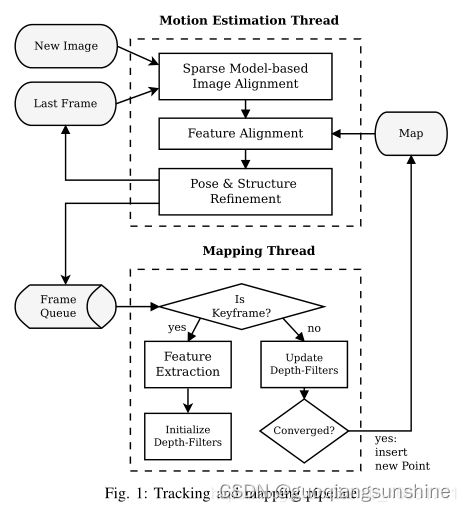
svo processFrame代码梳理
-
-
- 1.0 processFrame主流程
- 1.1 sparseImageAlignment
-
- 1.1.1 核心实现:
- 1.1.2 输入输出与更新全局变量:
- 1.2 projectMapInFrame
-
- 1.2.1 实现步骤:
- 1.2.2 输入输出与更新全局变量:
- 1.3 optimizeStructure
-
- 1.3.1 主接口输入输出与更新全局变量:
- 1.3.2 核心接口实现:
- 1.3.3 FrameHandlerBase::optimizePose接口输入输出与更新全局变量:
- 1.3.4 PoseOptimizer::run算法步骤:
- 1.3.5 位姿优化(重投影误差)PoseOptimizer::run接口输入输出与更新全局变量:
- 1.3.6 三维点优化 FrameHandlerBase::optimizeStructure接口算法步骤
- 1.4 关键帧的生成
-
- 1.4.1 关键帧的生成步骤
- 1.4.2 生成关键帧的主要条件如下:
- 1.4.3 关键帧的生成接口输入输出与更新全局变量:
- 1.5. problem
-
- 1.5.1 两个主要问题:
- 1.5.2 关于种子点更新
- 1.5.3 关键帧插入条件判断
-
1.0 processFrame主流程
UpdateResult FrameHandlerStereo::processFrame()
直接法具体过程如下:
step1. 准备工作。假设相邻帧之间的位姿 T k , k − 1 T_{k,k−1} Tk,k−1已知,一般初始化为上一相邻时刻的位姿或者假设为单位矩阵。通过之前多帧之间的特征检测以及深度估计,我们已经知道第k-1帧中特征点位置以及它们的深度。
step2. 重投影。知道 I k − 1 I_{k−1} Ik−1中的某个特征在图像平面的位置(u,v),以及它的深度d,能够将该特征投影到三维空间 p k − 1 p_{k−1} pk−1,该三维空间的坐标系是定义在 I k − 1 I_{k−1} Ik−1摄像机坐标系的。所以,我们要将它投影到当前帧 I k I_{k} Ik中,需要位姿转换 T k , k − 1 T_{k,k−1} Tk,k−1,得到该点在当前帧坐标系中的三维坐标 p k p_k pk。最后通过摄像机内参数,投影到 I k I_{k} Ik的图像平面 ( u ′ , v ′ ) (u′,v′) (u′,v′),完成重投影。
step3. 迭代优化更新位姿 。按理来说对于空间中同一个点,被极短时间内的相邻两帧拍到,它的亮度值应该没啥变化。但由于位姿是假设的一个值,所以重投影的点不准确,导致投影前后的亮度值是不相等的。不断优化位姿使得这个残差最小,就能得到优化后的位姿 T k , k − 1 T_{k,k−1} Tk,k−1。
将上述过程公式化如下:通过不断优化位姿 T k , k − 1 T_{k,k−1} Tk,k−1最小化残差损失函数。其优化函数为:
T k − 1 k = a r g m i n ∬ ℜ ρ [ δ I ( T , u ) ] d u T_{k−1}^k=argmin∬_ℜρ[δI(T,u)]du Tk−1k=argmin∬ℜρ[δI(T,u)]du
其中:
ρ [ ∗ ] = 0.5 ∥ ∗ ∥ 2 ρ[∗]=0.5∥∗∥^ 2 ρ[∗]=0.5∥∗∥2,可见整个过程是一个最小二乘法的问题;
δ I ( T , u ) = I k ( π ( T ∗ π − 1 ( u , d u ) ) ) − I k − 1 ( u ) δI ( T , u ) = I _k(π ( T* π ^{− 1} ( u , d u ) )) − I k − 1 ( u ) δI(T,u)=Ik(π(T∗π−1(u,du)))−Ik−1(u),这个残差对比的是图像位置上的像素值的灰度,其中u ∈ ℜ ,ℜ表示即可以在k-1帧图像上看到,又可以通过投影在k帧上看到
对于比对灰度值的算法来说,一般都会用一个patch size中的全部像素的灰度进行对比,因此下面的公式中都不仅仅使用一点像素,而是使用多点像素进行求解的,但是在这个过程中,作者为了提高计算的速度,并没有进行patch的投影,算是以量取胜吧
NOTE:公式中 π − 1 ( u , d u ) π ^{− 1} ( u , d u ) π−1(u,du) 为根据图像位置和深度逆投影到三维空间,第二步 T ∗ π − 1 ( u , d u ) T* π ^{− 1} ( u , d u ) T∗π−1(u,du) 将三维坐标点旋转平移到当前帧坐标系下,第三步 π ( T ∗ π − 1 ( u , d u ) ) π ( T* π ^{− 1} ( u , d u ) ) π(T∗π−1(u,du)) 再将三维坐标点投影回当前帧图像坐标。当然在优化过程中,残差的计算方式不止这一种形式:有前向(forwards),逆向(inverse)之分,并且还有叠加式(additive)和构造式(compositional)之分。这方面可以读读光流法方面的论文,Baker的大作《Lucas-Kanade 20 Years On: A Unifying Framework》。选择的方式不同,在迭代优化过程中计算雅克比矩阵的时候就有差别,一般为了减小计算量,都采用的是inverse compositional algorithm。
优化目标函数:
把上述的notation带入到优化函数中就可以得到
T k − 1 k = a r g m i n ∑ i ∈ ℜ 1 / 2 ∥ δ I ( T k − 1 k , u i ) ∥ 2 T_{k−1}^k=argmin∑_{i∈ℜ}1/2∥δI(T_{k−1}^k,u_i)∥^2 Tk−1k=argmini∈ℜ∑1/2∥δI(Tk−1k,ui)∥2
其中雅克比矩阵为图像残差对李代数的求导,可以通过链式求导得到:
J = ∂ δ I ( ξ , u i ) ∂ ξ = ∂ I k − 1 ( a ) ∂ a ∣ a = u i . ∂ π ( b ) ∂ b ∣ b = p i . ∂ T ( ξ ) ∂ ξ ∣ ξ = 0 . p i = ∂ I ∂ u . ∂ u ∂ b . ∂ b ∂ ξ J=\frac{\partial\delta I(\xi,u_i)}{\partial\xi} = \frac{\partial I_{k-1}(a)}{\partial a}|_{a=u_{i}}.\frac{\partial π(b)}{\partial b}|_{b =p_{i}}.\frac{\partial T(\xi)}{\partial \xi}|_{\xi=0}.p_i = \frac{\partial I}{\partial u}. \frac{\partial u}{\partial b}. \frac{\partial b}{\partial \xi} J=∂ξ∂δI(ξ,ui)=∂a∂Ik−1(a)∣a=ui.∂b∂π(b)∣b=pi.∂ξ∂T(ξ)∣ξ=0.pi=∂u∂I.∂b∂u.∂ξ∂b
对于上一帧的每一个特征点,都进行这样的计算, 在自己本来的层数上, 取那个特征点左上角的 4x4 图块。如果特征点映射回原来的层数时,坐标不是整数,就进行插值,其实,本来提取特征点的时候,在这一层特征点坐标就应该是整数。把图块往这一帧的图像上的对应的层数投影,然后计算雅克比和残差。 计算残差时, 因为投影的位置并不刚好是整数的像素,所以会在投影点附近插值,获取与投影图块对应的图块。最后,得到一个巨大的雅克比矩阵,以及残差矩阵。但是为了节省存储空间,提前就转换成了 H 矩阵 $ H =J *J ^ T$ 。
上面的非线性最小化二乘问题,可以用高斯牛顿迭代法求解,位姿的迭代增量ξ(李代数)可以通过下述方程计算:
J T J ξ = − J T δ I ( 0 ) H ξ = − J T δ I ( 0 ) ξ = − H − 1 J T δ I ( 0 ) J^TJξ =-J^T \delta I(0) \\ H \xi=-J^T \delta I(0) \\ \xi =-H^{-1}J^T \delta I(0) \\ JTJξ=−JTδI(0)Hξ=−JTδI(0)ξ=−H−1JTδI(0)
然后,得到 T ( ξ ) T(\xi) T(ξ) ,逆矩阵得到 T ( ψ ) T(\psi) T(ψ) ,再更新出 T k , k − 1 T_{k,k-1} Tk,k−1 。然后,在新的位置上,再从像素点坐标,投影出新的点 p k − 1 p_{k-1} pk−1。每一层迭代 30 次。 因为这种 inverse-compositional 方法,用这种近似的思想,雅克比就可以不用再重新计算了。(因为重新投影出新的 p 点的位置, 这个过程没有在残差公式里面表现出来。) 这样子逐层下去,重复之前的步骤。
1.1 sparseImageAlignment
该函数的作用是使用稀疏光流法优化当前帧相对于前一帧之间的相机位姿。稀疏光流求解器通过在前一帧中选取一些特征点,并在新帧(当前帧)中寻找相应的特征点,从而做到优化相机位姿的效果。该过程的具体步骤如下:
- 重置和设置稀疏光流优化器,包括权重、最大要跟踪的特征数量等参数。
- 如果拥有运动先验,则将其应用于图像对齐(优化相机位姿)的过程中。该步骤可以通过添加加权先验项,将imu传感器的运动信息融合到图像对齐的过程中,从而增强优化估计的鲁棒性。
- 通过运行稀疏光流求解器,找到尽可能多的特征点,以优化相机位姿,并返回拥有匹配的特征点数。
- 返回匹配到特征点的数量。
1.1.1 核心实现:
size_t SparseImgAlign::run(const FrameBundle::Ptr &ref_frames,
const FrameBundle::Ptr &cur_frames)
该函数的作用是运行稀疏光流法进行图像对齐,即通过优化相机的相对运动来最大化场景中的特征点在两帧图像中的匹配程度。该过程的具体步骤如下:
- 检查并保证输入帧的有效性,获取其中的跟踪特征,并在必要时对其进行子采样。
- 设置必要的成员变量,例如当前帧、参考帧、参考帧相对于世界坐标系的位姿。
- 准备缓存以存储需要用到的中间变量,包括特征在两帧图像中的坐标(像素坐标)和空间中的位置(3D坐标),两帧图像之间的采样点之间的雅可比矩阵等。其中有一些变量可以在多个金字塔层次上共享使用,以加速算法的运行速度。
- 在金字塔的每一层上,先计算一些预处理的通用变量。然后使用LM算法对特征点进行优化,最终得到两帧之间最佳的像素级对齐结果。
- 将优化后的结果保存,并返回被跟踪的特征点数。
1.1.2 输入输出与更新全局变量:
输入:- ref_frames:指向参考帧的指针,存储了参考帧中的特征点和图像信息。
- cur_frames:指向当前帧的指针,存储了当前帧中的特征点和图像信息。
输出:- n_fts_to_track:表示成功跟踪的特征点数。
-
在该函数的主体结构中,更新了以下几个全局变量:
- ref_frames_:参考帧。
- cur_frames_:当前帧。
- T_iref_world_:参考帧的imu坐标系到世界坐标系之间的变换。
- uv_cache_:特征点在两帧图像中的像素坐标,作为缓存提高运行效率。
- xyz_ref_cache_:特征点在参考帧中的3D空间坐标,作为缓存提高运行效率。
- jacobian_proj_cache_:两帧图像之间的采样点之间的雅可比矩阵,作为缓存提高运行效率。
- alpha_init_:初始化的亮度增益。
- beta_init_:初始化的亮度偏移。
- level_:当前运行所在的金字塔等级。
- mu_:LM算法中的缩放因子。
- have_cache_:一个布尔变量,用于表示是否已经准备好计算雅可比矩阵的缓存。
1.2 projectMapInFrame
函数的作用是在帧中投影地图(包含3D点和特征),并在图像中搜索匹配的特征。该过程的具体步骤如下:
计算有重叠的关键帧,以便后续在这些帧中搜索匹配特征。
如果启用了异步重投影,则为每个相机启动一个异步重投影任务,实现并行处理。
否则,为每个相机执行投影任务
reprojectors_.at(camera_idx)->reprojectFrames(frame, overlap_kfs_.at(camera_idx), trash_points.at(camera_idx));
删除对于某一相机而言不再视野范围内的3D点,释放内存。
统计所有重投影器的匹配特征总数,并根据特定约束来判断是否匹配特征数量是否满足要求。
返回匹配特征的总数。
1.2.1 实现步骤:
该函数的作用是向当前帧中重新投影3D地图点,从而找到匹配的二维特征点,以便在后续的位姿估计和优化中使用。实现中,函数首先将输入的相邻关键帧中的所有3D地图点与当前帧进行投影匹配,并将候选匹配点的相应信息存储在一个候选列表candidates_中。然后,该函数通过一系列的筛选条件对候选匹配点进行过滤和排序,并找到其中最佳的匹配点,并计算这些点的重投影误差(Reprojection Error),并将其存储在栅格地图(Occupandy Grid)中以进行后续的处理。
具体实现步骤如下:
- 组合所有相邻关键帧中的有效3D地图点,并检查其有效性(是否超过最大重投影次数、是否足够成熟、是否已被标记为Outlier等)。
- 将有效的3D地图点投影到2D图像平面上,并得到对应的2D特征点,将其保存到一个候选列表candidates_中。
- 根据候选列表中的2D特征点,检查它们是否与当前帧中的2D特征点重叠,若重叠,则进行匹配。
- 对匹配结果进行排序,并筛选最优的匹配结果。同时更新栅格地图中的区域占用情况,以避免在后续的迭代中提取过多的新特征点。如果特征点数已达到阈值,则结束投影过程。
1.2.2 输入输出与更新全局变量:
输入:
- cur_frame: 当前帧,带有以下信息:
- 相机内参矩阵K和畸变矩阵distortion
- 当前帧的id、世界坐标系下的位姿、2D特征点和对应的描述子等信息。
- visible_kfs: 相邻关键帧的列表。
- trash_points: 需要删除的3D地图点的列表,超出最大重投影次数或观测次数太少的3D地图点属于垃圾。
- max_n_fixed_lm: 从全局地图中选择的最大不可变地标数目。
- max_total_n_features: 当前帧可以使用的最大特征点个数,其中包括当前帧计算出来的点,以及从相邻关键帧中反投影得到的点的个数之和。
输出:
- 无。
更新的全局变量:
- candidates_: 存储在栅格化坐标系中的候选匹配列表(Candidate),其中包括从相邻关键帧中投影得到的匹配点和已经估计出的3D地图点。
- 栅格地图(Occupandy Grid): 记录每个栅格中是否有特征点、是否被访问过等信息,用于后续的特征点更新和位姿估计等操作。
- trash_points: 需要删除的3D地图点的列表。
1.3 optimizeStructure
该函数的作用是通过最小化各个特征点在不同关键帧之间的投影误差,以优化场景中所有的3D点的空间坐标。该过程的具体步骤如下:
- 获取所有关键帧(frames)中的所有特征点,筛选出需要优化的特征点。特定的筛选条件为:该特征点必须有对应的3D点,并且不能是边缘点。
- 根据空间坐标,对于所有待优化的3D点,运用LM算法进行优化,获取其在空间中的最优坐标。
- 更新每个3D点上一次被优化的时间。
- 返回优化完成时,被优化的3D点数量。
1.3.1 主接口输入输出与更新全局变量:
输入: frames: 存储有所有关键帧的指针。
输出:该函数没有明确的输出,但是在函数内部有一些全局变量被更新,包括:
- 所有3D点的空间坐标将被优化,并更新其优化的时间戳(last_structure_optim_)。
1.3.2 核心接口实现:
size_t FrameHandlerBase::optimizePose()
该函数的作用是**对于所有帧(当前时刻对应的frame_bundle对应的观测),在全局范围内优化它们的相对位姿,即在不同图像帧之间找到特征点的对应关系以计算相机位置姿态**。该过程的具体步骤如下:
- 重置位姿优化器(pose_optimizer_),以便于从一个干净的状态开始对所有帧进行位姿优化。
- 如果有运动先验,则应用它们来约束该过程中优化的相机位姿,即通过在LM优化算法中添加先验权重的方式来衡量优化解决方案的可靠性。自我运动模型可以通过另一个数据流获得,也可以在相机的运动中进行模拟。
- 运行位姿优化器,以估计所有帧之间的相对位姿,并在过程中尽量减少特征点匹配之间的重投影误差。
- 在最后,返回优化后 SFBA 图中所有边的数量,表示优化解决方案中的约束数,用于求解相机位姿。
1.3.3 FrameHandlerBase::optimizePose接口输入输出与更新全局变量:
输入:该函数无任何输入。
输出:- sfba_n_edges_final:表示在位姿优化过程中使用的边的数量,用于表明位姿优化解决方案的约束数量。
更新了的全局变量:
该函数主要使用了位姿优化器(pose_optimizer_),对所有的帧进行优化,以更新帧之间的相对位姿。位姿优化过程可能会产生一个新的SFBA图,但这个图是保存在优化器内部的,而不是在函数之外的类中。因此,该函数没有明确更新全局变量的行为。
1.3.4 PoseOptimizer::run算法步骤:
size_t PoseOptimizer::run(const FrameBundle::Ptr &frame_bundle,
double reproj_thresh_px)
该函数的作用是运行Gauss-Newton优化算法,**对输入的关键帧bundle中的所有帧进行位姿优化,以计算每个帧之间的相对位姿,从而使得所有3D点的投影误差最小化。**该过程的具体步骤如下:
- 检查输入的帧是否满足要求,如果无法进行计算,则直接返回。
- 获取第一个帧的IMU到世界坐标系中的变换(T_imu_world),用于初始求解。
- 根据初始值计算初始状态下的误差,得到初始的测量方差(measurement_sigma_)。
- 使用Gauss-Newton算法对所有帧的相对位姿进行优化,使得重投影误差最小化。
- 将每个帧在世界坐标系下的位姿设置为相机到世界坐标系的转换矩阵(frame->T_f_w_ = frame->T_cam_imu() * T_imu_world)。
- 移除重投影误差较大的噪点,并计算剩余边的数量。
1.3.5 位姿优化(重投影误差)PoseOptimizer::run接口输入输出与更新全局变量:
输入:
- frame_bundle:存储有所有关键帧的数据集指针。
- reproj_thresh_px:重投影误差阈值,用于剔除噪点。
输出:
- 优化后剩余边的数量,返回值减去被移除的边的数量。
更新了的全局变量:
- focal_length_:库伯恩-图克法测量的初始值标度长度.
- frame_bundle_:输入的关键帧束指针。
- T_imu_world: 表示第一个帧IMU到世界坐标系的变换。
- measurement_sigma_:估计的初始测量方差。
- n_meas_:测量(边)的总数。
1.3.6 三维点优化 FrameHandlerBase::optimizeStructure接口算法步骤
void FrameHandlerBase::optimizeStructure(
const FrameBundle::Ptr &frames, int max_n_pts, int max_iter)
该函数的**作用是对3D点进行优化**。在优化过程中,使用多种观测作为约束条件来估计点的位置,从而提高点的位置精度。同时,通过最小化重投影误差,使点能更好地适应相机移动和姿态变化。具体来说,该函数采用LM算法或者高斯-牛顿法来迭代计算点的位置xyz坐标。每迭代一次,都计算一组新的重投影误差,更新雅克比矩阵、梯度向量,直到误差足够小或者达到迭代上限时停止。
此函数中使用的优化算法可以采用高斯-牛顿法或Levenberg-Marquardt算法等。其中包括两个重要步骤:
1.计算重投影误差: 遍历之前所有观测到该特征点的帧,计算投影点和特征点之间的误差(或描述为残差,如unit plane residual)。如果采用透视相机模型,则使用透视变换将特征点从相机坐标系转换到世界坐标系中,并在每个观测点处计算预测值,并以此计算重投影误差。
2.更新雅克比矩阵: 为了计算优化方程,需要计算雅克比矩阵(或描述为导数矩阵)。雅可比矩阵的元素由重投影误差对点位置的偏导数计算而来。
在计算过程中,需要对新误差进行比较并更新点的位置。如果重投影误差有所增加或更新后的点位置不满足优化要求,则需要撤销更新前的点位置。
1.4 关键帧的生成
UpdateResult FrameHandlerStereo::makeKeyframe()
1.4.1 关键帧的生成步骤
该函数用于决定当前帧是否需要成为新的关键帧,并且如果需要成为关键帧,则执行以下操作:
- 如果当前帧的特征点数低于下限阈值(kfselect_numkfs_lower_thresh),则增加特征点数量,将相邻关键帧的一个帧作为新的关键帧,将所有新特征点加入到地图中,并进行三角化。
- 选择当前帧作为新的关键帧,将其加入到地图中,将当前帧的所有新特征点加入到地图中。
- 初始化新的深度滤波器、并将其与相应的特征检测器绑定,将当前帧中已经提取出的特征点对应的栅格置为已占用状态,将当前帧加入到深度滤波器中。
- 根据相邻关键帧协助进行新特征点的深度滤波(Depth Filter)更新。
- 如果当前地图中关键帧数量已经达到极限,则删除距离当前帧最远的关键帧(使用Ceres优化时,区别对待地图的删除操作)。
该函数的输出是一个枚举类型UpdateResult,代表着新一个新的关键帧已经被选定。
1.4.2 生成关键帧的主要条件如下:
- 当前帧距离上一个关键帧的时间超过设定的阈值,即时间间隔超过options_.keyframe_min_rot、options_.keyframe_min_trans、options_.keyframe_min_inliers 中的任意一个。
- 当前帧到与上一个关键帧的重叠帧(Overlapping frames)之一的运动量大于设定的阈值 options_.keyframe_max_overlap_R、options_.keyframe_max_overlap_t。
- 当前有足够的2D特征点符合基础矩阵假设,即当前帧中符合基础矩阵投影约束的2D特征点数量需要达到 options_.keyframe_min_features个。
其中,条件(1)和(2)是为了控制关键帧之间的密度,防止在时间或空间上有大量的冗余关键帧。同时,条件(2)也是为了保证运动的光滑性,避免给VO模型带来过多的噪声。条件(3)则是为了保证特征点的分布均匀和数量合理。需要注意的是,除了这些条件之外,还可能会有其他条件:例如,当**当前帧与所有已有地图点的距离太远时,也可以将其作为关键帧以增加地图的范围。
1.4.3 关键帧的生成接口输入输出与更新全局变量:
输入:
- new_frames_: 存储最新帧信息的指针,包括当前帧和相邻关键帧。
- overlap_kfs_: 存储当前帧与最新相邻关键帧之间的重叠帧(Overlapping frames)列表。
- depth_filter_: 深度滤波器,用于更新3D点的深度估计。
- map_: 地图,存储关键帧和3D点等信息。
- bundle_adjustment_type_: 前端图优化的类型,目前主要支持两种优化算法:Ceres和g2o。
- options_: 系统参数类,包括多种系统参数,如特征点数量下限、生成关键帧条件等。
输出:
- 返回一个枚举类型UpdateResult,代表着新一个新的关键帧已经被选定。
更新的全局变量:
- map_: 将新的关键帧加入到地图中,并更新与相邻关键帧的关系。
- depth_filter_: 将当前帧和相邻关键帧添加到深度滤波器中,并更新3D点的深度估计。
- candidates_: 存储在栅格化坐标系中的候选匹配列表(Candidate),其中包括从相邻关键帧中投影得到的匹配点和已经估计出的3D地图点。
- 栅格地图(Occupandy Grid): 记录每个栅格中是否有特征点、是否被访问过等信息,用于后续的特征点更新和位姿估计等操作。
1.5. problem
1.5.1 两个主要问题:
- 关键帧选择:当前,只有当移动距离达到场景平均深度的15%时,才会选择关键帧。如果相机朝向前方,则场景深度非常大,并且不会选择新的关键帧。
- 种子点更新:向前移动时,种子点的收敛速度不够快,因为视差非常小。问题在于,我们仅使用新种子点(seeds)创建之后的帧更新种子点。对于向前拍摄的相机,这是可以的,因为早期的帧尚未观察到该表面。但是,对于向前拍摄的相机,我们也应使用旧的关键帧来更新种子点。
1.5.2 关于种子点更新
将N个最近或重叠关键帧添加到新帧的深度滤波器中的困难是什么?
在DepthFilter中一次性添加多个关键帧(如新帧及其最近的N个关键帧)需要解决诸多问题:
- 关键帧的数量:将N个最接近的关键帧添加进去需要考虑深度滤波器队列(queue)中能存放的关键帧的数量限制。队列中存放的关键帧数量多了,可能会增加计算负担,而数量太少则会减慢3D点深度收敛的速度。
- 关键帧之间的距离:例如,有一组新的关键帧,其中有些关键帧越近,则其视角下的图像内容差别较小,它们之间的深度读数可以相互帮助更快地收敛(seed 合并)。
- 帧之间的时间和大小:如果在关键帧之间差异很大,例如,相机姿态变化剧烈或场景遮挡很大,那么不同帧之间可能会产生很大的不一致性,导致更高的滤波误差。因此需要选择时间尺度类似、帧大小相似的关键帧来更新种子点。
- 代码复杂性:同时处理多个帧的数据往往需要更多的代码来管理程序复杂度,并且需要处理许多输入和输出数据的交互,而这些数据涉及多方面的运算,会增加代码难度和执行时间。
在代码中,首先使用setCoreKfs()函数设定了最近的3个重叠关键帧,把它们存储在core_kfs_ 中。然后把这个集合作为参数传给DepthFilter的updateSeeds()函数用于对新帧种子点的更新。优先级方面,可以按照一定的规则确定要使用哪些最接近的关键帧。但需要注意的是,在添加新帧之前,必须确保队列中已经存储足够的关键帧来使得新帧具有足够多的观测信息以进行深度更新。
https://github.com/uzh-rpg/rpg_svo/blob/master/svo/src/frame_handler_mono.cpp#L191
1.5.3 关键帧插入条件判断
bool FrameHandlerBase::needNewKf(const Transformation &)
这个函数的作用是判断是否需要新的关键帧。该函数有一个输入参数Transformation&是当前帧与最近关键帧的位姿变换。在函数中,通过多种条件判断是否需要新的关键帧,这些条件可以在系统参数类(options_)中设置。如:
- 当前帧距离上一关键帧的时间大于设定的上限时间时,需要新的关键帧;
- 当前已匹配的特征点数量不足时,需要新的关键帧;
- 当前帧与最近关键帧的视差大于设定的最小视差时,需要新的关键帧;
- 当前帧与最近关键帧的角度和距离大于设定的阈值时,需要新的关键帧。
这个函数的输出结果是一个bool型的值,表示是否需要一个新的关键帧。如果需要,该函数返回值为true,否则为false。该函数是SLAM算法中一个非常重要的环节,控制关键帧的选取,保证系统的稳定性和速度。