K-means聚类算法（附Python实现代码）

一、K-means算法基本思想

1、基于划分的聚类

划分算法的思想是，将给定待挖掘数据集中的数据对象划分成K组（k≤N，N代表数据集中对象数目），每一组表示一个聚类的簇。并且要满足任何一个数据对象仅可以属于一个聚类，每个聚类中至少具有一个数据对象。
此算法通常要求算法开始之前，给定参数K以决定聚类后的聚类的个数。算法根据参数k建立一个初始的分组，以后算法反复运用迭代重定位技术将数据对象在各个簇中重新分配，进而得到最终的相对满意的聚类结果。簇内部数据对象之间差距尽量小，簇之间数据对象差距尽量大才称得上是一个好的聚类分析算法。K-medoids和K-means算法是划分算法中两个比较经典的算法。其他很多划分算法都是从这两个算法演变改进而来的。

2、K-means简介

1957 年 Lloyd首次在文献中提出 k-均值算法，1967 年 MacQueen 在文献中给出了经典的 k-均值算法，描述 k-均值算法的完整理论并进行了详细的研究。 作为最经典的划分聚类算法，k-均值算法的实现并不复杂，具有较高的可伸缩性，同时 k-均值算法具有良好的可靠性和高效性，是一种广泛应用的聚类算法。

3、K-means算法流程

K-means（K均值）算法接受一个参数K用以决定结果中簇的数目。算法开始时，要在数据集中随机选择K个数据对象用来当做k个簇的初始中心，而将剩下的各个数据对象就根据他们和每个聚类簇心的距离选择簇心最近的簇分配到其中。然后重新计算各个聚类簇中的所有数据对象的平均值，并将得到的结果作为新的簇心；逐步重复上述的过程直至目标函数收敛为止。

下面介绍该算法的具体步骤：

1. 对于给定的一组数据，随机初始化K个聚类中心（簇中心）
2. 计算每个数据到簇中心的距离（一般采用欧氏距离），并把该数据归为离它最近的簇。
3. 根据得到的簇，重新计算簇中心。
4. 对步骤2、步骤3进行迭代直至簇中心不再改变或者小于指定阈值。
   K-means算法的流程图

4、K-means伪代码

输入 n 个数据对象集合Xi ;输出 k 个聚类中心 Zj 及K 个聚类数据对象集合 Cj .
Procedure K -means(s , k)
S ={x 1 ,x 2 , …,x n };
m =1;for j =1 to k 初始化聚类中心 Zj ;
do {for i =1 to n
　　for j=1 to k
　　　{D(Xi ,Zj)= Xi -Zj ;if D(Xi ,Zj)=Min{D(Xi ,Zj)}then Xi ∈Cj ;}//归类
　　　if m=1 then Jc(m)=∑kj=1∑ Xi -Zj
2
　　m =m+1;for j =1 to k
　　Zj =(∑
n
i=1 (Xi)
j )/n;//重置聚类中心
　　}while J c (m)-J c (m -1) >ξ

二、K-means代码实现

本文使用的数据集为UCI数据集，分别使用鸢尾花数据集Iris、葡萄酒数据集Wine、小麦种子数据集seeds进行测试，本文从UCI官网上将这三个数据集下载下来，并放入和python文件同一个文件夹内即可。同时由于程序需要，将数据集的列的位置做出了略微改动。数据集具体信息如下表：

数据集	样本数	属性维度	类别个数
Iris	150	4	3
Wine	178	3	3
Seeds	210	7	3

数据集在我主页资源里有，免积分下载，如果无法下载，可以私信我。

1、Python3代码实现

import pandas as pd
import matplotlib.pyplot as plt
from numpy import nonzero
from sklearn.cluster import KMeans
from sklearn.metrics import f1_score, accuracy_score, normalized_mutual_info_score, rand_score
from sklearn.preprocessing import LabelEncoder
from sklearn.decomposition import PCA

df_full = pd.read_csv("iris.csv")  # 鸢尾花数据集 Iris  class=3
# df_full = pd.read_csv("wine.csv")  # 葡萄酒数据集 Wine  class=3
# df_full = pd.read_csv("seeds.csv")  # 小麦种子数据集 seeds  class=3
# df_full = pd.read_csv("wdbc.csv")  # 威斯康星州乳腺癌数据集 Breast Cancer Wisconsin (Diagnostic)  class=2


columns = list(df_full.columns)  # 获取数据集的第一行，第一行通常为特征名，所以先取出
features = columns[:len(columns) - 1]  # 数据集的特征名（去除了最后一列，因为最后一列存放的是标签，不是数据）
df = df_full[features]  # 预处理之后的数据，去除掉了第一行的数据（因为其为特征名，如果数据第一行不是特征名，可跳过这一步）

class_labels = list(df_full[columns[-1]])  # 原始标签
if type(class_labels[0]) != int:
    class_labels = LabelEncoder().fit_transform(df_full[columns[len(columns)-1]])  # 如果标签为文本类型，把文本标签转换为数字标签
    print("此数据集标签为文本类型，已经转化为数字标签！")

K = 3

# 这里已经知道了分3类，其他分类这里的参数需要调试
model = KMeans(n_clusters=K)
# 训练模型
model.fit(df)
# 预测全部数据
label = model.predict(df)
print(label)


def clustering_indicators(labels_true, labels_pred):
    f_measure = f1_score(labels_true, labels_pred, average='macro')  # F值
    accuracy = accuracy_score(labels_true, labels_pred)  # ACC
    normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred)  # NMI
    rand_index = rand_score(labels_true, labels_pred)  # RI
    return f_measure, accuracy, normalized_mutual_information, rand_index


F_measure, ACC, NMI, RI = clustering_indicators(class_labels, label)
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI)
data_reduced = PCA(n_components=2).fit_transform(df)  # 降维

# 打印出聚类散点图
plt.scatter(data_reduced[:, 0], data_reduced[:, 1], marker='o', c='black', s=7)  # 原图
plt.show()
plt.scatter(data_reduced[nonzero(label == 0), 0], data_reduced[nonzero(label == 0), 1], c='red', s=7)
plt.scatter(data_reduced[nonzero(label == 1), 0], data_reduced[nonzero(label == 1), 1], c='blue', s=7)
plt.scatter(data_reduced[nonzero(label == 2), 0], data_reduced[nonzero(label == 2), 1], c='green', s=7)
plt.show()

2、聚类结果分析

本文选择了F值（F-measure，FM）、准确率（Accuracy，ACC）、标准互信息（Normalized Mutual Information，NMI）和兰德指数（Rand Index，RI）作为评估指标，其值域为[0,1]，取值越大说明聚类结果越符合预期。

F值结合了精度（Precision）与召回率（Recall）两种指标，它的值为精度与召回率的调和平均，其计算公式见公式：

$$Precision=\frac{TP}{TP+FP}$$

$$Recall=\frac{TP}{TP+FN}$$

$$F-measure=\frac{2Recall\times Precision}{Recall+Precision}$$

ACC是被正确分类的样本数与数据集总样本数的比值，计算公式如下：

$$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$

其中，TP（True Positive）表示将正类预测为正类数的样本个数，TN （True Negative）表示将负类预测为负类数的样本个数，FP（False Positive）表示将负类预测为正类数误报的样本个数，FN（False Negative）表示将正类预测为负类数的样本个数。

NMI用于量化聚类结果和已知类别标签的匹配程度，相比于ACC，NMI的值不会受到族类标签排列的影响。计算公式如下：

$$NMI=\frac{I\left(U,V\right)}{\sqrt{H\left(U\right)H\left(V\right)}}$$

其中H(U)代表正确分类的熵，H(V)分别代表通过算法得到的结果的熵。

其具体实现代吗如下：

def clustering_indicators(labels_true, labels_pred):
    f_measure = f1_score(labels_true, labels_pred, average='macro')  # F值
    accuracy = accuracy_score(labels_true, labels_pred)  # ACC
    normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred)  # NMI
    rand_index = rand_score(labels_true, labels_pred)  # RI
    return f_measure, accuracy, normalized_mutual_information, rand_index


F_measure, ACC, NMI, RI = clustering_indicators(labels_number, label)
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI)

如果需要计算出聚类分析指标，只要将以上代码插入K-means实现代码中即可。

3、聚类结果

1. 鸢尾花数据集Iris
   

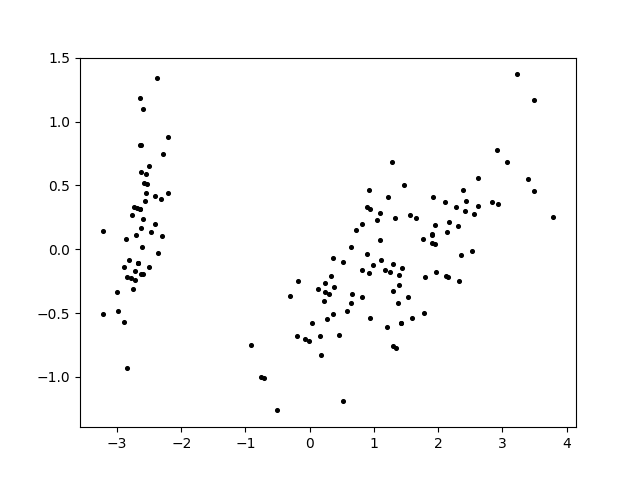
   Iris鸢尾花数据集原图
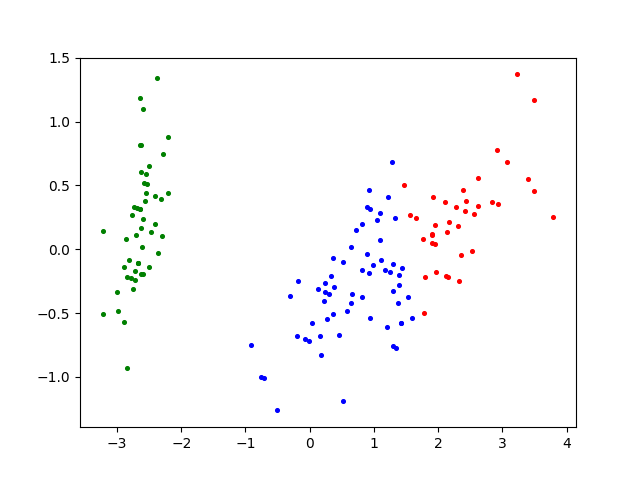
   Iris鸢尾花数据集K-means聚类效果图

2. 葡萄酒数据集Wine
   

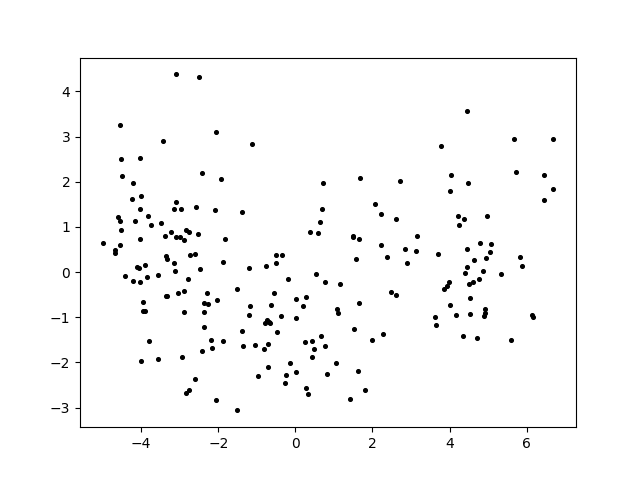
   Wine葡萄酒数据集原图
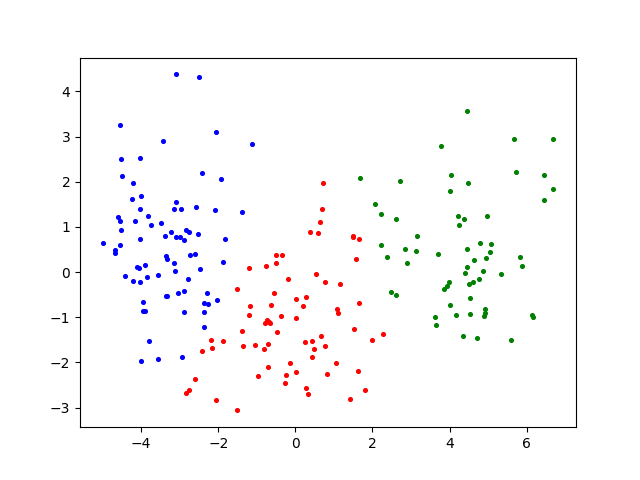
   Wine葡萄酒数据集K-means聚类效果图

3. 小麦种子数据集Seeds
   

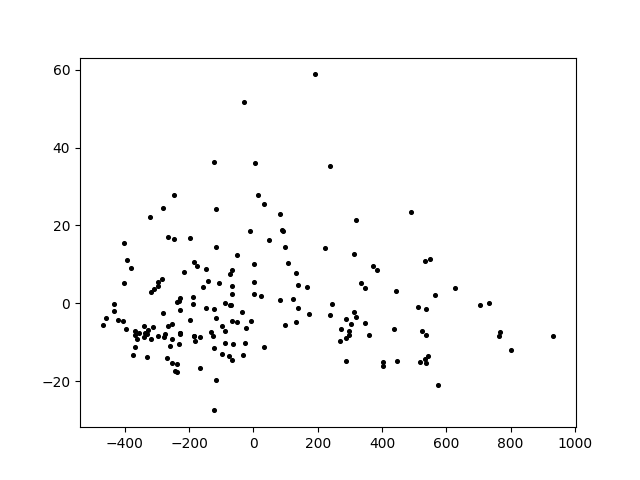
   Seeds小麦种子数据集原图
   Seeds小麦种子数据集K-means聚类效果图

4、K-means算法的不足

K-means算法的核心步骤就是通过不断地迭代，更新聚类簇中心，达到簇内距离最小。算法的时间复杂度很低，因此该算法得到了广泛应用，但是该算法存在着许多不足，主要不足如下：

1. K-means聚类的簇数目需要用户指定。K-means算法首先需要用户指定簇的数目K值，K值的确定直接影响聚类的结果，通常情况下，K值需要用户依据自己的经验和对数据集的理解指定，因此指定的数值未必理想，聚类的结果也就无从保证。
2. K-means算法的初始中心点选取上采用的是随机的方法。K-means算法极为依赖初始中心点的选取：一旦错误地选取了初始中心点，对于后续的聚类过程影响极大，很可能得不到最理想的聚类结果，同时聚类迭代的次数也可能会增加。而随机选取的初始中心点具有很大的不确定性，也直接影响着聚类的效果。
3. K-means采用欧氏距离进行相似性度量，在非凸形数据集中难以达到良好的聚类效果。