文章和代码已经归档至【Github仓库:https://github.com/timerring/algorithms-notes 】或者公众号【AIShareLab】回复 算法笔记 也可获取。
并查集
1.将两个集合合并
2.询问两个元素是否在一个集合当中。
基本原理:每个集合用一棵树来表示。**树根的编号就是整个集合的编号。**每个节点存储它的父节点,p[]表示x的父节点。
- 如何判断树根:if (p[x]== x) //它的父节点就是它自己
- 如何求x的集合编号: while (p[x]!= x)x= p[x];
- 如何合并两个集合:px是x的集合编号,py是y的集合编号。p[x]=y
优化方法
路径压缩(常用),按秩合并。
路径压缩就是将已经找到根节点的所有点,修改其父节点为根节点,以达到降低时间复杂度近似为O(1)的目的。(因为若一直采用循环来找父节点,时间复杂度将会由树的高度决定,十分冗余)。这里是采用递归的方式完成。
注意:通常scanf在读字符串时会自动忽略空格和回车。因此在用scanf读入一个字符或者字母时,推荐采用字符串的形式%S。
例题:合并集合
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
$1≤n,m≤10^5$
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes
code
#include
using namespace std;
const int N = 100010;
int p[N];
int find(int x)
{
// 注意这里是通过 递归 的方式进行查找并且路径压缩的
// 由于返回时逐层返回,因此会把每一层的父节点都置为根节点
if(p[x] != x) p[x] = find(p[x]);
// 返回根节点 即p[x] == x 的节点
return p[x];
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++ )p[i] = i;
while(m --)
{
char op[2];
int a, b;
scanf("%s%d%d", op, &a, &b);
if(*op == 'M') p[find(a)] = find(b);
else
{
if(find(a) == find(b)) puts("Yes");
else puts("No");
}
}
return 0;
} 例题:连通块中点的数量
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a 和 b 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
$1≤n,m≤10^5$
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
code
#include
using namespace std;
const int N = 1e5 + 10;
int p[N], cnt[N];
int find (int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
int n, m;
cin >> n>> m;
for(int i = 1; i <= n; i ++)
{
p[i] = i;
cnt[i] = 1;
}
while(m --)
{
string op;
cin >> op;
int a, b;
if(op == "C")
{
cin >> a >> b;
if(find(a) == find(b)) continue; // 如果同集合 则跳过 避免多次合并
cnt[find(b)] += cnt[find(a)];
p[find(a)] = find(b);
}
if(op == "Q1")
{
cin >> a >> b;
if(find(b) == find(a)) puts("Yes");
else puts("No");
}
if(op == "Q2")
{
cin >> a;
cout << cnt[find(a)] << endl;
}
}
return 0;
} 以上的版本比较便于理解(推荐),也可以采用如下的写法·:
#include
using namespace std;
const int N = 100010;
int n, m;
int p[N], cnt[N];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
{
p[i] = i;
cnt[i] = 1;
}
while(m --)
{
string op;
cin >> op;
int a, b;
if(op == "C")
{
cin >> a >> b;
// 注意这里是先将两个根节点取出来了
a = find(a), b = find(b);
// 避免同一集合中进行合并
if(a != b)
{
// 然后再进行改动
p[a] = b;
cnt[b] += cnt[a];
// 如果不先取出两个根节点保存,而是直接进行操作的话,必须要先进行计数赋值,再改动根节点(即上面两句话颠倒过来,否则会造成原来的根节点发生了变化,存储的cnt也相应改变了)
}
}
else if(op == "Q1")
{
cin >> a >> b;
if(find(a) == find(b)) puts("Yes");
else puts("No");
}
else
{
cin >> a;
cout << cnt[find(a)] << endl;
}
}
return 0;
} 这里需要额外注意的是:a = find(a), b = find(b)先将两个根节点取出来了,如果不先取出两个根节点保存,而是直接进行操作的话,必须要先进行计数赋值,再改动根节点(否则会造成原来的根节点发生了变化,存储的cnt也相应改变了)
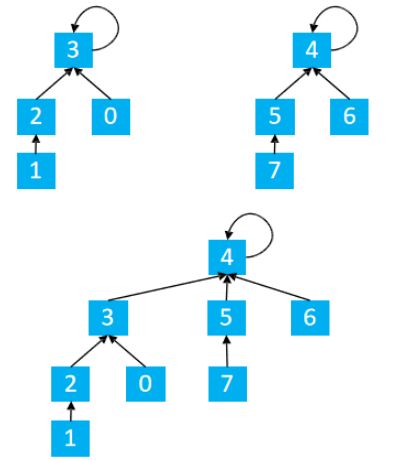
图解分析:
将1,5合并,find(1) = 3 find(5) = 4
p[3] = 4
这时候有8个点相连接,合并的数目更新方式:
- size[3] = 4 以3为根节点下有4个连通块
- size[4] = 4 以4为根节点下有4个连通块
更新4节点的连通块情况 size[4] = size[4] + size[3] = 8
模板总结
int find(int x)
{
// 注意这里是通过递归的方式进行查找并且路径压缩的
// 由于返回时逐层返回,因此会把每一层的父节点都置为根节点
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}例题:食物链
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。
A吃 B,B 吃 C,C 吃 A。
现有 N 个动物,以 1∼N编号。
每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是 2 X Y,表示 X 吃 Y。
此人对 N 个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 X 或 Y 比 N 大,就是假话;
- 当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 N 和 K 句话,输出假话的总数。
输入格式
第一行是两个整数 N 和 K,以一个空格分隔。
以下 K 行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中 D 表示说法的种类。
若 D=1,则表示 X 和 Y 是同类。
若 D=2,则表示 X 吃 Y。
输出格式
只有一个整数,表示假话的数目。
数据范围
$1≤N≤50000$,
$0≤K≤100000$
输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3
基本分析
余1:可以吃根节点
余2:可以被根节点吃
余0:与根节点是同类
因此合并后,x与y同类,则可以说 d[x] + d[px] 与 d[y] 在mod3的意义下是同余的,即可以用以下式子表示
(d[x] + d[px] - d[y]) % 3 = 0 可知 d[px] = d[y] - d[x]
code
#include
using namespace std;
const int N = 50010;
int n, m;
//p[]寻找根节点,d[]求到父节点(find更新前)/ 根节点(find更新后)的距离
int p[N], d[N];
int find(int x)
{
if (p[x] != x)
{
int u = p[x]; // u记录旧的父节点
p[x] = find(p[x]); // 路径压缩,新父节点变成根节点了
d[x] += d[u]; // x到新根节点的距离等于x到旧父节点的距离加上旧父节点到根节点的距离
// 以下版本不好理解:
// 保存根节点
//int t = find(p[x]);
// 更新距离 d[x] = d[x] + d[p[x]]
//d[x] += d[p[x]];
// 指向根节点
//p[x] = t;
}
return p[x];
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) p[i] = i;
int res = 0;
while (m -- )
{
int t, x, y;
scanf("%d%d%d", &t, &x, &y);
// 条件2:当前的话中 X 或 Y 比 N 大,就是假话
if (x > n || y > n) res ++ ;
else
{
// 寻找根节点
int px = find(x), py = find(y);
if (t == 1)
{
// 若在同一个集合 则同类相距距离必是3的倍数 若不是则是假话
// 其中 (d[x] - d[y]) % 3 不可写为 d[x] % 3 != d[y] % 3, 因为 d[x], d[y] 可能为负数(一正一负),可改做 (d[x] % 3 + 3) % 3 != (d[y] % 3 + 3) % 3, 注意:负数 mod 正数为负数
// 相对来说直接写(d[x] - d[y]) % 3还是比较简洁的,因为不为0就是假话
if (px == py && (d[x] - d[y]) % 3) res ++ ;
else if (px != py)
{
// 若不在同一个集合,x 合并到 y 中
p[px] = py;
// 两个距离相减就会变成负数,代码中有d[px] = d[y] - d[x];
d[px] = d[y] - d[x];
}
}
else
{
// 若在同一个集合 则x吃y必满足mod3的意义下d[x]比d[y]大1 可表示为(d[x] - d[y] - 1) mod 3 = 0
if (px == py && (d[x] - d[y] - 1) % 3) res ++ ;
else if (px != py)
{
p[px] = py;
// (d[x] - d[y] - 1) % 3 == 0, d[x] + d[px] - 1 = d[y]
d[px] = d[y] + 1 - d[x];
}
}
}
}
printf("%d\n", res);
return 0;
} ⚠关于公式的详细理解:如果还是难以理解,可以尝试模拟一下过程:
1.初始状态下:
2.普通情况下:
⚠其中关于find的详细理解:
find(x)有两个功能: 1 路径压缩, 2 更新 d[x]
假设有一棵树 a -> b -> c -> d, 根节点为 d。d[b]一开始等于 b、c 之间的距离,再执行完路径压缩命令之后,d[b] 等于b、d之间的距离。 d[a] += d[b]: 为了确保d[a]等于 节点a、d的距离,d[b]必须等于b 、d的距离,所以要先调用find(b)更新d[b], 同时p[x] = find(b)会改变p[x]的值,结果就会变成d[a] += d[d],所以先用一个变量把p[a]的值存起来。
int t = p[x]; // t = p[a] = b
p[x] = find(p[x]); // b = find(b) 每次递归都会对路径进行压缩
d[x] += d[t];// d[a] = d[a](a --> b) + d[b](b --> d)
// find(b):
int t = p[x]; // t = p[b] = c
p[x] = find(p[x]); // c = find(c)
d[x] += d[t];// d[b] = d[b](b --> c) + d[c](c --> d)关键就是既要先执行find(p[x]), 又要让d[x] += d[p[x]]中p[x]的值保持不变,所以代码可以这么写
int t = p[x];
p[x] = find(p[x]);
d[x] += d[t];