灰色预测GM(1,1)Matlab实现

一、介绍：灰色预测是指利用 GM 模型对系统行为特征的发展变化规律进行估计预测。
二、灰色预测的步骤：
1.数据的检验与处理：
首先为了保证使用灰色预测模型的可行性，需要先做级比检验。
$$\begin{gathered} 原始数据为：x^{(0)}=(x^{(0)}(1),x^{(0)}(2),...,x^{(0)}(n)) \\ 数列的级比为：\lambda (k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,...n. \end{gathered}$$
如果所有的级比λ(k)满足以下公式，则数列x(0)可以作为模型进行灰色预测。
$$e^{-\frac{2}{n+1}}<\lambda (k)<e^{\frac{2}{n+1}}$$
若不满足条件，需要进行平移变换：
$$y^{(0)}(k)=x^{(0)}(k)+c,k=1,2,...,n$$
使平移后新数列的级比在条件。

2.建立模型：
建立模型GM(1,1)，则可以得到预测值：
$${\hat{x}}^{(1)}(k+1)=(x^{(0)}(1)-\frac{b}{a})e^{-ak}+\frac{b}{a},k=1,2,...,n-1$$
而且
$${\hat{x}}^{(0)}(k+1)={\hat{x}}^{(1)}(k+1)-{\hat{x}}^{(1)}(k),k=1,2,...,n-1$$

3.检测预测值：
（1）残差检验：令残差为ε(k)，计算：
$$\epsilon (k)=\frac{x^{(0)}(k)-{\hat{x}}^{(0)}(k)}{x^{(0)}(k)},k=1,2,...,n-1$$
如果ε(k)<0.2，则可认为达到一般要求；如果ε(k)<0.1，则认为达到较高要求；
（2）级比偏差值检验：由级比数据λ(k)和发展系数a计算得到：
$$\rho (k)=1-\frac{1-0.5a}{1+0.5a}\lambda (k)$$
如果ρ(k)<0.2，则可认为达到一般要求；如果ρ(k)<0.1，则认为达到较高要求。

Matlab代码：
1.GM1_1函数：

function y = GM1_1(x0,num)
% @brief,GM(1,1)灰色预测模型
% @param,x为待预测的数据
% @param,num为待预测值的数目
% @return,y为[原结果,预测结果]

n = length(x0);
y = zeros(1,n+num);

%% 1.级比检验
% 求级比
lambda = x0(1:n-1)./x0(2:n);

% 级比判断，这里注意需要在后面减去c
minL = exp(-2/(n+1));
maxL = exp(2/(n+1));
c = 0;
while min(lambda) < minL && max(lambda) > maxL
    c = c + 0.1;
    x0 = x0 + c;
    lambda = x0(1:n-1)./x0(2:n);
    if c > 10
        error('无法通过级比检验');
    end
end
%% 2.GM(1,1)建模
% 对原始数据作一次累加
x1 = cumsum(x0);

% 构造数据矩阵B及数据向量Y
alpha = 0.5;
B = [-(alpha*x1(1:end-1)+(1-alpha)*x1(2:end))',ones(n-1,1)];
Y = x0(2:end)';

% 计算u
u = B\Y;
a = u(1);
b = u(2);

% 建立模型
% --------------------方式一：直接解微分方程--------------------
% symbol1 = dsolve('Dx+a*x=b','x(0)=x0');
% symbol1 = subs(symbol1,{'a','b','x0'},{u(1),u(2),x1(1)});
% digits(6),symbol2 = vpa(symbol1);% 为了提高精度，先计算预测值，再显示微分方程的解
% y = subs(symbol2,'t',0:n+num);

% --------------------方式二：采用近似得到的公式--------------------
tmp = b/a;
y(2:n+num) = (x0(1)-tmp).*exp(-a*(1:n+num-1))+tmp;
y(1) = x1(1);

y = [y(1),y(2:end)-y(1:end-1)];
y = y - c;

%% 3.模型检验
% 计算残差
epsilon = (x0 - y(1:n))./x0;
val = max(abs(epsilon));
if val < 0.1
    fprintf("残差检验结果为%.4f，达到较高的要求。\n",val);
elseif val < 0.2
    fprintf("残差检验结果为%.4f，达到一般要求。\n",val);
else 
    fprintf("残差检验结果为%4.f，无法达到要求\n",val);
end

% 级比偏差检验
rho = 1 - (1-0.5*a)/(1+0.5*a)*lambda;
val = max(abs(rho));
if val < 0.1
    fprintf("级比偏差值检验结果为%.4f，达到较高的要求。\n",val);
elseif val < 0.2
    fprintf("级比偏差值检验结果为%.4f，达到一般要求。\n",val);
else 
    fprintf("级比偏差值检验结果为%4.f，无法达到要求\n",val);
end

% 计算百分绝对误差
det = mean(abs(y(2:n)-x0(2:n)));
fprintf("百分绝对误差为%.4f%%\n",det);

% 相对残差Q检验
% 计算相对误差序列
delta = abs(epsilon./x0);
% 计算相对误差Q
Q = mean(delta);
fprintf('相对残差Q检验为%.4f\n',Q);

% 方差比C检验
C = std(epsilon, 1)/std(x0, 1);
fprintf('方差比C检验为%.4f\n',C);

% 小误差概率P检验
S1 = std(x0, 1);
tmp = find(abs(epsilon - mean(epsilon))< 0.6745 * S1);
P = length(tmp)/n;
fprintf('小误差概率P检验为%.4f\n',P);

2.主函数：

clc;
clear;

x0 = [71.1 72.4 72.4 72.1 71.4 72.0 71.6];
n = length(x0);
num = 1;
y = round(GM1_1(x0,1),num);
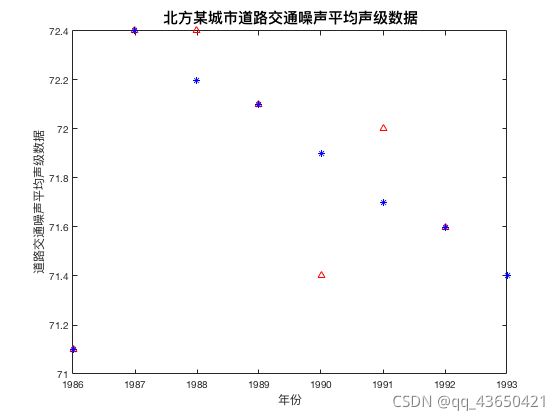
plot(1986:1992,x0,'^r',1986:1993,y,'*b');
xlabel("年份");ylabel("道路交通噪声平均声级数据");
title("北方某城市道路交通噪声平均声级数据");

3.运行结果：