基于阈值的分割方法

一、什么是图像阈值

        在数字图像处理中，阈值是指将图像中的像素值分成两个或更多个不同的区域，通常是为了将图像中的对象从背景中分离出来。阈值分割是一种基本的图像处理技术，它通常用于图像分割、目标检测和特征提取等任务中。阈值的选择是阈值分割的关键。常用的阈值选取方法有：直方图法、最大类间方差法（OTSU法）、基于最大熵的阈值分割法、迭代阈值分割法等等。

二、阈值分割方法

（1）直方图法

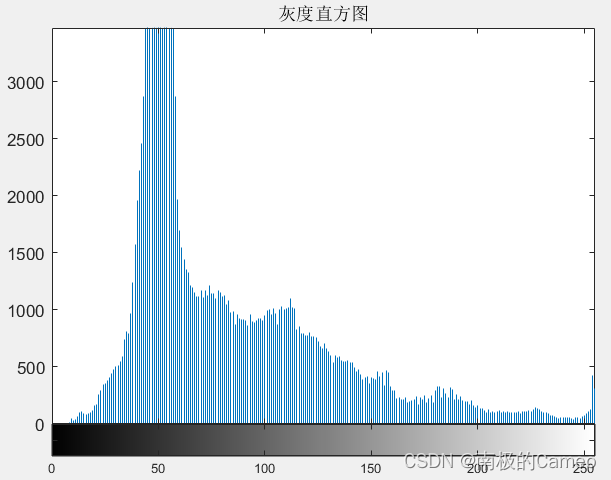
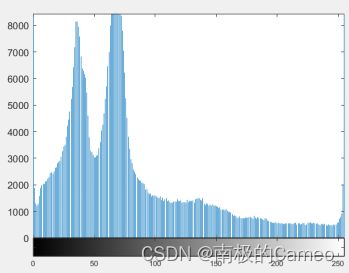
概念：阈值分割直方图法是一种常用的基于图像直方图的阈值选取方法。它利用图像的灰度直方图来确定合适的阈值，从而实现图像的分割。

基于直方图的阈值分割方法，阈值的选择对于分割结果至关重要。通常有以下几种阈值选取方法：

1. 单一阈值：直接选择灰度直方图的峰值位置作为阈值，适用于图像灰度分布单峰情况。这种方法简单直接，但对于灰度分布不均的图像效果不佳。

2. 多阈值：在灰度直方图中选择多个峰值位置作为阈值，适用于图像灰度分布多峰情况。这种方法可以分割出多个目标，但需要手动选择阈值数量和位置。

3. 基于图像统计信息：使用图像的一些统计信息（如平均值、方差等）作为阈值，适用于特定的应用场景。这种方法对于不同场景的图像需要根据具体情况选择适当的统计信息作为阈值

MATLAB代码：

%图像分割（全局阈值，借助直方图）
clc
clear all
I=rgb2gray(imread('peppers.png'));
figure (1)
imhist(I);
title('灰度直方图')
R=I>125;%大于125的地方为白（1），小于为黑（0）
figure(2);
imshow(R);
title('分割图')
figure(3);
imshow(imread('peppers.png'))
title('原始图像')

实验结果：

 在实际应用中，选择阈值通常需要根据图像的特点和应用需求进行调整。这里，由于图像灰度分布不均匀，将中间值作为阈值，分割效果较好。

 （2）最大类间方差法（OTSU法）

OTSU（又称大律法）按照图像的灰度特征，将图像分成背景和前景两部分。方差是灰度分布均匀性的一种度量，背景和前景之间的类间方差越大，说明构成图像的两部分的差别越大。当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。因此，当类间方差最大时分割错分概率小。在MATLAB中， graythresh函数使用最大类间方差法获得图像的阈值。

MATLAB代码：

%Otsu阈值分割
I=rgb2gray(imread('peppers.png'));
M=graythresh(I);%自动获取阈值
J=im2bw(I,M);%根据M的大小来进行分割
subplot(121),imshow(imread('peppers.png'));
title('原始图像')
subplot(122),imshow(J);
title('OTSU阈值分割')

实验结果：

 （3）基于最大熵的阈值分割法

        最大熵阈值分割是一种常用的图像分割方法，通过最大化图像熵来确定图像的阈值，从而将图像分为两个部分：背景和前景。其基本思想是找到一个阈值，将图像分为两个部分，使得两个部分的熵之和最大，即最大化图像的熵。

熵：

        在图像处理中，熵通常用于衡量图像的复杂度，也常被用作图像分割算法中的评价指标。对于一个二维灰度图像，其熵的计算通常分为以下步骤：

1. 统计图像的灰度直方图，即对每个灰度值出现的次数进行计数。通常采用256个灰度级（0~255）进行离散化。

2. 根据灰度直方图计算每个灰度级出现的概率，即将每个灰度值的出现次数除以总像素数。可以得到一个概率分布向量P，其中P[i]表示灰度值为i的像素出现的概率。

3. 使用熵的定义式计算图像的熵，即

   H = - Σ P[i] * log2(P[i])

   其中，Σ是对所有可能的灰度值i求和。

4. 如果需要计算局部熵，则可以将图像划分为若干个小区域，对每个区域计算局部熵。通常将区域大小设置为一个固定值。

在计算熵时，如果像素值分布较为均匀，熵就会比较大，说明图像比较复杂；如果像素值分布较为集中，熵就会比较小，说明图像比较简单。因此，熵可以作为图像复杂度的一种度量方式。同时，熵也可以用于图像分割算法中的阈值选择，通常采用最大熵原理来寻找最佳分割阈值。图像中灰度大于此阈值的像素作为前景，否则作为背景。

MATLAB代码：

clear
Imag = imread('peppers.png');
[X, Y] = size(Imag);
figure ();
imhist(Imag); 
% 计算图像直方图
hist = imhist(Imag);
p = hist/(X*Y); % 各灰度概率
sumP = cumsum(p);
sumQ = 1-sumP;
%将256个灰度作为256个分割阈值，分别计算各阈值下的概率密度函数
c0 = zeros(256,256);
c1 = zeros(256,256);
for i = 1:256
    for j = 1:i
        if sumP(i) > 0
            c0(i,j) = p(j)/sumP(i); %计算各个阈值下的前景概率密度函数
        else
            c0(i,j) = 0;
        end
        for k = i+1:256
            if sumQ(i) > 0;
                c1(i,k) = p(k)/sumQ(i); %计算各个阈值下的背景概率密度函数
            else
                c1(i,k) = 0;
            end
        end
    end 
end
%计算各个阈值下的前景和背景像素的累计熵
H0 = zeros(256,256);
H1 = zeros(256,256);
for i = 1:256
   for j = 1:i
       if c0(i,j) ~=0
           H0(i,j) =  - c0(i,j).*log10(c0(i,j));  %计算各个阈值下的前景熵
       end
         for k = i+1:256
          if c1(i,k) ~=0
              H1(i,k) =  -c1(i,k).*log10(c1(i,k));  %计算各个阈值下的背景熵
          end
       end
   end  
end
HH0 = sum(H0,2);
HH1 = sum(H1,2);
H = HH0 + HH1; 
[value, Threshold] = max(H);
BW = im2bw(Imag, Threshold/255);
figure ();
imshow(BW);
xlabel(['最大熵', num2str(Threshold)]);

 实验结果：

 （4）迭代式阈值分割法

迭代式阈值分割法是一种用于图像分割的方法，它将图像分为背景和前景两个部分。该方法基于灰度值的统计特性，通过迭代的方式自适应地选择一个合适的阈值来将图像分割成两个部分。

迭代式阈值分割法的基本思路如下：

1. 选择一个初始阈值T0和预定义两阈值之差d;
2. 利用阈值T0把给定的图像分割成两组图像，记为R1和R2;
3. 计算R1、R2的均值μ1和μ2;
4. 选择新的阈值T1,T1=(μ1+μ2)/2
5. 重复第2至4步，直到连续两次T的差值小于预设值d为止。

迭代式阈值分割法可以用于处理不同的图像，因为它是自适应的，即它能够根据图像的灰度值分布来选择合适的阈值。此外，该方法也易于实现，并且计算速度较快，因此在实际应用中得到了广泛的应用。

MATLAB代码：

I=imread('peppers.png');
I=im2double(I);
d=0.01;        %预定义两阈值之差
T0=(min(min(I))+max(max(I)))/2; %初始阈值
R1=find(I>T0);  %分组R1
R2=find(I<=T0); %分组R2
m1=mean(I(R1)); %平均灰度值
m2=mean(I(R2));
T1=(m1+m2)/2;   %新阈值
while abs(T1-T0)>d
    T0=T1;
    R1=find(I>T0);
    R2=find(I<=T0);
    T2=(mean(I(R1))+mean(I(R2)))/2;
end
J=im2bw(I,T1);  %把图像转换为二值图，进行阈值分割
set(0,'defaultFigurePosition',[100,100,1000,500]);
set(0,'defaultFigureColor',[1 1 1]);
figure(1);
subplot(121),imshow(I);       
subplot(122),imshow(J);

实验结果：

 三、小结

        基于阈值的分割方法是一种简单且广泛使用的图像分割技术。它基于一个或多个阈值将图像分为不同的区域或对象，通常被用于二值化处理或者灰度级图像的分割。阈值分割方法在实际应用中具有广泛的应用，如图像增强、边缘检测、物体识别等。但是，该方法仅适用于简单的图像分割任务，并且对于噪声和光照变化等影响因素比较敏感。