操作符详解（所有操作符的所有使用方法）

        温馨提示：此文章极具收藏价值，看完后四连养成好习惯（手动滑稽）

目录

操作符的分类

1. 算数操作符

2. 移位操作符

2.1 左移操作符

2.2 右移操作符

3. 位操作符

3.1  ' ^ '

3.2  ' & '

3.3  ' | '

3.4 整合上述操作符

4. 赋值操作符

5. 单目操作符

6. 关系操作符

7. 逻辑操作符

8. 条件操作符

9. 逗号表达式

10. 下标引用、函数调用和结构成员

        10.1 [ ] 下标引用操作符

        10.2 ( ) 函数调用操作符

11. 表达式求值

11.1 隐式类型转换

 11.2 算术转换

11.3 操作符的属性

12. 总结

---

操作符的分类

1. 算数操作符

        +        -        *        /        %

        这里有三点要注意的：

1. 除了 % 操作符之外，其他的几个操作符可以作用于整数和浮点数。
2. 对于 / 操作符如果两个操作数都为整数，执行整数除法。而只要有浮点数执行的就是浮点数除法。（最大类型）
3. % 操作符的两个操作数必须为整数。返回的是整除之后的余数。

---

2. 移位操作符

>>    右移操作符

<<    左移操作符

注意：位移操作符的操作数只能是整数（对其数的二进制进行移位）。

2.1 左移操作符

移位规则

左边抛弃，右边补0

注意：这里实际产生的变化是a×2.

2.2 右移操作符

移位规则

        这里的右移运算要比左移运算复杂一些，分为两种:

1. 逻辑移位
   左边补充0，右边舍弃。
2. 算数移位
   左边补原符号位，右边舍弃。

 注意：不要移动负数，比方说a >> -1 ，这个是标准未定义的~！

移位操作符的用法我会在下面的位操作符中一起讲解~！

---

3. 位操作符

&        按位与（全1则为1，有0为0）

|          按位或（有1则1，全0为0）

^         按位异或（相同为0，不同为1）

注意：它们的操作数为整数。

        为了更好让大家理解，我还是以举例例子的方式进行讲解~

3.1  ' ^ '

        我们在交换两个数的时候，常常用到的方法是不是先创建一个临时变量，将一个变量放到临时变量里，然后把另一个变量放到第一个变量里，最后把第一个存起来的变量再放到另一个变量，如下所示：

	int a = 7;
	int b = 77;
	int c = 0;
    printf("交换前：a=%d b=%d\n", a, b);
	c = a;
	a = b;
	b = a;
    printf("交换后：a=%d b=%d\n", a, b);

        这个很简单，那么如果不让你创建临时变量将两个数交换，你该怎么做呢？

        这时还会有人想到用如下方法：

	int a = 7;
	int b = 77;
	printf("交换前：a=%d b=%d\n", a, b);
	a = a + b;
	b = a - b;
	a = a - b;
	printf("交换后：a=%d b=%d\n", a, b);

        这么仔细一算，诶，好像还真的可以哦，这样不创建临时变量，也实现了两个数之间的交换，但是有没有想过一个问题，因为int形的取值范围是-32768~32767，那么当a+b大于这个范围或者小于这个范围的时候，是不是就出现问题了，有没有更好的办法呢？

        那么接下来就是要用到 ^ 按位异或了，根据我上面给的解释，你肯定能了解了是怎么个运算方式，那么接下来就说它在这道题的用法。

         这样是不是完美的解决了这个问题，当然在实际的写代码中，肯定是要创建一个临时变量更方便而且实用，引出这个只是为了让大家更好的了解 ^ ，原来好多符号不是没有用，只是我们不知道该怎么利用~

3.2  ' & '

        在讲按位与的用法之前，我先给大家说说Google公司的一道笔试题，这个笔试题一出来，其他好多公司分分用这道题来变形，这道题可谓是含金量杠杠的~！

编写代码实现：求一个整数存储在内存中二进制1的个数：

方法一：循环遍历

         分析：用%和/分别对二进制的最低位进行判断，如果a%2 == 1，就说明最低位为1，然后用count++的方式记录并用a/2的方式将这一位删除，循环32次便得出一个数的二进制位中1的个数，下面如图所示。

        当然这个方法是可以求出来正整数的二进制中1的个数，这时你可能会怀疑，诶，为什么要说可以求出来正整数的二进制中1的个数呢，难道负数不能求么？我们继续看~

        这时候你就会发现，诶，为什么是0个啊，-1的补码不是都是1么，不应该是32个1么，但因为-1 % 2应该是等于 -1 的，然后 -1 / 2 = 0 ，所以直接跳出循环，-1的二进制中的个数就为0。

        那么这个方法一定不能用么？答案是否定的，这时如果我们将-1转化为无符号整型，那么就解决了这个问题，因为将-1转化为无符号整型的时候，-1就是一个很大很大的数，因为-1的补码是32个1嘛~

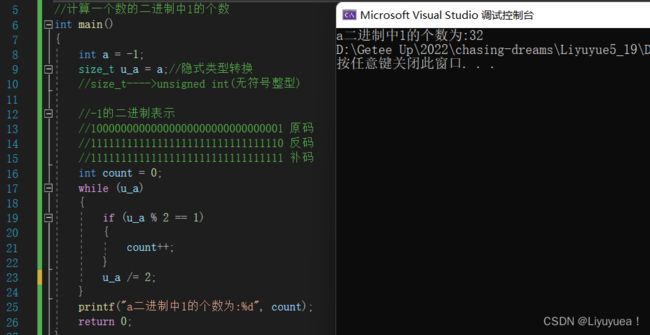
        那么接下来我给大家两个方法，一个是将-1强制类型转换，第二个就是利用隐式类型转换的方式将-1转换为无符号整型（隐式类型转换后面会讲到！）。

        1. 用（）强制类型转换

         2. 用隐式类型转换

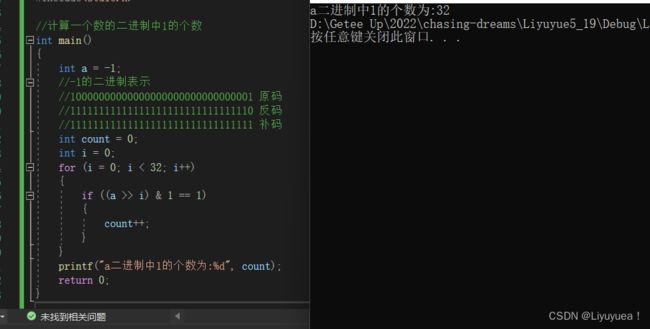
方法二：移位按位与

        分析：因为在运算的时候是按照补码进行的，而且移位操作符不需要考虑正负数的问题，所以让 a 移位1~32位，并分别与1按位与，因为&1的时候只要最低位是1就会得到1，是0就会得到0，当得到1的时候count++就可以得出二进制中有多少个1，接下来我会展示一个正数一个负数形式。

        这样就可以解决正负数的问题，但是要遍历32次，那么还有没有更好的方法呢，那是当然的啦~！我们继续向下看。

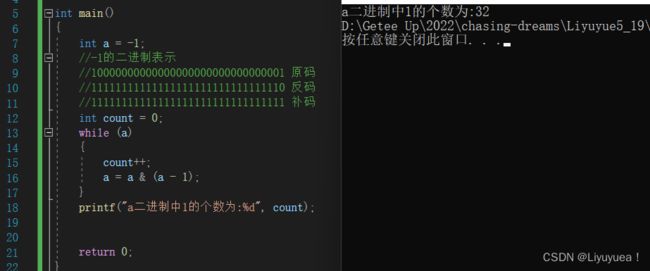
方法三：a & (a - 1 )法

         分析：你们看到这个方法第一时间肯定有点懵吧？不知道什么意思，我来讲解一下，因为 & 的作用是相应位置上如果同为 1 那么就为 1 ，如果有一个为 0 那么就为 0 ，如果让这个数 & 这个数 -1 后，是不是就消掉一个 1 呢，来看下图：

        这只是进行一次，如此往复，每次 a & (a - 1)后count++，当 32 位都为 0 的时候，这个值就为0了，也就数完 a 中有几个 1 了，接下来看代码：

       总结： 讲到这里所有的方法已经讲完了，相信你们也对此处的按位与 & 和上面的移位操作符 << >> 有了更深的认识吧，当然这也不只是一个简单的题，大厂面试的时候很喜欢这个题的！！如果你按照顺序从第一个开始给面试官讲解，面试官肯定对你刮目相看：这小子牛啊，理解的这么深，还知道这么多种方法~！

3.3  ' | '

        这个操作符我目前认为用的很少，有一个作用可以记一下：

        这个运算就是位移 4 位，如果第 4 为 0 的话就会在此数的基础上加，如果有数，此数不变（我也不知道这个算不算作用，如果你们有好的发现，可以在评论区告诉我~！）。

3.4 整合上述操作符

        这里还有一个经典的题，要使用 >> 和 & 也要求对二进制和这俩有深刻的认识~

        编写代码实现：获取一个整数二进制序列中所有偶数位和奇数位，并从高位到地位分别打印出来：

         分析：这里要用到移位 >> 和按位与 & 和前面的用法一样，要明确的是，因为从高位到地位打印二进制位，当打印奇数时要先移位31位，因为你开始没移位的时候就是第1位，移位31位才是第32位，这里很重要！！！，那么偶数位要先移位30位，而且每次递减2位，因为要求单独打印奇数和偶数，接下里我们看代码：

---

4. 赋值操作符

+=

-=

*=

/=

%=

>>=

<<=

&=

|=

^=

注意：都是先操作后赋值。

        （这里的赋值操作符很简单而且容易理解，我就不过多赘述了~！）

---

5. 单目操作符

!                      逻辑反操作（！1 == 0 ；  ！0 == 1）

-                      负值

+                     正值

&                     取地址

sizeof              操作数的类型长度（以字节为单位）

~                     对一个数的二进制按位取反

--                     前置、后置--

++                    前置、后置++

*                       间接访问操作符 (解引用操作符)

(类型)               强制类型转换

        （这里的操作符也没什么可讲解的，理解后直接可以用，下面有一个表格，是对操作符的优先级进行赘述的，到时候再看~！）

---

6. 关系操作符

>

>=

<

<=

!=           （用于测试“不相等”）

==         （ 用于测试“相等”）

注意：在编程的过程中 == 和 = 不小心写错，导致的错误。

        这里我要说一下，千万不要连用关系操作符！千万不要连用关系操作符！！千万不要连用关系操作符！！！

        重要的事情说三遍，我下面来说明原因：

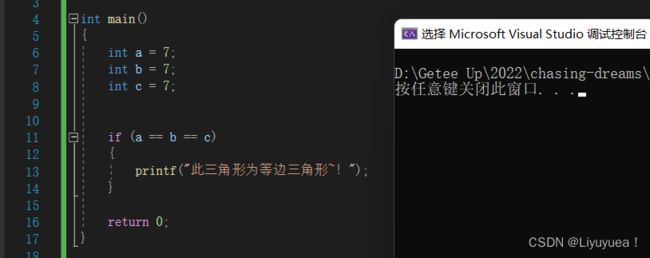
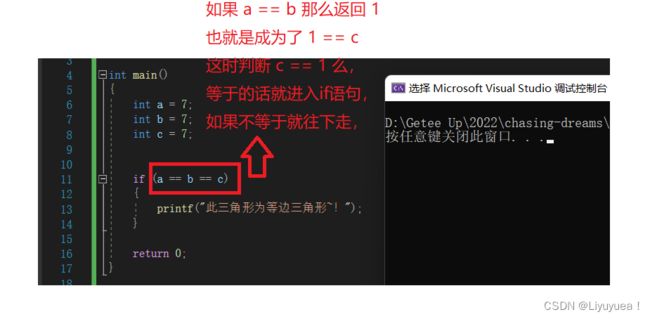
        比如说在比较三角形的三个边的时候，让你写如果 a = b = c 的时候，输出此三角形为等边三角形。

         按理讲这里不应该输入此三角形为等边三角形么，为什么没输入呢？因为这里不可以连等，你要是连等的话是怎么运算的呢，我用过一张图给你讲解：

        这时你应该就懂了，这里的 a == b == c 可不是你想的那样哦，所以千万不要连用关系操作符！，我又说了一遍，如果还出错，那么再回来罚站吧！！！

---

7. 逻辑操作符

&&             逻辑与

||                逻辑或

区分逻辑与和按位与

区分逻辑或和按位或

1&2---·-->0

1&&2---->1

1|2------->3

1||2------>1

        这里有要注意的一点是， && 和 || 是控制求值顺序的，控制求值顺序是什么意思，你可能还不是很懂，接下来我们先看一道题：

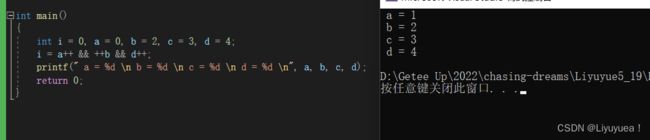
         你们先看看这道题应该输出什么呢，我先多空出几行来，避免不小心看到了~当你想好了，那么看下图：

        看看这里和你想的一样么？

        我想肯定有不少人可能认为 a = 1 , b = 3 , c = 3 , d = 5 .

        但如果你想的就是这个答案，那么恭喜你，你已经会了，但是我还要讲讲为什么会是这样的结果，这里就是因为 && 和 || 是控制求值顺序的，当运算 a++ 的时候，因为 a++ 是后置++，所以 a++ 这时还是 0 ，又因为是 && ，当有一个为 0 的时候就为 0 了，所以它就将后面的 "短路" 了，后面的就不算了，反正都是 0 ，干嘛还要算一遍，这就是&& 和 || 控制求值顺序，相信你们已经明白了，那么如果我们将 a = 1，是不是就不会 "短路" 了呢？

        我们继续看：

         这下就对了吧~！！！这里就正常运行了。

        我们继续来看一个这个题的变形~

         看着眼熟么？对~跟上面那个差不多，只不过这次变为 || 了，现在再看看，你们学会了没~我再给大家空几行，你们好好看看~！

         跟你们想的一样么？我想这次的正确率肯定比上次高~

        这里又是为什么呢，因为 a++ 的时候 a 还是为 0 的，这时是 || 了，它是只要有 1 就没必要算了，有一个 1 就可以了，那么 a++ 的时候 a 还是 0 ，所以不能停呢，这时候 ++b 也运算，它俩运算完就剩下   1 || d++   了，有一个 1 ，那就停下来了，所以 d++ 不运算，所以最后d的值是不变的，而 a + 1 、b + 1 了，这下也懂 || 了吧，下面我直接展示再变形一下的答案，大家看一下就可以了~！ 

        这时就 a++ 了哦，留给你们分析，讲到这里逻辑操作符也讲完喽~ 

注意：这里要分清楚逻辑与、按位与，逻辑或和按位或，不要搞混！

---

8. 条件操作符

exp1 ? exp2 : exp3

        看条件1（exp1）是不是为真，为真输出exp2，为假输出exp3.

---

9. 逗号表达式

exp1, exp2, exp3, …expN

        逗号表达式，就是用逗号隔开的多个表达式。

        逗号表达式，从左向右依次执行。整个表达式的结果是最后一个表达式的结果。

        注意：一定要按要求运算，比如赋值或++ --操作会影响最后表达式结果。

---

10. 下标引用、函数调用和结构成员

        10.1 [ ] 下标引用操作符

操作数：一个数组名 + 一个索引值

int arr[10];    //创建数组

arr[9] = 10;   //实用下标引用操作符。

[ ]的两个操作数是arr和9。

        10.2 ( ) 函数调用操作符

接受一个或者多个操作数：第一个操作数是函数名，剩余的操作数就是传递给函数的参数。

Sum（int a  , int b )

()的两个操作数：Sum和int a , int b 。

---

11. 表达式求值

        表达式求值的顺序一部分是由操作符的优先级和结合性决定。

        同样，有些表达式的操作数在求值的过程中可能需要转换为其他类型。

11.1 隐式类型转换

        C的整型算术运算总是至少以缺省整型类型的精度来进行的。

        为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

整型提升的意义：

        表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度 一般就是int的字节长度，同时也是CPU的通用寄存器的长度。

        因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长 度。

        通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令 中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转 换为int或unsigned int，然后才能送入CPU去执行运算。

//实例1

char a,b,c;

……

a = b + c;

        b和c的值被提升为普通整型，然后再执行加法运算。

        加法运算完成之后，结果将被截断，然后再存储于a中。

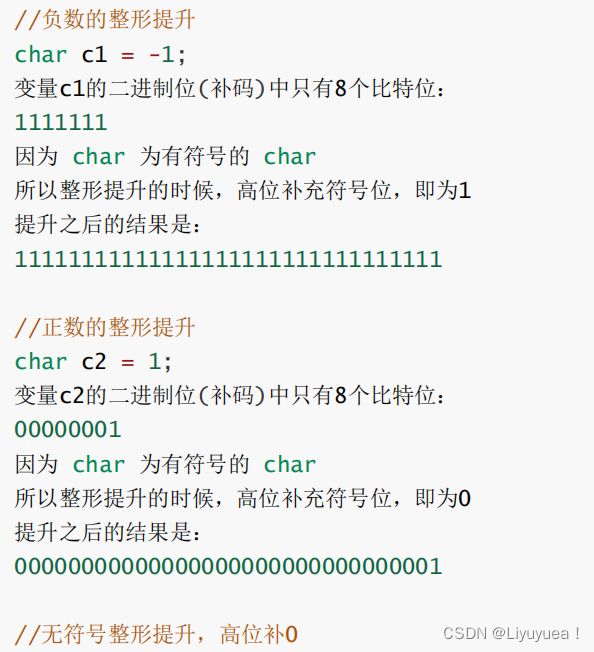
如何进行整体提升呢？

整形提升是按照变量的数据类型的符号位来提升的。

         c只要参与表达式运算,就会发生整形提升,即使是表达式 +c 没有变化,也会发生提升,所以 sizeof(+c) 是4个字节。

         表达式 -c 也会发生整形提升,所以 sizeof(-c) 是4个字节,但是 sizeof(c) ,就是1个字节。

 11.2 算术转换

        如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

        

         注意：转换的时候要注意精度的问题，可能在转换的过程中会丢失精度。

11.3 操作符的属性

        复杂表达式的求值有三个影响的因素。

1. 操作符的优先级
2. 操作符的结合性
3. 是否控制求值顺序。

        两个相邻的操作符先执行哪个？取决于他们的优先级。如果两者的优先级相同，取决于他们的结合性。

        

        操作符优先级。

操作 符	描述	用法示例	结果类型	结合性	是否控制求值顺序
（）	聚组	（表达式）	与表达 式同	N/A	否
（）	函数调用	rexp（rexp，...,rexp）	rexp	L-R	否
[ ]	下标引用	rexp[rexp]	lexp	L-R	否
.	访问结构成员	lexp.member_name	lexp	L-R	否
->	访问结构指针成员	rexp->member_name	lexp	L-R	否
++	后缀自增	lexp ++	rexp	L-R	否
--	后缀自减	lexp--	rexp	L-R	否
!	逻辑反	! rexp	rexp	R-L	否
~	按位取反	~ rexp	rexp	R-L	否
+	单目,表示正值	+ rexp	rexp	R-L	否
-	单目,表示负值	- rexp	rexp	R-L	否
++	前缀自增	++ lexp	rexp	R-L	否
--	前缀自减	-- lexp	rexp	R-L	否
*	间接访问	* rexp	lexp	R-L	否
&	取地址	& lexp	rexp	R-L	否
sizeof	取其长度，以字节表示	sizeof rexp sizeof(类型)	rexp	R-L	否
(类 型）	类型转换	(类型) rexp	rexp	R-L	否
*	乘法	rexp * rexp	rexp	L-R	否
/	除法	rexp / rexp	rexp	L-R	否
%	整数取余	rexp % rexp	rexp	L-R	否
+	加法	rexp + rexp	rexp	L-R	否
-	减法	rexp - rexp	rexp	L-R	否
>>	右移位	rexp >> rexp	rexp	L-R	否
<<	左移位	rexp << rexp	rexp	L-R	否
>	大于	rexp > rexp	rexp	L-R	否
>=	大于等于	rexp >= rexp	rexp	L-R	否
<	小于	rexp < rexp	rexp	L-R	否
<=	小于等于	rexp <= rexp	rexp	L-R	否
==	等于	rexp == rexp	rexp	L-R	否
!=	不等于	rexp != rexp	rexp	L-R	否
&	位与	rexp & rexp	rexp	L-R	否
^	位异或	rexp ^ rexp	rexp	L-R	否
|	位或	rexp | rexp	rexp	L-R	否
&&	逻辑与	rexp&& rexp	rexp	L-R	是
||	逻辑或	rexp || rexp	rexp	L-R	是
? :	条件操作符	rexp ? rexp : rexp	rexp	N/A	是
=	赋值	lexp = rexp	rexp	R-L	否
+=	以...加	lexp += rexp	rexp	R-L	否
-=	以...减	lexp -= rexp	rexp	R-L	否
*=	以...乘	lexp *= rexp	rexp	R-L	否
/=	以...除	lexp /= rexp	rexp	R-L	否
%=	以...取模	lexp %= rexp	rexp	R-L	否
>=	以...右移	lexp >>= rexp	rexp	R-L	否
&=	以...与	lexp &= rexp	rexp	R-L	否
^=	以...异或	lexp ^= rexp	rexp	R-L	否
|=	以...或	lexp |= rexp	rexp	R-L	否
，	逗号	rexp，rexp	rexp	L-R	是

        lexp表示左值表达式，rexp表示右值表达式。

        记住：左值意味着一个位置，而右值意味着一个值。所以，在使用右值的地方也可以使用左值，但在需要左值的地方不能使用右值。

        （左值和右值通俗的讲，左值就是能够出现在赋值符号左面的东西，而右值就是那些可以出现在赋值符号右面的东西。）

        L-R是从左到右，R-L是从右到左，N/A是无结合性。

        图表又上到下优先级降低~

一些问题表达式

         接来下我会写出问题表达式并加以分析。

         所以我们在写代码的时候要避免这种情况发生，不要写出有歧义的代码，接下来我再给大家写一个奇怪的代码，让大家解读并感受一下~！

12. 总结

        当我们懂得了它们的优先级和结合性，那么我们就可以算出一个式子的值，而且这个值是唯一解么？肯定不是，即使你懂得了它们的优先级和结合性，当你写出有歧义的式子，不同的编译器也会产生不同的答案，你这么写有点太为难编译器了~所以要想不出错，首先你要写的好！虽然说大佬都是20%的时间在写代码80%的时间在改代码，但是！！！写出来连编译器都不知道怎么办的式子，你怎么改呢！！！

         博主创作不易，花费了好多好多时间，把零碎的知识整合到一起，然后扣细节的讲出来，这个文章绝对有收藏价值，麻烦大哥大姐们给博主点赞加评论加收藏吧！！

        也可以关注博主，我会更新更优质的内容供大家学习，大家一起进步！！！

        你们的四连就是我创作的动力~蟹蟹！！！