深度学习笔记之Transformer(一)注意力机制基本介绍

引言

从本节开始，将介绍$\text{Transformer}$模型。本节将介绍注意力机制的基本逻辑。

回顾：$\text{Seq2seq}$模型中的注意力机制

关于注意力机制$(\text{Attention})$，我们并不陌生。在基于循环神经网络的模型结构——$\text{Seq2seq}$中介绍了一种注意力机制。

该注意力机制的动机在于：从编码器$(\text{Encoder})$中产生的$\text{Context}$向量$\mathcal{C}$可能存在梯度消失问题，从而使解码器中生成出的序列信息与编码过程中的初始时刻序列信息关联不大，也就是对齐问题。

而注意力机制在$\text{Seq2seq}$结构中的使用逻辑是：使用注意力机制对解码过程中的每一时刻$t=1,2,\cdots ,{\mathcal{T}}^{\prime }$都使用专属于该时刻的$\text{Context}$向量${\mathcal{C}}_t$来替代原始所有时刻共用的$\text{Context}$向量$\mathcal{C}$。关于${\mathcal{C}}_t$的表示如下：

• 已知解码器$(\text{Decoder})$关于$t$时刻的序列信息$h_{\mathcal{D}}^{(t)}$以及对应编码器$(\text{Encoder})$中所有时刻的序列信息$\left[h_{\mathcal{L};j};h_{\mathcal{R};(\mathcal{T}+1-j)}\right](j=1,2,\cdots ,\mathcal{T})$，构建神经网络对每对序列信息之间的关联关系进行评估：
  • 每对序列具体是指$h_{\mathcal{D}}^{(t)}$与每一个$\left[h_{\mathcal{L};j};h_{\mathcal{R};(\mathcal{T}+1-j)}\right]$配对并进行评估。
  • 配对的具体操作是将其拼接$(\text{Concatenate})$后作为线性计算层$\text{Attn}$的输入,并得到输出结果${\mathcal{O}}_{tj}(j=1,2,\cdots ,\mathcal{T})$
    $$\{\begin{array}{l}\begin{array}{rl}{\mathcal{O}}_t& ={\left({\mathcal{O}}_{t1},{\mathcal{O}}_{t2},\cdots ,{\mathcal{O}}_{t\mathcal{T}}\right)}^T\\ {\mathcal{O}}_{tj}& =\text{Attn}\left(h_{\mathcal{D}}^{(t)},\left[h_{\mathcal{L};j};h_{\mathcal{R};(\mathcal{T}+1-j)}\right]\right)\\ & ={\mathcal{W}}_{\text{Attn}}\cdot \left\{\text{Concat}\left[h_{\mathcal{D}}^{(t)},\left[h_{\mathcal{L};j};h_{\mathcal{R};(\mathcal{T}+1-j)}\right]\right]\right\}+b_{\text{Attn}}\end{array}\end{array}$$
• 对线性计算层输出${\mathcal{O}}_t$使用$\text{Tanh}$激活函数进行映射；
  $${\mathcal{O}}_t=\text{Tanh}({\mathcal{O}}_t)$$
• 构建神经网络层将${\mathcal{O}}_t$中的每一个分量映射成标量信息，该信息的物理意义是：$h_{\mathcal{D}}^{(t)}$与所有编码器输出$\left[h_{\mathcal{L};j};h_{\mathcal{R};(\mathcal{T}+1-j)}\right](j=1,2,\cdots ,\mathcal{T})$的评估分数。最后使用激活函数$\text{Softmax}$，将该分数映射成比重结果：
  $$\begin{array}{rl}{\mathcal{E}}_t& ={\mathcal{V}}^T{\mathcal{O}}_t\\ & \Rightarrow (e_{t1},e_{t2},\cdots ,e_{t\mathcal{T}}{)}^T\\ s_{tj}& =\text{Softmax}(e_{tj})\\ & =\frac{\exp (e_{tj})}{{\sum }_{k=1}^{\mathcal{T}}\exp (e_{tk})}\\ {\mathcal{S}}_t& =(s_{t1},s_{t2},\cdots ,s_{t\mathcal{T}})\end{array}$$
• 在得到$\text{Softmax}$结果${\mathcal{S}}_t$后，对${\mathcal{H}}_{Bi}=\left[\left(h_{\mathcal{L};1};h_{\mathcal{R};\mathcal{T}}\right),\left(h_{\mathcal{L};2};h_{\mathcal{R};\mathcal{T}-1}\right),\cdots ,\left(h_{\mathcal{L};\mathcal{T}};h_{\mathcal{R};1}\right)\right]$进行线性计算。即：${\mathcal{S}}_t$中的每一个分量与${\mathcal{H}}_{Bi}$对应结合，得到${\mathcal{C}}_t$。
  $${\mathcal{C}}_t={\mathcal{S}}_t\ast {\mathcal{H}}_{Bi}$$

注意力机制的简单描述

从心理学的角度观察，人类通常从刻意$(\text{Volitional})$信息与无意$(\text{Nonvolitional})$信息中选择注意点并进行获取。

• 刻意信息是指：自我主观想要获取的信息。例如：一张人脸图片中，我想要观察这个人的瞳孔颜色，而不是这个人的发量、性别等其他信息。

  就像上面$\text{Seq2seq}$注意力机制的例子，我们想要主观地认知$h_{\mathcal{D}}^{(t)}$与编码器各时刻输出$\left[h_{\mathcal{L};j};h_{\mathcal{R};(\mathcal{T}+1-j)}\right]$之间的关联关系，而不仅仅是编码器产生的序列信息$\mathcal{C}$。

• 而无意信息是指：相比于刻意信息，我们不经意间获取的信息。例如如下散点图：
  
  很明显，我们注意到：这张图片中有一个红色的点。这并不是我们主观发现的，而是红色点区别于其他点的颜色性质使我们注意到了它。

很明显，刻意和无意信息在逻辑顺序上存在区别：

• 刻意：主动注意事物某一种属性 $\Rightarrow$ 得到注意信息；
• 无意：事物原有的特点比较突出 $\Rightarrow$ 从而该事物被注意到。

在深度学习中的一些操作仅考虑无意信息。例如：

• 卷积操作：它可能描述的是时间中其他过去时刻对该时刻的累积影响；或者是空间中，某图片周围像素点信息对中间像素点信息的累积影响。
• 全连接神经网络：对输入分布进行线性运算和非线性映射，将输入信息转化为抽象特征。
• 池化操作，如最大池化层$(\text{MaxPooling})$。该操作的思路在于：用一个值描述当前窗口信息的综合情况。

上述操作仅考虑无意信息的逻辑在于：它们对所有输入信息均一视同仁。也就是说，上述操作所得到的信息均归结于数据自身信息的性质。如：图像的边缘、明亮鲜艳的颜色等等。但这些信息并不是我们主观意识得到的信息。

相反，$\text{Seq2seq}$注意力机制中存在我们的主观意识，即刻意信息：在机器翻译任务中，刻意信息是指：某时刻的翻译结果与被翻译的句子中的某些词存在关联关系。

这里依然使用$\text{Seq2seq}$注意力机制动机中的例子：
我 是 一名 演员 。$\iff \text{I am an actor .}$

关于$t=3$时刻翻译结果$\text{ an }$与原句之间存在如下关联关系：
其中原句中的‘一名’在英文中描述一个‘不定冠词’，但不定冠词中表示‘一个’的不定冠词有两种：$\text{a,an}$,但为什么选择$\text{an}$而不是$\text{a}$是因为‘演员’$\text{actor}$开头是元音字母。因此，‘一名、演员’这两个词都对翻译结果$\text{an}$产生了影响。

在深度学习中，刻意信息被称作查询向量$(\text{Query})$；而环境信息(数据自身的信息)被描述成无意信息$(\text{Key})$与值$(\text{Value})$组成的键值对。

• 其中$\text{Key}$和$\text{Value}$可以是完全相同，完全相同意味着：主观意识没有对无意信息进行干预。
• 当然，$\text{Key}$和$\text{Value}$也可以是不同的，不同的$\text{Key,Value}$意味着：该无意信息根据主观意识进行描述产生的$\text{Value}$，而不是无意信息自身。

而注意力机制，也称作注意力池化层$(\text{Attention Pooling})$。它的作用在于：基于查询向量$\text{Query}$，从环境信息中有注意力偏向地选择出若干个键值对$(\text{Key-Value Pairs})$作为输出。其余的信息则不会输出出去。

注意力机制的机器学习范例：$\text{Nadaraya-Watson}$核回归

深度学习中的注意力机制确实是近$10$年内的产物，但注意力机制自身并不是。早在$60$年代提出一种非参数注意力的池化层——$\text{Nadaraya-Watson}$核回归。

给定数据$\mathcal{D}=\{(x^{(i)},y^{(i)}){\}}_{i=1}^N$，对该数据做回归任务。它对应函数公式表示如下：
$$y^{(i)}=2\times \sin (x^{(i)})+[x^{(i)}{]}^{0.8}+ϵ$$
其中$2\times \sin (x^{(i)})+[x^{(i)}{]}^{0.8}$表示真实分布${\mathcal{P}}_{data}$的函数，$ϵ\sim \mathcal{N}(0,0.5)$表示噪声信息。

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)

def f(x):
    return 2 * np.sin(x) + x ** 0.8

SampleNum = 50
StandardX = np.linspace(0,5,200)
StandardY = [f(i) for i in StandardX]

TrainX = [np.random.uniform(0,5) for _ in range(SampleNum)]
TrainY = [f(j) + np.random.normal(0.0,0.5) for j in TrainX]

plt.plot(StandardX,StandardY,c="tab:blue")
plt.scatter(TrainX,TrainY,c="tab:orange")
plt.show()

对应训练数据(橙色点)以及真实函数(蓝色线)表示如下：

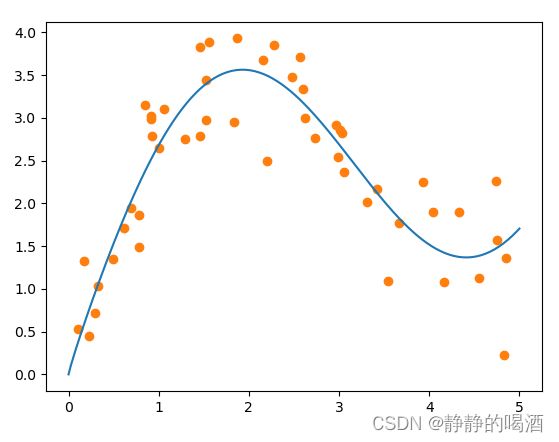
如果使用最简单的平均池化操作对标签进行预测。即：将所有训练数据对应标签取平均值。
$$f(x)=\frac{1}{N}\sum _{i=1}^N{y}^{(i)}$$
基于该预测结果对应的函数图像表示如下(紫色虚线)：

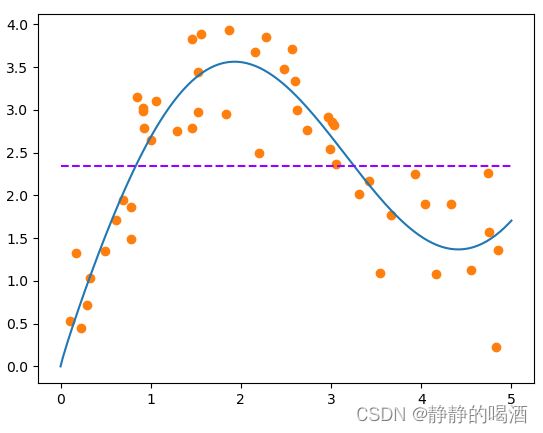
很明显，这就是一个极端欠拟合$(\text{Under-Fitting})$现象。也就是说：无论输入什么数据，预测结果均是该值。重新观察平均池化操作，我们发现：它对训练集内任意标签的权重(关注程度)均相同，为$\begin{array}{r}\frac{1}{N}\end{array}$;

而$\text{Nadaraya-Watson}$核回归描述了一种无参数注意力池化的思路：为训练集内不同样本的标签赋予不同的权重。
$$f(x)=\sum _{i=1}^N\frac{\kappa (x,x^{(i)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(i)}$$
其中，$\kappa (x,x^{(i)})$表示关于随机变量$x$的核函数。在之前介绍过$\kappa (x,x^{(i)})$描述的是：向量$x$与$x^{(i)}$被映射到高维空间后的内积结果：
$$\kappa (x,x^{(i)})=[\varphi (x){]}^T\cdot \varphi (x^{(i)})$$
而内积大小描述的是余弦相似度。这意味着：核函数的结果描述样本之间的相似性。

回顾上式，将$f(x)$展开：
$$\begin{array}{rl}f(x)& =\frac{\kappa (x,x^{(1)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(1)}+\frac{\kappa (x,x^{(2)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(2)}+\cdots +\frac{\kappa (x,x^{(N)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(N)}\end{array}$$
可以看出：所有关于$y^{(i)}(i=1,2,\cdots ,N)$的系数，分母是相同的。那么这意味着：核函数的大小决定对应系数的大小。而系数的大小决定与对应向量$y^{(i)}$注意力偏向的大小。

这里使用高斯核函数，也就是径向基核函数($\text{Radial Basis Function,RBF}$)为例：
$$\kappa (x,x^{(j)})=\exp \left\{-\frac{1}{2{\sigma }^2}||x-x^{(j)}|{|}^2\right\}$$
其中$||x-x^{(j)}|{|}^2$描述样本$x$与样本$x^{(j)}$之间的关联关系。以$||x-x^{(j)}|{|}^2$作为自变量，观察$\kappa (x,x^{(j)})$与自变量之间的关系：

import math
import numpy as np
import matplotlib.pyplot as plt

def RBF(x,sigma):
    return math.exp(-1 * (1 / (2 * (sigma ** 2))) * x)

x = list(np.linspace(0,10,200))
y = [RBF(i,sigma=0.5) for i in x]
plt.plot(x,y)
plt.show()

返回结果表示如下：

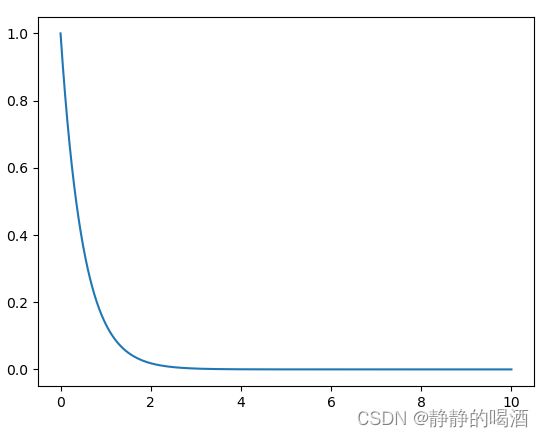
很明显可以看出：以径向基核函数为前提的条件下，样本$x$与某训练数据$x^{(j)}$之间越接近(两者之间的差距越小,$||x-x^{(j)}|{|}^2\to 0$)，核函数结果越大，从而$\text{Nadaraya-Watson}$核回归中，关于$y^{(i)}$的系数越大。因此，$\text{Nadaraya-Watson}$核回归依然在求均值，只不过这次均值的权重包含了对各训练样本关联程度的注意力偏向。

从公式推导的角度也能看到其中的效果。将径向基核函数带入到上式中：
很明显，中间的系数项就是$\text{Softmax}$函数的表达式。
$$\begin{array}{rl}f(x)& =\sum _{i=1}^N\frac{\kappa (x,x^{(i)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(i)}\\ & =\sum _{i=1}^N\frac{\exp \left\{-\frac{1}{2{\sigma }^2}||x-x^{(i)}|{|}^2\right\}}{{\sum }_{j=1}^N\exp \left\{-\frac{1}{2{\sigma }^2}||x-x^{(j)}|{|}^2\right\}}\cdot y^{(i)}\\ & =\sum _{i=1}^N\text{Softmax}\left[-\frac{1}{2{\sigma }^2}||x-x^{(i)}|{|}^2\right]\cdot y^{(i)}\end{array}$$

根据$\text{Softmax}$函数的性质，上述操作相当于：将训练数据中的每个样本各自视作一个类别，$\text{Softmax}$结果相当于陌生样本对每个类别所归属的概率信息。并将该概率信息作为权重，执行带权重的均值计算。基于此，我们能够想到两种极端情况：

• 陌生样本$x$与训练数据中的某样本$x^{(j)}(j\in \{1,2,\cdots ,N\})$重合。这意味着：$\text{Softmax}$函数的所有权重全部集中在$y^{(j)}$上面。因而该样本$x$的预测结果就是$y^{(j)}$；
• 陌生样本$x$与所有训练数据$x^{(j)}(j=1,2,\cdots ,N)$都足够远(假设是无穷大)，这导致$x$关于所有$x^{(j)}$的$\text{Softmax}$系数均相同。从而该模型的预测结果就是平均值自身：
  • $\text{Softmax}$系数结果相同$\to$既然核函数结果都是‘无限趋近与’$0$的值，它们之间的差别自然无关紧要。
  • 取平均值可以理解为$\text{Nadaraya-Watson}$核回归最坏的预测情况。
    $$f(x)=\frac{1}{N}\sum _{i=1}^N{y}^{(i)}$$

从代码的角度描述$\text{Nadaraya-Watson}$核回归的效果：
文章末尾附完整代码。

def NWKernelRegression(StandardX,TrainX,TrainY,Sigma):

    def RBF(x,xSample,Sigma):
        return math.exp(-1 * (1 / (2 * (Sigma ** 2))) * ((x - xSample) ** 2))

    def SoftmaxFunction(x,xSample,Sigma):
        return RBF(x,xSample,Sigma) / sum([RBF(x,i,Sigma) for i in TrainX])

    def NWKernelResult(x,Sigma):
        KernelResultList = list()
        for _,(xSample,ySample) in enumerate(zip(TrainX,TrainY)):
            SoftmaxCoeff = SoftmaxFunction(x,xSample,Sigma)
            KernelResultList.append(SoftmaxCoeff * ySample)

        return sum(KernelResultList)

    return [NWKernelResult(j,Sigma) for j in StandardX]

当超参数——高斯核函数的$\sigma =0.5$时，回归结果表示如下(绿色线)：

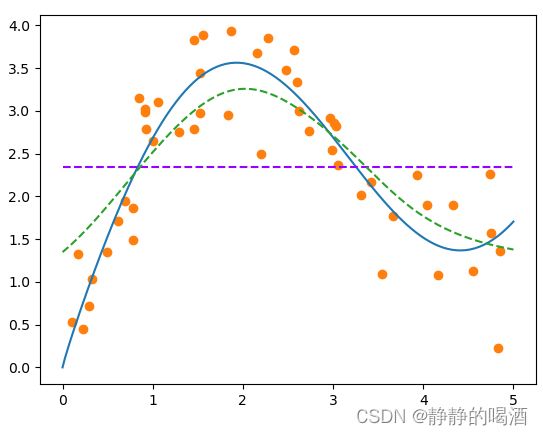
当然，也可以继续调节$\sigma$，找到一个更优秀的拟合效果甚至是过拟合效果：

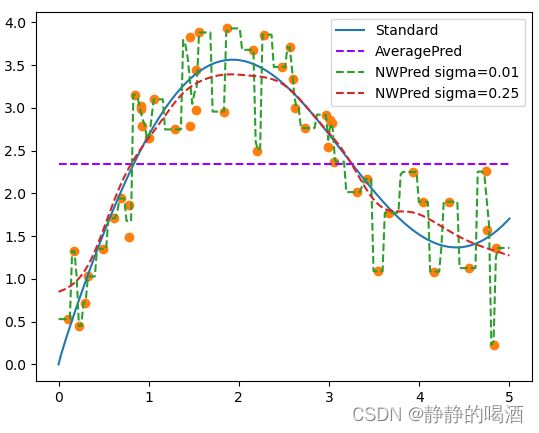
可以发现：我们直接将陌生数据喂给训练集即可，没有显式的训练过程。这种处理方式被称作懒惰学习$(\text{Lazy Learning})$。之前介绍的另一种懒惰学习的代表——$\mathcal{K}$近邻学习算法

$\text{Nadaraya-Watson}$核回归与注意力机制的关联

根据注意力机制的思路，可以将训练数据$\mathcal{D}=\{x^{(i)},y^{(i)}{\}}_{i=1}^N$中，每个特征信息$x^{(i)}(i=1,2,\cdots ,N)$看做是无意信息$\text{Key}$，而对应的$y^{(i)}$则表示每个键值对$\text{Key}$对应的$\text{Value}$信息。

而每一个陌生样本$x$被视作$\text{Query}$，原因是：我们想要主观获取$\text{Query}$与各个$\text{Key}$之间的关联关系。这个关联关系的分布就是$\text{Softmax}$构成的序列向量：
$$\mathcal{G}\left[\text{Query}(x),\text{Key}(x^{(1)},x^{(2)},\cdots ,x^{(N)})\right]={\left[\frac{\kappa (x,x^{(1)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})},\frac{\kappa (x,x^{(2)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})},\cdots ,\frac{\kappa (x,x^{(N)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\right]}_{N\times 1}^T$$
最终将注意力分布$\mathcal{G}$与各个$\text{Key}$对应的$\text{Value}$相结合，得到注意力结果：
f ( x ) = { G [ Query ( x ) , Key ( x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) ) ] } T ⋅ Value ( y ( 1 ) , y ( 2 ) , ⋯   , y ( N ) ) = [ κ ( x , x ( 1 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , κ ( x , x ( 2 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , ⋯   , κ ( x , x ( N ) ) ∑ j = 1 N κ ( x , x ( j ) ) ] 1 × N ( y ( 1 ) y ( 2 ) ⋮ y ( N ) ) N × 1 = ∑ i = 1 N κ ( x , x ( i ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( i ) \begin{aligned} f(x) & = \left\{\mathcal G \left[\text{Query}(x),\text{Key}(x^{(1)},x^{(2)},\cdots,x^{(N)})\right]\right\}^T \cdot \text{Value}(y^{(1)},y^{(2)},\cdots,y^{(N)}) \\ & = \left[\frac{\kappa(x,x^{(1)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\frac{\kappa(x,x^{(2)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\cdots,\frac{\kappa(x,x^{(N)})}{\sum_{j=1}^N \kappa(x,x^{(j)})}\right]_{1 \times N} \begin{pmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(N)} \end{pmatrix}_{N \times 1} \\ & = \sum_{i=1}^N \frac{\kappa(x,x^{(i)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(i)} \end{aligned} f(x)​={G[Query(x),Key(x(1),x(2),⋯,x(N))]}T⋅Value(y(1),y(2),⋯,y(N))=[∑j=1N​κ(x,x(j))κ(x,x(1))​,∑j=1N​κ(x,x(j))κ(x,x(2))​,⋯,∑j=1N​κ(x,x(j))κ(x,x(N))​]1×N​ ​y(1)y(2)⋮y(N)​ ​N×1​=i=1∑N​∑j=1N​κ(x,x(j))κ(x,x(i))​⋅y(i)​

附：$\text{Nadaraya-Watson}$核回归示例完整代码

import numpy as np
import math
import matplotlib.pyplot as plt
np.random.seed(42)


def f(x):
    return 2 * np.sin(x) + x ** 0.8

def Average(TrainY):
    return [float(np.mean(TrainY)) for _ in range(200)]

def NWKernelRegression(StandardX,TrainX,TrainY,Sigma):

    def RBF(x,xSample,Sigma):
        return math.exp(-1 * (1 / (2 * (Sigma ** 2))) * ((x - xSample) ** 2))

    def SoftmaxFunction(x,xSample,Sigma):
        return RBF(x,xSample,Sigma) / sum([RBF(x,i,Sigma) for i in TrainX])

    def NWKernelResult(x,Sigma):
        KernelResultList = list()
        for _,(xSample,ySample) in enumerate(zip(TrainX,TrainY)):
            SoftmaxCoeff = SoftmaxFunction(x,xSample,Sigma)
            KernelResultList.append(SoftmaxCoeff * ySample)

        return sum(KernelResultList)
    return [NWKernelResult(j,Sigma) for j in StandardX]

SampleNum = 50
StandardX = np.linspace(0,5,200)
StandardY = [f(i) for i in StandardX]

TrainX = [np.random.uniform(0,5) for _ in range(SampleNum)]
TrainY = [f(j) + np.random.normal(0.0,0.5) for j in TrainX]
AveragePred = Average(TrainY)
NWKernelPred1 = NWKernelRegression(StandardX,TrainX,TrainY,Sigma=0.01)
NWKernelPred2 = NWKernelRegression(StandardX,TrainX,TrainY,Sigma=0.25)

plt.plot(StandardX,StandardY,c="tab:blue",label="Standard")
plt.plot(StandardX,AveragePred,c="#9900ff",linestyle="--",label="AveragePred")
plt.plot(StandardX,NWKernelPred1,c="tab:green",linestyle="--",label="NWPred sigma=0.01")
plt.plot(StandardX,NWKernelPred2,c="tab:red",linestyle="--",label="NWPred sigma=0.25")
plt.scatter(TrainX,TrainY,c="tab:orange")
plt.legend(loc=0)
plt.show()

相关参考：
64 注意力机制【动手学深度学习v2】
注意力汇聚：Nadaraya-Watson 核回归