排序算法——参考《王道考研》+《大话数据结构》
一、简述
昨天面试写一个笔试题,题目是:列举几种排序算法并指出它的时间复杂度。 鸭儿哟,我居然忘地差不多了,所以今天特地来总结一波。话不多说:直接low它。
二、排序框架
基本概念和外部排序,我们“从长计议”,今天我们直接low内部排序。我们将以一个A[n]数组为例排序此数组,当然这里需要回顾C语言的一个知识点:为什么传递数组形参,需要指定其长度? 答:当数组做参数时候,不论是:int a[] int *a 都只是传递一个指针,它指向的是已经在其他地方分配好的内存空间。形参只是一个指针,它指向的是已经在其他地方分配好的内存空间,即:指向数组的第一个元素,并无法知道这个数组有多长,所以需要显式的参数传递给函数。
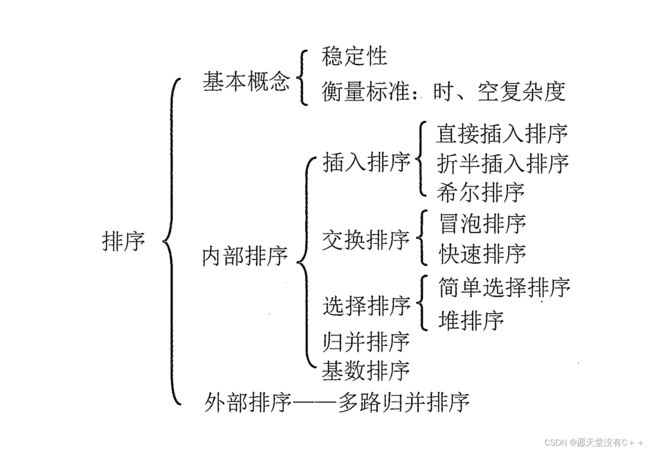
三、插入排序(直接插入、折半插入、希尔)
中心思想: 每次将一个待排序的记录L(i)按照关键字大小插入前面已排好的子序列L[1...i-1],直到全部记录插入完成。
备注: 为什么我们要从L[1]位置而不是L[0]开始排序呢?目的:设置一个哨兵 在移动的过程中,可以作为 “临时缓冲区” 来放置可能会被操作的元素,具体如何使用,我们后续有具体介绍。
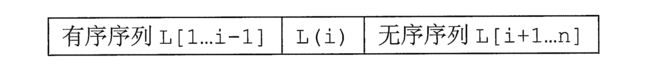
1、直接插入排序
步骤:
1) 查找出L(i)在L[1..i-1]的插入位置k。
2) 将L[k-1]中的所有元素依次后移一个位置。
3) 将L(i)复制到L(k)。
代码:
void InsertSort(ElemType A[],int n)
{
int i,j;
for(i=2,i<=n;i++)
{
if(A[i]<A[i-1])
{
A[0]=A[i];
for(j=i-1;A[0]<A[j];--j)
{
A[j+1]=A[j];
}
A[j+1]=A[0];
}
}
}
代码分析:
说实话,初学此排序算法的时候,看到这个代码我是懵逼的,心中无数个疑问:为啥i=2? A[0]=A[i]?虽然以及明白了插入排序的思想,但是真正落实到代码,可就盖了帽了,那么我们就依次来分析分析这个让人晕厥的代码。

①②for(i=2;i<=n;i++)循环:
疑问①:i=2为什么是从第2个元素,也就是数组第3个位置开始的?
答:A[0]位置我们留做哨兵了,A[1]位置是排序元素的第一个元素,我们由中心思想知道:该数组分为3个部分:有序序列、待排元素、无序序列。所以我们知道,第一个元素很明显不需要排序,此刻它就是有序序列,自然而然,第二个元素就是第一个被排序元素,所以从i=2也就是A[2]开始排序。
疑问②: i<=n 为啥就不是ii
答:众所周知,for循环的第二个条件是用来判断循环终止的条件,即:我们要知道在排序过程中循环执行到哪里停止了,很明显,数组A[]中只有n个元素需要排序,自然而然,到第 n个元素截至。你写in个元素截至。
③if(A[i]
疑问③: 这个语句用意何在?
答:我们必须时刻谨记:该数组分为三个部分:有序序列、待排元素、无序序列 。所以:A[i]是我们的待排元素,而A[i-1]是我们的有序序列的最后一个元素(并且是有序中最大的元素)。如果我们的待排元素A[i]比有序最大的元素还大A[i-1],那么就不需要任何操作,反之:A[i]if语句进一步操作。
④A[0]=A[i]赋值语句:
疑问④: 为什么要把A[i]的值赋值给哨兵A[0]?为什么不是别的?
答:回顾中心思想,我们要在有序序列中插入一个元素,那么有序序列就应该向后移动一个位置,自然而然,A[i]就被A[i-1]覆盖了,未雨绸缪,我们就应该提前用哨兵把待插入元素A[i]给记录下来。
⑤ for(j=i-1;A[0]A[j+1]=A[j]循环语句的用意:
疑问⑤: 为什么有这个循环语句呢?
答:很明显此刻的A[0]就是待排元素,并且循环得初识条件是从i-1即:有序序列的最后一个元素开始的,所以很明显这个循环的目的是为了:在有序序列中给待排元素找到合适的位置,然后进行操作。并且这个位置就是A[j]。
疑问⑤: 为什么要让A[j+1]=A[j]呢?
答:很明显,每循环1次,如果能执行,我们就得把A[j]这个位置空出来,因为它可能是最终位置的预备役,然后把A[j]的位置给向右移动到A[j+1],直到找到一个最终的位置 ,**的,实在不好描述,不如去找个动画。这是来自:qinglv1的博客

⑥:A[j+1]=A[0]赋值语句
疑问⑥:A[j+1]=A[0],为啥不是:A[j]=A[0]?不是说A[j]才是最终位置吗?
答: 在for循环语句中,只要进入循环,就要最终执行j--语句,此刻的A[j+1]实则是A[j-1+1]的结果。我们来验证一下:
时间复杂度和稳定性分析:
空间效率: 仅仅使用了常数个辅助单元,因而空间复杂度为O(1)。
时间效率: O(n2) 最好情况:都有序,O(n) 最坏情况:与有序相反。
稳定性: 由于每次插入元素时总是从后向前比较再移动,所以不会出现相同元素相对位置发生变化地情况,所以是稳定的。
2、折半插入排序(顺序存储的表)
回顾直接插入排序算法:1)从前面的有序序列中找到待插入位置 2)将待插入元素复制到表中的插入位置
在算法中我们注意到:总是边比较边移动元素。所以我们引入了折半插入,即:先找到位置,然后统一地移动待插入位置之后的所有元素。
中心思想: 先折半查找出元素的待插入位置,然后统一地移动待插入位置之后地所有元素。
void InsertSort(ElemType A[],int n)
{
int i,j,low,high,mid;
for(i=2;i<=n;i++)
{
A[0]=A[i];
low=1;high=i-1;
while(low<=high)
{
mid=(low+high)/2;
if(A[mid]>A[0]) high=mid-1;
else low=mid+1;
}
for(j=i-1;j>=high+1;--j)
{
A[j+1]=A[j];
}
A[high+1]=A[0];
}
}
代码分析:
时间复杂度和稳定性分析:
上述算法看出,折半插入排序仅仅减少了比较元素的次数,约为:O(nlog2n),但是元素的移动次数未改变,他依旧依赖于排序表的初识状态。因此,折半插入排序的时间复杂度仍然是:O(n2);并且也是一种稳定的算法。
3、希尔排序(不稳定)
费事,希尔排序,也是换个花样玩插入排序,就不多赘述,直接上《王道考研》教材图:需要注意的是这是一种不稳定的排序方法

代码分析:
void ShellSort(ElemType A[],int n)
{
for(dk=n/2,dk>=1;dk=dk/2)
{
for(i=dk+1,i<=n;++i)
{
if(A[i]<A[i-dk])
{
A[0]=A[i];
for(j=i-dk;j>0&&A[0]<A[j];j-=dk)
{ A[j+dk]=A[j]; }
A[j+dk]=A[0];
}
}
}
}
时间复杂度和稳定性分析:
四、交换排序(冒泡,快排)
所谓交换,我初学的时候会有点疑惑,上面所提到的插入排序不是也涉及到交换元素了吗?其实到后续我们发现,真交换排序,每一次比较,都可能会然他交换位置。
1.冒泡排序
冒泡排序 (Bubble Sort) 一种交换排序,它的基本思想是:两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。冒泡的实现在细节上可以有很多种变化,我们将分别就3种不同的冒泡实现代码,来讲解冒泡排序的思想。这里,我们就先来看看比较容易理解的一段。
初阶冒泡排序:
void BubbleSort0(ElemType A[],int n)
{
int i,j;
for(int i=1;i<n,++i)
{
for(int j=i+1;j<n;++j)
{
if(a[i]>a[j])
{
swap(a[i],a[j]);
}
}
}
}
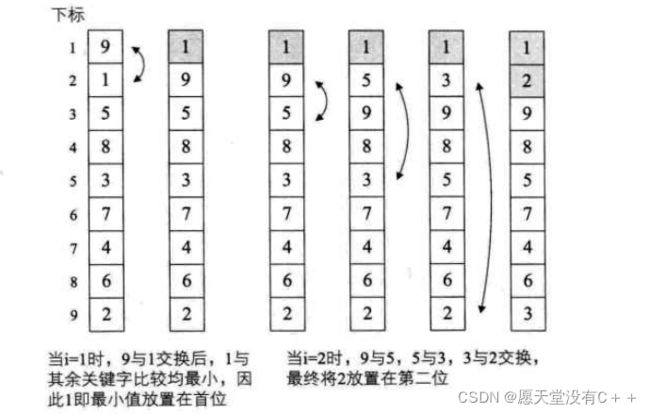
这段代码严格意义上来说,不算是标准的冒泡排序算法,因为它不满足“两两比较相邻记录”的冒泡排序思想,它更应该是简单的交换排序而已。它的思路就是让每一个关键字,都和它后面的每一个关键字比较,如果大则交换,这样第一位置的关键字在一次循环后一定变成最小值。
中阶冒泡排序:
void BubbleSort0(ElemType A[],int n)
{
int i,j;
for(int i=1;i<n,++i)
{
for(int j=n-1;j>=i;--j)//j是从后往前循环
{
if(a[j]>a[j+1])//若后者大于前者
{
swap(a[j],a[j+1]);
}
}
}
}
高阶冒泡排序:
void BubbleSort0(ElemType A[],int n)
{
int i,j;
Status flag=true;
for(int i=1;i<n&&flag=true,++i)
{
flag=false;//用户标记是否交换
for(int j=n-1;j>=i;--j)//j是从后往前循环
{
if(a[j]>a[j+1])//若后者大于前者
{
swap(a[j],a[j+1]);
flag=true;
}
}
}
}
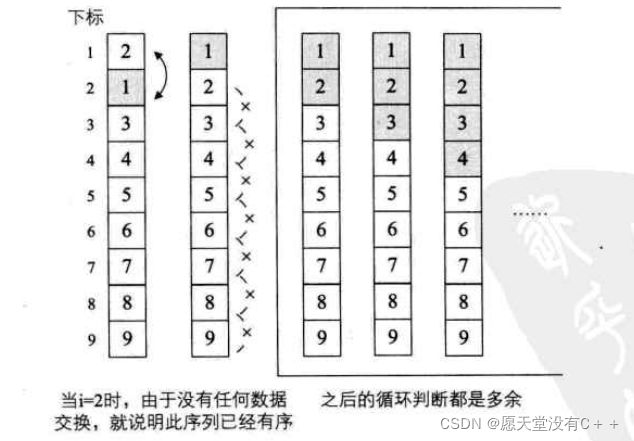
这样的冒泡程序是否还可以优化呢?答案是肯定的。试想一-下,如果我们待排序的序列是{2,1,3,4,5,6,7,8,9},也就是说,除了第一和第二的关键字需要交换外,别的都已经是正常的顺序。当i=1时,交换了2和1,此时序列已经有序,但是算法仍然不依不饶地将i=2到9以及每个循环中的j循环都执行了一遍,尽管并没有交换数据,但是之后的大量比较还是大大地多余了。所以设置一个flag来标记是否改变。
时间复杂度和稳定性分析:
空间效率: 仅仅使用了常数个辅助单元,因而空间复杂度为O(1)。
时间效率: O(n2) 最好情况:都有序,O(n) 最坏情况:与有序相反。
稳定性: 由于i>j且A[i]=A[j]时候,不会发生交换,所以是稳定的。
特点: 冒泡排序中所产生的有序子序列一定是全局有序的(不同于直接插入排序),也就是说,有序子序列中的所有元素的关键字一定小于或大于无序子序列中所有元素的关键字,这样每趟排序都会将一个元素放置到其最终的位置上。
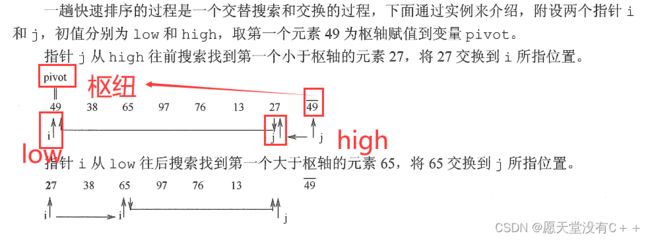
2.快速排序(重要)
一句话:快排是最经典,最牛的排序算法,学排序不学快排就白学了。