kmp算法详解-附java代码-长片杂谈

写在前面1

• 本片文章并不只是kmp学习的说教，虽然，也能帮助大家学习kmp，但是目的却不全是为了说明清楚kmp算法，它更多的是记录下我学习kmp算法过程中所遇到的种种问题，文章中很多的坑都是本人经历过的切实的问题，所以会出现许多啰嗦的话，显得整体比较冗长。
• 对于正在学习kmp遇到困难的朋友们，如果实在看不下去大佬们的博客，可以尝试来看看这一项杂谈，也许我遇到的问题，也是你们正在遇到的问题，当然也别抱太大希望哦~
• 对于已经学习过kmp算法的大佬们，也欢迎在评论区指正本文的不当之处。

写在前面2

• 最近刷题，碰到经典的kmp问题了，又忘记了怎么写了，正所谓教学相长也，所以这里边还是自己写一下总结，记录一下，顺便能帮助情况一样的小伙伴或者初来乍到的萌新们。

• 我也是看了一些博客滴，发现对萌新不太友好的地方有几个点，
  

  1. kmp的代码实现方式有多种，主要体现在前缀表的实现上(前缀表是啥后面会讲的)，有人用方案A，有人用方案B，虽然思路大体一致，但是由于代码对于萌新过于抽象，看了这个大佬的讲解没看明白，再换一个发现代码又不一样，几经周转，最后开始怀疑自己是不是不适合学编程…所以这里建议大家学习kmp算法的时候，就找一个大佬的帖子看，看明白为止，就不要轻易去换帖子了。
  2. 代码的设计会在实际的思路上有所优化(精炼)，其实kmp的思想还是比较好理解的，但是就是么几行代码，写出来就好像不是给人看的…实际上还是有一定的精炼的，但是很多大佬好像并没有对精炼的地方做一些基础的说明(可能觉得这是常识吧，反正我没看明白，憨憨难受o(╥﹏╥)o)。
  3. 大部分大佬讲解的比较细致，萌新表示篇幅太长无法接受，想看一些简单通俗的文章，快速上高速。em，这个怎么说呢，我个人感觉还是篇幅长一些的要好，毕竟kmp这种优秀的思想不是那么简单几句就能够说明白讲清楚的，就算真的能够说明白，大家也不见得就能看明白，大佬用心良苦啰嗦那么多也是有大佬的道理的嘛~，所以这里还是建议大家耐住性子，与其看一堆精简的文章最后还弄个半斤八两，倒不如来一篇精心熬制的大鸡汤来得实在。

• 话是这么说，我自己也是第一次写详解类文章，很多地方可能说的不太清楚，希望大佬们能慷慨指正。
  

什么是kmp？

• KMP名字的由来是由发明它的三个学者的名字首字母，感兴趣的同学们可以去了解一下，主要应用于字符串匹配上。
• kmp的主要思想是当字符串出现不匹配的情况时，可以知道之前已经匹配过的字符串，利用这些信息告诉指针下一次匹配应该回溯的位置
• 那么如何判断应该回溯到哪里呢？
• 在告诉大家判断之前，大家先要去了解一些辅助的知识点，什么是模式串，什么是主串(文本串)，什么是前缀，什么是后缀，以及前缀表。

模式串 & 主串(文本串)

• 模式串就是要在主串里面寻找的那个串，主串就是主串…
  
• 咳咳，语文水平有限，直接给大家上例子…

实现 strStr() 函数。
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

• 本题来自力扣28. 实现 strStr()，题中的haystack就是主串，needle是模板串。

前缀&后缀

• 本文这里的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

• 后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

• 话不多说，直接上例子：
  

• 这里有一个字符串aabaac，

• 前缀可以是a, aa, aab, aaba, aabaa。但是不能是自身(aabaac)

• 后缀可以是c, ac, aac, baac, abaac。但是不能是自身(aabaac)

前缀表（这东西很重要，请耐心看完，应该也不会很枯燥，应该…）

• 学习过kmp算法的小伙伴们一定都见过next数组，其实next数组就是一个前缀表(prefix table)，所以有些地方也有大佬用prefix来代换next，作为前缀表，本文就以next数组作为前缀表为例。

• 这里先说明一下，由于前缀表的实现方式八仙过海，版本不一，这里只介绍我常用的版本，对其他版本有兴趣的小伙伴们可以去看看别的大佬的博客~。

• 那么前缀表有啥用呢？

• 之前不是抛了个问题给大家嘛？“如何判断应该回溯到哪里呢？”

• 没错，前缀表就是用来辅助回溯到哪里的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

• 这边通过例子的形式来讲解前缀表的制作：

• 要在文本串(主串)：aabaabaacf中查找是否出现过一个模式串：aabaac，如图：
  

• 这边先模拟匹配的过程
  

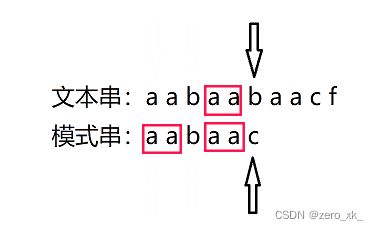
• 这边我把回溯的时候的关键的地方圈了一下，后面在进行讲解

• 不难看出在主串(文本串)中的第6个字符b和模式串的第6个字符f不匹配了。

• 如果自己暴力破解，指针回溯的时候就要从头来过了。

• 但是如果有前缀表，就不是从头开始，而是经过查询前缀表，告知指针要回溯的位置，然后从回溯的位置继续匹配。

• 那么前缀表到底是怎么制作的呢？

• 上面说了，当当前位置匹配失败了，前缀表会告诉你下一步匹配中，模式串指针应该要回溯到哪个位置。

• 其实前缀表会记录好下标i之前(包括i)的字符串中，有多大长度的相同前后缀。
  

• 咳咳，别着急，我只是把话引出来，毕竟网上不是有很多人说了嘛：“kmp 最长公共前后缀”。

• 其实这里应该理解为最长相等的前后缀，前缀表里面的回溯方法就是通过找最长相等的前后缀。

• 前后缀上面都讲了，最长 相等 前后缀，应该也不难理解吧。

• 那为啥前缀表通过这个最长相等的前后缀就能告诉指针该回退到哪里呢？

• 来来来，俺滴伏笔终于派上用场了(强行伏笔)
  
  

• 有没有发现之前匹配失败的时候，俺这里圈了两个，大伙看看模式串。

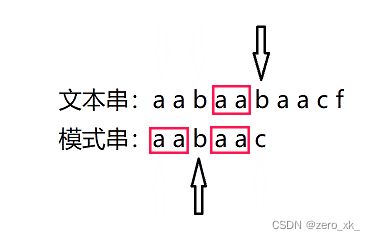
• 当前，在模式串的字符c这里匹配失败了，字符c的前面这几个字符串(也就是字符串aabbaa)的最长相等前后缀，也就是俺圈的这俩：aa，然后指针回退到这个前缀的后面一个位置(！！！！注意注意，这个地方画重点！！！后面算法实现会用到)就能继续进行匹配。

• 大家也注意到了，我在文本串(主串)也圈了这个aa。

• 对，这里有一个关系，前缀 等于 后缀 等于 文本串我圈的地方，下文称之为三角关系，咳咳。

• (这里的前缀/后缀是指，从模式串的第一个字符开始，到匹配出错的字符的前一个字符为止，所形成的的字符串，它的最长相等前后缀)

• 这个关系是巧合嘛？其实不是。

• 以下为原理部分，对你理解整个kmp非常重要，没看懂的多看几遍，纸上多画几遍，划重点，划重点！！！！后面实现的时候我就直接应用啦~

• 仔细想想，在匹配的过程中，除了出错的字符，已经匹配过的部分，模式串和文本串都是一样的。

• 所以，除了出错的字符，文本串中的后缀也会等于模式串中的后缀，而模式串中的前缀 == 模式串中的后缀(如果找得到最长相等前后缀的话)，文本串中的后缀自然也会等于模式串中的后缀啦。

• 正是因为这种三角关系，我们才能透过前缀表，来获取当当前匹配失败了之后，告诉模式串指针应该回溯到找到的最长相等前缀的下一项，利用三角关系，让我们省去模式串的前缀和文本串的后缀匹配的过程！！

• 这，就是三角关系的本质所在！

• 所以，以上的三角关系，不是巧合，而是有严谨的逻辑因果的，╭(╯^╰)╮。

前缀表制作实例

• 那么，理解完上面的关系，这里就直接上例子带大家理解一下，前缀表的制作。
• 还是那句话，这里的实现是我常用的版本。
• 下面先说一下我这里前缀表的实现方式：
  1. 首先前缀表的制作是针对于模式串，也就是说前缀表是由模式串生成的。
  2. 当模式串指针 j 出现匹配失败的情况，需要查找当前指针的前一项角标所映射的前缀表(即，查找next[j-1] )，以获取的要回溯的位置。
  3. next[j]的值的由来是根据最长相等前后缀中最长前缀中的最后一个字符的角标+1。
• 凭啥next[j]的值是这样来的？不太清楚的小伙伴们可以回去看看上面的三角关系，我有解释过。

• 咳咳，这不是给你们看例子来了嘛。

• 还是拿模式串：aabaac为例，如下：
  

• 首先，next[0] = 0，这里的next[0]是为了指示模式串指针在1的时候匹配出错要回退的位置(对照我上面标明的那句话和之前划重点让你们记下的笔记理解一下)。

• 也就是说当模式串在匹配到角标为1的位置上的时候出错了，查询当前指针的前一项角标所映射的前缀表，即next[1-1]，由于值为0，所以回溯到角标为0的位置。

• 对于这个要解释起来其实也不难。
  

• 当指针j在角标1的位置，前面只有一个字符a，之前在 前缀&后缀 说明了，前后缀是不包括自身的。

• 这里找不到最长前后缀，意味着在已匹配过的字符串中，没有可以利用的信息。

• 所以这里next数组(前缀表)应该指示指针回到初始位置，也就是角标为0的地方，也就是从头开始的意思。

---

• 对于next1]也是类似的分析，首先找到最长相等的前后缀。
  

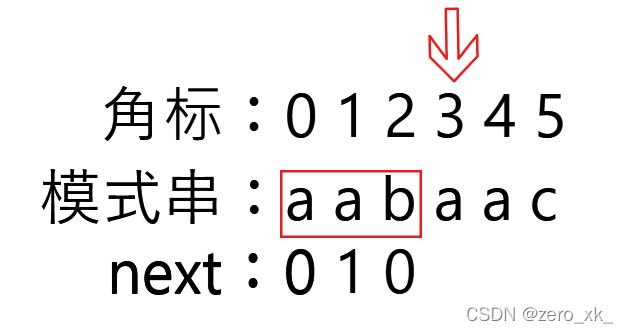
• 此时模式串的指针在角标为2的位置，这个时候，前面的字符串为aa，最长相等前后缀为"a"，其中，这里的前缀"a"中最后一个字符(‘a’)角标是0，而这边的实现规则是要告诉指针回溯到前缀串中最后一个字符的后面一个位置。

• 也就是说，所以此时前缀表存放的角标应该是0+1（0表示前缀"a"中最后一个字符(‘a’)角标，+1表示后一个位置），即，next[1] = 1。

• 如果在角标为2的位置出错了，之前说了，如果在j的位置匹配失败，应该查找next[j-1]，也就是查找，当前指针索引的前一项的前缀表。

• 所以这里应该查找next[2-1]，也就是next[1]，这不就对上咯~。

---

• next[2]也一样啦，首先找到最长相等的前后缀。
  

• 此时模式串的指针在角标为3的位置，这个时候，前面的字符串为aab，和最开始一样，找不到最长相等前后缀。

• 也就是说这里找不到最长前后缀，意味着在已匹配过的字符串中，没有可以利用的信息。

• 所以这里next数组(前缀表)应该指示指针回到初始位置，也就是角标为0的地方。

• 所以next[2] = 0；

---

• 之后的以此类推，成品如下，大家可以试着自己推一遍。
  
• 这里说一下前缀表最后一项的这个值，虽然next[5]的值在当前算法实现上来说无意义
• 因为不可能有在角标为len的时候出现模式串匹配失败的情况，越界了嘛，
• 但是不能说这个值计算出来没有意义，这个值本质上反应的是该模式串是否有最长相等前后缀。做过这道题的大佬们应该不会陌生，力扣459. 重复的子字符串。
• 这里也就提一下，不做细致讲解。如果只是出于查找模式串是否出现在文本串中，那到是可以不用算…
• 这边再附上前缀表做一次kmp运行演示吧(*￣︶￣)
  

代码实现

• 好了好了，长篇大论的原理也啰嗦完了，终于可以开始代码的编写了，下面我会带着大家跟着思路写一份稍微啰嗦的代码，然后在将它精简一下，也就是文章开篇说的精炼的地方，顺便也填一下坑。
• （ps：多种实现方式我就不填坑了，太啰嗦了…）
• 不过这里还是先说一句，还是请先把前面的理论捣鼓明白在来看，这会有助于代码的理解。
• 开干！
  
• 要实现kmp算法，分两大部分，第一完成前缀表的制作(next数组的制作)，第二，借助前缀表开始匹配主串与模式串。

生成 前缀表/next数组

• 根据前面的学习，相信大家对next数组有了一定的认识了。
• 这里还是要再啰嗦一下，这里的只是实现的一种方式，是有其他解法的。
• 生成next数组其实就是去计算模式串，跟着上面的思路还是比较好理解的，主要有如下3个步骤：
  1. 初始化
  2. 处理前后缀不同的情况
  3. 处理前后缀相同的情况
• 为了方便说明，这里将主串设为haystack， 模式串设为needle

---

1. 初始化

• 定义两个指针i, j；j负责指向前缀的最后一个字符的位置，i自然就负责后缀的最后一个字符的位置咯~

  • 这里还是对前后的概念说一下，怕有些傻娃分不清。
    

  • 咳咳，本文的前后缀的前后统一定义为左边为前，右边为后。

• 然后还要对next数组进行初始化，代码如下：

  	next[0] = 0;
  	int j = 0, i = 1;
  

• 这边说明一下这样初始化的原因，
• 首先来说这个next[0] = 0;，在前面的 前缀表制作实例 中我有展示到next[0]值的由来，因为next[0]，制作的时候前面找不到最长相等前后缀，所以没有找不到可以利用的信息，初始化为0也不足为奇了。
• 然后是int j = 0, i= 1;，这里对两个指针的初始化其实是为了计算出next[i]，也就是next[1].
• 前面也讲了，next[i]是用来指示当模式串在i+1项匹配出错时要回溯的地方，需要用到角0~i的字符串，去寻找最长相等前后缀，而j负责指向前缀的最后一个字符的位置，i负责后缀的最后一个字符的位置，对应的就是下图的情况。
  

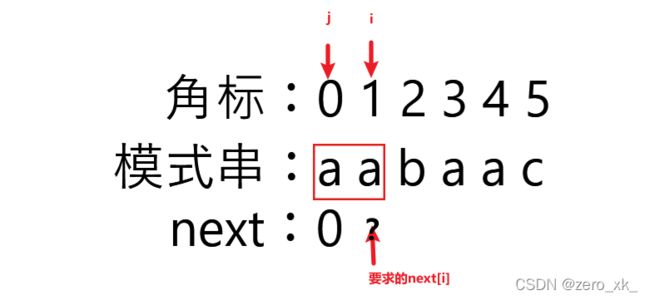
2. 处理前后缀不同的情况

• 上面初始化的时候也说了，j从0开始，i从1开始，进行前后缀的比较，也就是needle.charAt(i)与needle.charAt(j)的比较。
• 因为这里会使用到循环遍历模式串needle，所以开始的时候i的初始化可以放到for里面。

  	for(/*int i = 0;*/; i<needle.length(); i++){
  

• 为什么说needle.charAt(i)与needle.charAt(j)的比较就能代表整个前后缀的比较呢？
  • 这里其实是可以用数学归纳法/反证法证明的，我这边就不写出具体过程(太繁琐了)，就是口头讲一下思路，有兴趣的小伙伴们可以自己推导一下。
  • 前面也说了，j负责指向前缀的最后一个字符的位置，i负责后缀的最后一个字符的位置，为了让needle.charAt(i)与needle.charAt(j)的比较能代表整个前后缀的比较，我们需要保证这俩指针的前面所有字符都一样。
  • 仔细思考一下，当匹配到了需要判断needle.charAt(i)与needle.charAt(j)是否相等的时候，i与j负责的前后缀中的前面每一个字符都是经过这个判断相等后才会进行后面的判断。
  • 也就是说，既然都匹配到这里了，前面的字符都是匹配成功的。
• 那么，回到前面，如果 needle.charAt(i) 与 needle.charAt(j)不相同，也就是遇到前后缀末尾不相同的情况，就要向前回退。
• 如何回退呢？
• 不是有前缀表嘛(坏笑)，next[j-1]，就是记录了当在j处匹配错误的时候要回退的索引位置。
• 所以这里的处理代码如下：

	//注意一下这里使用的是while语句而不是if，
	//因为这里需要不断的去判断回溯，很多小伙伴们就是在这里用了if，然后bug找半天找不出问题
	while(j>0 && needle.charAt(i) != needle.charAt(j)){		//这里的j>0主要是防止next[j-1]发生角标越界
		j = next[j-1];
	}

3. 处理前后缀相同的情况

• 如果 needle.charAt(i) 与 needle.charAt(j) 相同，就意味着找到了最长相等前后缀了，那么就可以确定next[i]的值了，也即是next[i] = j+1;
• ps：这里留个坑，后面再填上。
• 为啥要+1，前面其实也解释过了，这边j代表的是前缀的最后一个字符的角标，我们next数组中存放的是要回溯的位置，自然是匹配的前缀的下一项啦，因为j本身就是匹配过的前缀中的一员嘛~
• 所以代码实现就是这样滴~

  	if(needle.charAt(i) == needle.charAt(j)) {
  		next[i] = j+1;
  	}
  

---

• 这边整理一下代码

  	//初始化next数组
      int j = 0;
      next[0] = 0;
      for(int i = 1; i<needle.length(); i++){
          while(j>0 && needle.charAt(i) != needle.charAt(j)) j = next[j-1];
          if(needle.charAt(i) == needle.charAt(j)) next[i] = j+1;
      }
  

• 细心的小伙伴们很快就发现了，这里还有一种情况没有处理，就是j<=0而导致的while循环结束，虽然这里的j不会为负数，因为next数组里面存放的都是角标，但是还有等于0的情况。
• 而此时因j == 0的条件退出循环，意味着needle.charAt(i) != needle.charAt(j)，也就是前面理论篇中介绍到的

  在已匹配过的字符串中，没有可以利用的信息。

• 由于这种情况没有处理，所以还需要增加一项判断处理代码，新增代码如下：

  	//初始化next数组
      int j = 0;
      next[0] = 0;
      for(int i = 1; i<needle.length(); i++){
          while(j>0 && needle.charAt(i) != needle.charAt(j)) j = next[j-1];
          if(needle.charAt(i) == needle.charAt(j)) next[i] = j+1;
          else if(j == 0) next[i] = 0;
      }
  

• 就在，大家以为万事俱备了，next数组初始化完成了，却忽视了一个细节，没错，就是我挖的坑，如果大家看到这里还没有发现漏洞，那只能说，前面的思路还是没有细品清楚~
• if(needle.charAt(i) == needle.charAt(j)) next[i] = j+1;
• 这串代码，实际上只注重了next数组值的获取，忘记了在循环中，j指针是需要后移的。
• 所以这里还要加上一个j++，新增代码如下：

  	//初始化next数组
      int j = 0;
      next[0] = 0;
      for(int i = 1; i<needle.length(); i++){
          while(j>0 && needle.charAt(i) != needle.charAt(j)) j = next[j-1];
          if(needle.charAt(i) == needle.charAt(j)) {
          	next[i] = j+1;
          	j++;
         	}
          else if(j == 0) next[i] = 0;
      }
  

• 这个时候，我们再来看这个j++的代码不禁笑出了声，哪有这样写代码的啊…
• 于是乎我们稍加整理，得到到如下代码:

  	//初始化next数组
      int j = 0;
      next[0] = 0;
      for(int i = 1; i<needle.length(); i++){
          while(j>0 && needle.charAt(i) != needle.charAt(j)) j = next[j-1];
          if(needle.charAt(i) == needle.charAt(j)) {
          	next[i] = ++j;
         	}
          else if(j == 0) next[i] = 0;
      }
  

• 就在，大家以为万事俱备了，next数组初始化完成了，却忽视了…
  
• 咳咳，这次代码本身没问题，只是还能在精炼一点。(填坑ing)

  	while(j>0 && needle.charAt(i) != needle.charAt(j)) j = next[j-1];
     	if(needle.charAt(i) == needle.charAt(j)) {
     		next[i] = ++j;
  	}
     	else if(j == 0) next[i] = 0;
  

• 大家注意一下这一串代码，这里的if else实际上就是在处理while循环的两个出口，而这两个出口最后都会对next数组进行操作，还没看出来，那只能说，前面的思路还是没有…
  
• 咳咳，其实我们在做的无非就是在每一次循环任务内，通过指针i初始化next数组。
• 简而言之就是我们每一次循环的结果，一定要计算出next[i]的值（疯狂暗示）
• 也就是说，在循环的尾部一定会出现next[i] = 计算结果。
• 那么这个计算结果是什么？（不知道的快去翻笔记，翻重点！！！）
• 是找到的前缀和的末尾的下一项，找不到就是0
• 而j指针就是被设计去负责末尾的下一项，匹配不到也是0（疯狂暗示）。
• 直接上代码吧，我都不知道怎么暗示下去了…

      //初始化next数组
      int j = 0;
      next[0] = 0;
      for(int i = 1; i<needle.length(); i++){
          while(j>0 && needle.charAt(i) != needle.charAt(j)) j = next[j-1];
          if(needle.charAt(i) == needle.charAt(j)) {
              ++j;
          }
          next[i] = j;
      }
  

• 以上代码，就是现在网上比较常见的next数组实现的方式的一种了，嗯不会再改了…
  

---

使用next数组来匹配文本串

• 历经千辛万苦，终于来到最后的匹配环节了，思路和前面next数组的生成了类似。
• 只不过这里不是用自己匹配自己，而是用文本串和模式串之间的匹配。
• 友情提示：主串/文本串为haystack，模式串为needle, 原题在力扣28. 实现 strStr()。
• 还一样，站在单个字符的角度，分三大步：
  1. 初始化。
  2. 处理haystack[i]与needle.charAt(j)匹配失败的情况
  3. 处理haystack[i]与needle.charAt(j)匹配成功的情况
• 这里和上面的基本上差不多，我就直接上代码了。

       //初始化指针
       j = 0;
       for(int i = 0; i<haystack.length(); i++){
  		//处理haystack[i]与needle.charAt(j)匹配失败的情况
       	while(j > 0 && haystack.charAt(i) != needle.charAt(j))
               j =next[j-1];
          //处理haystack[i]与needle.charAt(j)匹配成功的情况
       	if(haystack.charAt(i) == needle.charAt(j))
           	j++;
          //结果控制
       	if(j == needle.length())
           	return i-needle.length()+1;
       }
  

• 这边就提几个点：
  1. 匹配失败的回溯情况一样，因为都要去查找next数组，才能回溯。
  2. 匹配成功的情况下，需要做的事情就有点不一样了，匹配成功，除了必要的对指针进行移动，以便继续下一项的匹配，还需要判断，整个模式串是否已经匹配完成了。

---

完整代码

	class Solution {
    public int strStr(String haystack, String needle) {
        //这里题目没说有没有为空的情况，所以我在这里加上了判断，但是实际上题目的测试里面是没有为空的情况的，所以这里注掉了。
        //养成判空，判0的习惯，这是一件好事。
        //if(haystack == null || needle == null ) return -1;
        /* 
            这里要考虑一下模式串长度为0的情况，
            模式串长度为0就意味着空串，主串只要不为空，就一定能在开始的位置匹配到，所以直接返回0
            这边选择直接返回，额不是让下面的代码去处理，主要是因为初始化这里用到了，next[0]，
            直接让下面的代码去处理会报错。
        */
        if(needle.length() == 0) return 0;
        int hLen = haystack.length(), nLen = needle.length();
        int[] next = new int[nLen];

        //初始化next数组
        int j = 0;
        next[0] = 0;
        for(int i = 1; i<nLen; i++){
            while(j>0 && needle.charAt(i) != needle.charAt(j)) j = next[j-1];
            if(needle.charAt(i) == needle.charAt(j)) ++j;
            next[i] = j;
        }

        //初始化指针
        j = 0;
        for(int i = 0; i<hLen; i++){
            while(j > 0 && haystack.charAt(i) != needle.charAt(j)) j = next[j-1];
            if(haystack.charAt(i) == needle.charAt(j)) j++;
            if(j == nLen) return i-nLen+1;
        }
        return -1;
    }
}

总结

• kmp算法的核心思想是当字符串出现不匹配的情况时，可以知道之前已经匹配过的字符串，利用这些信息告诉指针下一次匹配应该回溯的位置。
• 前缀表的使用，是kmp算法优于暴力算法的核心所在。
• kmp算法难就难在对前缀表的作用原理的疑惑，难以理解为什么前缀表的这样设计就能实现最优回溯，所以本文对原理部分也用了一定的篇幅去描述，希望能对小伙伴们有一定的帮助。

其他

• 既然kmp算法这么好用，那么以后用来查找字符串都用kmp就好了？
• 其实不然，虽然kmp算法拥有理论上良好的时间复杂度上限，但是我们现在所学的大部分语言中的字符串查询函数，却并没有使用kmp算法来实现。
• 这主要是由于厂商在实现函数的时候需要考量平均时间复杂度和最坏时间复杂度。
• 作为开发者，你会去因为一小块用户的需求，而去放弃一片更加庞大的用户需求嘛？
• 答案可想而知，虽然kmp在极限的地方远超暴力算法，以及BM算法，但是在平均时间复杂度上，还是另外二者更深一筹。

最后

• 学习的路上不可能一帆风顺，生命的旅程没有什么理所应当，灰心的时候，适时回头看看，曾经走过的荆棘，是否已然枯木生花？
• 感谢在屏幕前的你，读到了最后，第一次，写这么长的文章，不是为了完成作业…