深度学习入门——神经网络
神经网络
神经网络是一种受到人脑神经系统启发的机器学习模型。它由一系列相互连接的人工神经元组成,这些神经元以层次结构排列。每个神经元接收来自上一层神经元的输入,并根据权重和激活函数对输入进行加权处理,然后将输出传递给下一层神经元。
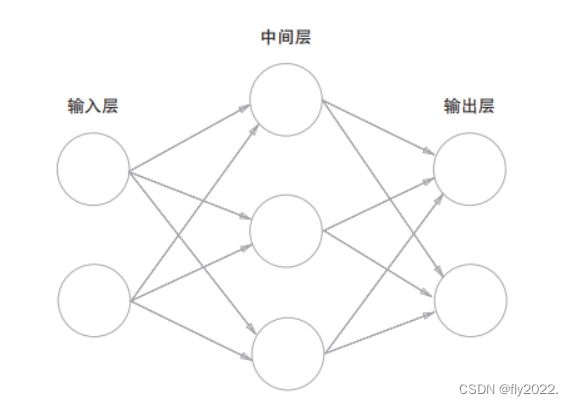
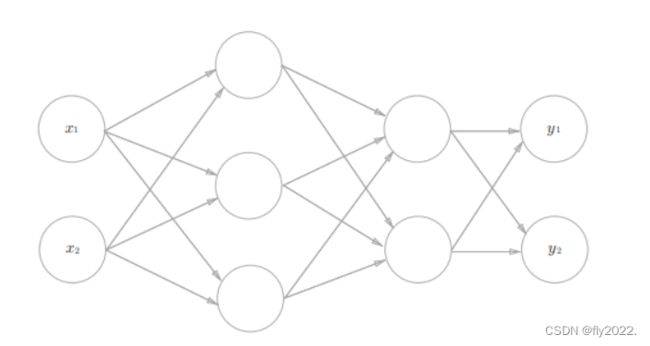
如下图是一个简单的神经网络,最左边的一列称为输入层,最右边的一列称为输出层,中间的一列称为中间层。
上述说到根据权重和激活函数对输入进行加权处理,这个过程可以描述成感知机实现的过程。
y = { 0 ( w 1 x 1 + w 2 x 2 + b ⩽ 0 ) 1 ( w 1 x 1 + w 2 x 2 + b > 0 ) y=\left\{\begin{array}{ll} 0 & \left(w_{1} x_{1}+w_{2} x_{2} + b \leqslant 0\right) \\ 1 & \left(w_{1} x_{1}+w_{2} x_{2} + b>0\right) \end{array}\right. y={01(w1x1+w2x2+b⩽0)(w1x1+w2x2+b>0)
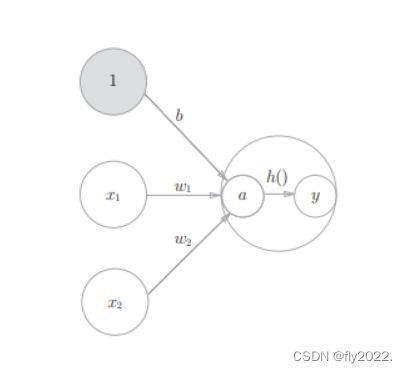
如上公式表示的感知机可以通过权重求和与一个函数h(x)实现。如下所示:
x = w 1 x 1 + w 2 x 2 + b x=w_{1}x_{1}+w_{2}x_{2}+b x=w1x1+w2x2+b
y = h ( x ) y=h(x) y=h(x)
h ( x ) = { 0 ( x ≤ 0 ) 1 ( x > 0 ) h(x)=\begin{cases}0(x\le 0) \\1(x> 0) \end{cases} h(x)={0(x≤0)1(x>0)
图示如下:
激活函数
阶跃函数
上述的激活函数以阈值为界,一旦输入超过阈值,就切换输出。这样的函数称为“阶跃函数”。
h ( x ) = { 0 ( x ≤ 0 ) 1 ( x > 0 ) h(x)=\begin{cases}0(x\le 0) \\1(x> 0) \end{cases} h(x)={0(x≤0)1(x>0)
对于阶跃函数的实现如下:
def step_function(x):
if x>0:
return 1
else:
return 0
上述实现只能接受实数,不允许参数为NumPy数组,支持NumPy数组的实现如下:
def step_function(x):
y = x > 0
return y.astype(np.int)
阶跃函数的图形如下
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x>0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
sigmoid函数
sigmoid函数是神经网络常用的一个激活函数,公式如下:
h ( x ) = 1 1 + e x p ( − x ) h(x)=\frac{1}{1+exp(-x)} h(x)=1+exp(−x)1
exp(-x)表示 e − x e^{-x} e−x的意思
python实现如下:
def sigmoid(x):
return 1 / (1 + np.exp(-x))
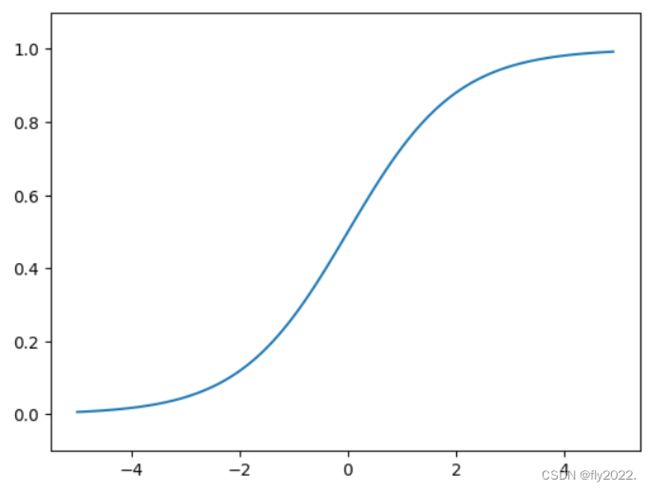
sigmoid图形如下:
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
两个激活函数的区别:
- 平滑性不同:sigmoid函数是一条平滑的曲线,输出随着输入发生连续性的变化。而阶跃函数以0为界,输出发生急剧性的变化。sigmoid函数的平滑性对神经网络的学习具有重要意义。
- 相对于阶跃函数只能返回0或1,sigmoid函数能够返回连续的实数,因此,相比起感知机中神经元之间流动的是0或1的二元信号,而神经网络中流动的是连续的实数值信号。
ReLU函数
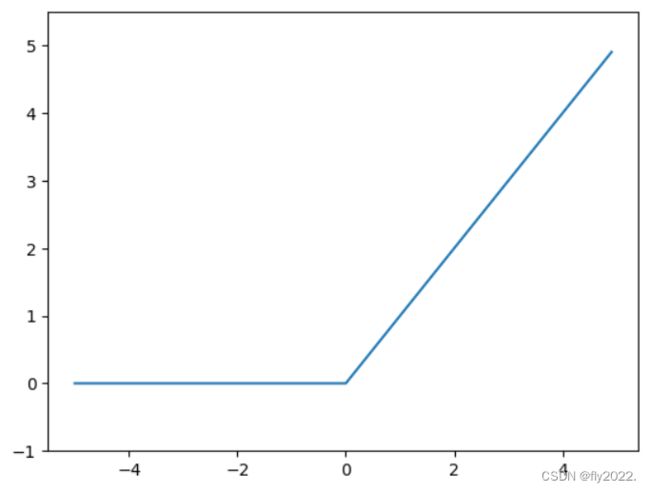
ReLU函数在输入大于0时,直接输出该值;在输入小于等于0时,输出0,公式如下:
h ( x ) = { x ( x > 0 ) 0 ( x ≤ 0 ) h(x)=\begin{cases}x(x> 0) \\0(x\le 0) \end{cases} h(x)={x(x>0)0(x≤0)
python代码实现:
def relu(x):
return np.maximum(0, x)
ReLU图形如下:
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1, 5.5)
plt.show()
非线性函数
阶跃函数和sigmoid函数还有其他共同点,就是两者均为非线性函数。sigmoid函数是一条曲线,阶跃函数是一条像阶梯一样的折线,两者都属于非线性的函数。
神经网络的激活函数必须使用非线性函数。因为,线性函数存在一个问题,不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。
举一个例子,如果我们考虑把线性函数 h(x) = cx 作为激活函数,把y(x) = h(h(h(x)))的运算对应3层神经网络。这个运算等价于 g ( x ) = c 3 x g(x) = c^{3}x g(x)=c3x作为激活函数的1层神经网络。
3层神经网络前向传播的实现
3层神经网络:输入层(第0层)有2个神经元,第1个隐藏层(第1层)有3个神经元,第2个隐藏层(第2层)有2个神经元,输出层(第3层)有2个神经元。流程如下图:
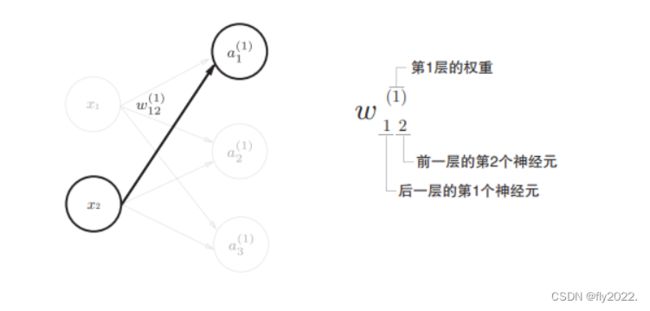
定义符号 w j k ( i ) w^{(i)}_{jk} wjk(i)为前一层第k个神经元到第i层第j个神经元 a j i a^{i}_{j} aji的权重,如下图:
代码实现如下:
def identity_function(x):
return x
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
z3 = identity_function(a3)
return z3
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) #[0.31682708 0.69627909]
输出层的设计
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出层的激活函数。一般而言,回归问题用恒等函数,分类问题用softmax函数。分类问题是数据属于哪一个类别的问题。。而回归问题是根据某个输入预测一个(连续的)数值的问题。
恒等函数和softmax函数
- 恒等函数会将输入按原样输出,对于输入的信息,不加以任何改动地直接输出。
- softmax函数的输出是0.0到1.0之间的实数。并且,softmax函数的输出值的总和是1。所以我们可以把softmax函数的输出解释为“概率”。
分类问题使用的softmax函数可以用下面的公式表示:
y k = e x p ( a k ) ∑ i = 1 n e x p ( a i ) y_k=\frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i)} yk=∑i=1nexp(ai)exp(ak)
python实现softmax函数:
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
softmax函数注意事项:softmax函数的实现中要进行指数函数的运算,但是此时指数函数的值很容易变得非常大。解决方法:令c为输入参数中的最大值,所有输入参数减去C后再做指数运算,这样等价于分子分母同时除以exp©,所以计算结果不变。改进代码如下:
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y