平衡树(AVL)详解
1. 为什么平衡树?
在二叉搜索树(BST,Binary Search Tree)中提到,BST树可能会退化成一个链表(整棵树中只有左子树,或者只有右子树),这将大大影响二叉树的性能。
前苏联科学家G.M. Adelson-Velskii 和 E.M. Landis给出了答案。他们在1962年发表的一篇名为《An algorithm for the organization of information》的文章中提出了一种自平衡二叉查找树(self-balancing binary search tree)。这种二叉查找树在插入和删除操作中,可以通过一系列的旋转操作来保持平衡,从而保证了二叉查找树的查找效率。最终这种二叉查找树以他们的名字命名为“AVL-Tree”,它也被称为平衡二叉树(Balanced Binary Tree)。
2. 原理
在节点上设置一个平衡因子BF,代表左右子树的高度差,BF = { -1, 0, 1}。
3. 旋转
AVL的Insert/Delete操作可能会引起树的失衡,可以通过选择解决这个问题。
3.1 4种旋转
(1)LL
(2)RR
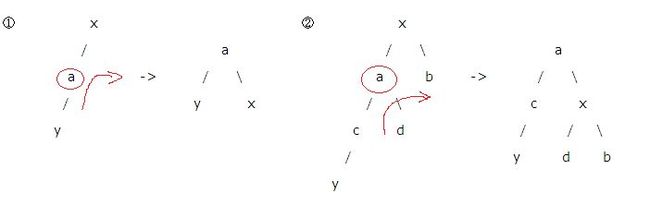
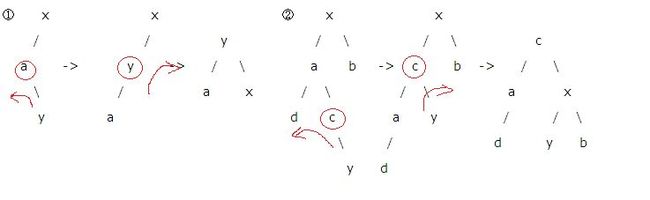
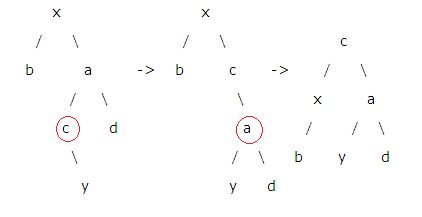
(3)LR
(4)RL
在下面的文章中有一个关于AVL选择的动画,大家不妨看看。
C#与数据结构--树论--平衡二叉树(AVL Tree)
3.2 旋转实现
在算法导论中给出旋转的伪代码:
LEFT-ROTATE(T, x) 1 y ← right[x] ▹ Set y. 2 right[x] ← left[y] ▹ Turn y's left subtree into x's right subtree. 3 p[left[y]] ← x 4 p[y] ← p[x] ▹ Link x's parent to y. 5 if p[x] = nil[T] 6 then root[T] ← y 7 else if x = left[p[x]] 8 then left[p[x]] ← y 9 else right[p[x]] ← y 10 left[y] ← x ▹ Put x on y's left. 11 p[x] ← y
//旋转以root为根的子树,当高度改变,则返回true;高度未变则返回false
private bool RotateSubTree(int bf)
{
bool tallChange = true;
Node root = path[p], newRoot = null;
if (bf == 2) //当平衡因子为2时需要进行旋转操作
{
int leftBF = root.Left.BF;
if (leftBF == -1) //LR型旋转
{
newRoot = LR(root);
}
else if (leftBF == 1)
{
newRoot = LL(root); //LL型旋转
}
else //当旋转根左孩子的bf为0时,只有删除时才会出现
{
newRoot = LL(root);
tallChange = false;
}
}
if (bf == -2) //当平衡因子为-2时需要进行旋转操作
{
int rightBF = root.Right.BF; //获取旋转根右孩子的平衡因子
if (rightBF == 1)
{
newRoot = RL(root); //RL型旋转
}
else if (rightBF == -1)
{
newRoot = RR(root); //RR型旋转
}
else //当旋转根左孩子的bf为0时,只有删除时才会出现
{
newRoot = RR(root);
tallChange = false;
}
}
//更改新的子树根
if (p > 0)
{
if (root.Data < path[p - 1].Data)
{
path[p - 1].Left = newRoot;
}
else
{
path[p - 1].Right = newRoot;
}
}
else
{
_head = newRoot; //如果旋转根为AVL树的根,则指定新AVL树根结点
}
return tallChange;
}
//root为旋转根,rootPrev为旋转根双亲结点
private Node LL(Node root) //LL型旋转,返回旋转后的新子树根
{
Node rootNext = root.Left;
root.Left = rootNext.Right;
rootNext.Right = root;
if (rootNext.BF == 1)
{
root.BF = 0;
rootNext.BF = 0;
}
else //rootNext.BF==0的情况,删除时用
{
root.BF = 1;
rootNext.BF = -1;
}
return rootNext; //rootNext为新子树的根
}
private Node LR(Node root) //LR型旋转,返回旋转后的新子树根
{
Node rootNext = root.Left;
Node newRoot = rootNext.Right;
root.Left = newRoot.Right;
rootNext.Right = newRoot.Left;
newRoot.Left = rootNext;
newRoot.Right = root;
switch (newRoot.BF) //改变平衡因子
{
case 0:
root.BF = 0;
rootNext.BF = 0;
break;
case 1:
root.BF = -1;
rootNext.BF = 0;
break;
case -1:
root.BF = 0;
rootNext.BF = 1;
break;
}
newRoot.BF = 0;
return newRoot; //newRoot为新子树的根
}
private Node RR(Node root) //RR型旋转,返回旋转后的新子树根
{
Node rootNext = root.Right;
root.Right = rootNext.Left;
rootNext.Left = root;
if (rootNext.BF == -1)
{
root.BF = 0;
rootNext.BF = 0;
}
else //rootNext.BF==0的情况,删除时用
{
root.BF = -1;
rootNext.BF = 1;
}
return rootNext; //rootNext为新子树的根
}
private Node RL(Node root) //RL型旋转,返回旋转后的新子树根
{
Node rootNext = root.Right;
Node newRoot = rootNext.Left;
root.Right = newRoot.Left;
rootNext.Left = newRoot.Right;
newRoot.Right = rootNext;
newRoot.Left = root;
switch (newRoot.BF) //改变平衡因子
{
case 0:
root.BF = 0;
rootNext.BF = 0;
break;
case 1:
root.BF = 0;
rootNext.BF = -1;
break;
case -1:
root.BF = 1;
rootNext.BF = 0;
break;
}
newRoot.BF = 0;
return newRoot; //newRoot为新子树的根
}
4. 插入与删除
4.1 插入
public bool Add(int value) //添加一个元素
{ //如果是空树,则新结点成为二叉排序树的根
if (_head == null)
{
_head = new Node(value);
_head.BF = 0;
return true;
}
p = 0;
//prev为上一次访问的结点,current为当前访问结点
Node prev = null, current = _head;
while (current != null)
{
path[p++] = current; //将路径上的结点插入数组
//如果插入值已存在,则插入失败
if (current.Data == value)
{
return false;
}
prev = current;
//当插入值小于当前结点,则继续访问左子树,否则访问右子树
current = (value < prev.Data) ? prev.Left : prev.Right;
}
current = new Node(value); //创建新结点
current.BF = 0;
if (value < prev.Data) //如果插入值小于双亲结点的值
{
prev.Left = current; //成为左孩子
}
else //如果插入值大于双亲结点的值
{
prev.Right = current; //成为右孩子
}
path[p] = current; //将新元素插入数组path的最后
//修改插入点至根结点路径上各结点的平衡因子
int bf = 0;
while (p > 0)
{ //bf表示平衡因子的改变量,当新结点插入左子树,则平衡因子+1
//当新结点插入右子树,则平衡因子-1
bf = (value < path[p - 1].Data) ? 1 : -1;
path[--p].BF += bf; //改变当父结点的平衡因子
bf = path[p].BF; //获取当前结点的平衡因子
//判断当前结点平衡因子,如果为0表示该子树已平衡,不需再回溯
//而改变祖先结点平衡因子,此时添加成功,直接返回
if (bf == 0)
{
return true;
}
else if (bf == 2 || bf == -2) //需要旋转的情况
{
RotateSubTree(bf);
return true;
}
}
return true;
}
4.2 删除
private void RemoveNode(Node node)
{
Node tmp = null;
//当被删除结点存在左右子树时
if (node.Left != null && node.Right != null)
{
tmp = node.Left; //获取左子树
path[++p] = tmp;
while (tmp.Right != null) //获取node的中序遍历前驱结点,并存放于tmp中
{ //找到左子树中的最右下结点
tmp = tmp.Right;
path[++p] = tmp;
}
//用中序遍历前驱结点的值代替被删除结点的值
node.Data = tmp.Data;
if (path[p - 1] == node)
{
path[p - 1].Left = tmp.Left;
}
else
{
path[p - 1].Right = tmp.Left;
}
}
else //当只有左子树或右子树或为叶子结点时
{ //首先找到惟一的孩子结点
tmp = node.Left;
if (tmp == null) //如果只有右孩子或没孩子
{
tmp = node.Right;
}
if (p > 0)
{
if (path[p - 1].Left == node)
{ //如果被删结点是左孩子
path[p - 1].Left = tmp;
}
else
{ //如果被删结点是右孩子
path[p - 1].Right = tmp;
}
}
else //当删除的是根结点时
{
_head = tmp;
}
}
//删除完后进行旋转,现在p指向实际被删除的结点
int data = node.Data;
while (p > 0)
{ //bf表示平衡因子的改变量,当删除的是左子树中的结点时,平衡因子-1
//当删除的是右子树的孩子时,平衡因子+1
int bf = (data <= path[p - 1].Data) ? -1 : 1;
path[--p].BF += bf; //改变当父结点的平衡因子
bf = path[p].BF; //获取当前结点的平衡因子
if (bf != 0) //如果bf==0,表明高度降低,继续后上回溯
{
//如果bf为1或-1则说明高度未变,停止回溯,如果为2或-2,则进行旋转
//当旋转后高度不变,则停止回溯
if (bf == 1 || bf == -1 || !RotateSubTree(bf))
{
break;
}
}
}
}