C语言函数递归的几道问题

一、什么是递归？

程序调用自身的编程技巧称为递归。

递归作为一种算法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程 序的代码量。

递归的主要思考方式在于：把大事化小。

二、递归的两个必要条件

1）存在限制条件，当满足这个限制条件的时候，递归便不再继续，所以通常使用if语句来确定递归出口。

2）每次递归调用之后越来越接近这个限制条件。

三、C语言函数递归的例题

①接收一个无符号整型值，按序打印它的每一位

思路：定义一个void型函数print，比如传入1234：

print（1234）-> 1 print(234) -> 1 2 print(34) -> 1 2 3 print(4) -> 1 2 3 4

代码：

void print(unsigned int n)
{
	if (n > 9)
	{
		print(n / 10);
	}
	printf("%u ", n%10);
}
int main()
{
	unsigned int n = 0;
	scanf("%u", &n);
	print(n);
	return 0;
}

②用函数递归求字符串长度

思路：定义int类型的函数my_strlen(const char* str)，接收的是字符串首地址

比如"abc"，求my_strlen("abc")

my_strlen("abc")   ->   my_strlen("bc")+1   ->   my_strlen("c")+1+1  ->   0+1+1+1

即my_strlen("abc") 的返回值是1+my_strlen("bc")

my_strlen("bc")的返回值是1+my_strlen("c")

my_strlen("c")的返回值是1+0（此时str+1碰到 ' \0 ' ）

代码：

int my_strlen(const char *str)
{
	if (*str == '\0')
	{
		return 0;
	}
	else return 1 + my_strlen(str+1);
}
int main()
{
	const char arr[] = "abc";
	int len = my_strlen(arr);
	printf("%d", len);
	return 0;
}

 

③递归求n的k次方（与n的阶乘类似）

思路：n^k = n * n^(k-1)  ，直到n^0=1

代码：

int pow(int n, int k)
{
	if (k == 0)
	{
		return 1;
	}
	return n * pow(n, k - 1);
}
int main()
{
	int n = 0;
	int k = 0;
	scanf("%d%d", &n, &k);
	printf("%d", pow(n, k));
	return 0;
}

④递归计算每一位数的和

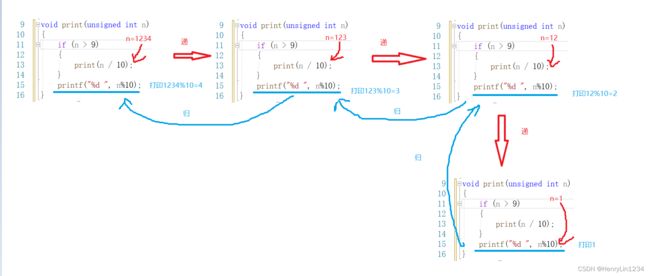
思路：定义int类型的函数DigitSum，比如接收1234

DigitSum(1234)   ->   1234%10+DigitSum(123) =4+(3+2+1)

DigitSum(123)    ->   123%10+DigitSum(12) =3+(2+1)

DigitSum(12)   ->   12%10+DigitSum(1)=2+(1)

DigitSum(1)返回自身的值，即1

代码：

int DigitSum(int n)
{
	if (n > 9)
	{
		return DigitSum(n / 10)+n%10;
	}
	return n;
 }
int main()
{
	
	int num = 0;
	scanf("%d", &num);
	int sum = DigitSum(num);
	printf("%d", sum);
	return 0;
}

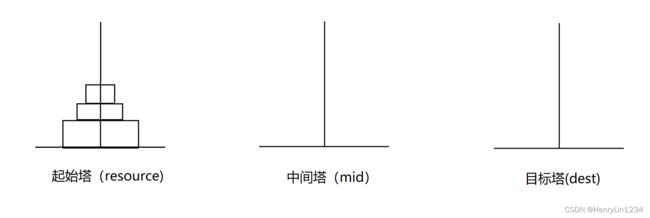
⑤汉诺塔问题

思路：我们只需要将移动的步骤打印出来，所以定义void类型的函数hanoi，接收参数为层数size，起始塔、中间塔、目标塔的名称，比如a、b、c。 

如果只有1层，那么直接从起始塔挪到目标塔就可以了;

如果有n层，根据汉诺塔问题的思路，将最下面的那一层和上面的n-1层看成两个整体，走三步：

第一步：将上面的n-1层从起始塔resource移动到中间塔mid，那么此时中间塔是目标塔

第二步：将最底下的第n层从起始塔resource移动到目标塔dest

第三步：将中间塔mid的n-1层移动到目标塔dest，那么此时中间塔是起始塔

所以我们不难发现，第一步和第三步需要进行函数递归。

void hanoi(int size,char resource,char mid,char dest)
{
	//如果只有1层，那就直接到目标塔
	if (size == 1)
	{
		printf("%c -> %c\n", resource, dest);
	}
	//如果大于2层，那就重复三个步骤
	else
	{
		//将n-1层移动到中间塔，塔的顺序是resource,dest,mid
		hanoi(size - 1, resource, dest, mid);
		//将第n层移动到目标塔
		printf("%c -> %c\n", resource, dest);
		//将n-1层移动到目标塔，塔的顺序是mid，resource，dest
		hanoi(size - 1,mid,resource,dest);
	}
}
int main()
{
	int n=0; 
	scanf("%d", &n);
	hanoi(n, 'a', 'b', 'c');
	return 0;
}

⑥递归逆序字符串

思路：逆序的基本思路就是一个交换的过程：

void reverse(char* s)
{
	int left = 0;
	int right = strlen(s)-1;
	while (left <= right)//交换
	{
		char tmp = s[left];
		s[left] = s[right];
		s[right] = tmp;
		left++;
		right--;
	}
}

如果用递归，我们要想清楚在递的过程做什么，在归的过程又做什么，同时递归的限制条件是什么，在每次递归的过程如何逼近这个限制条件。

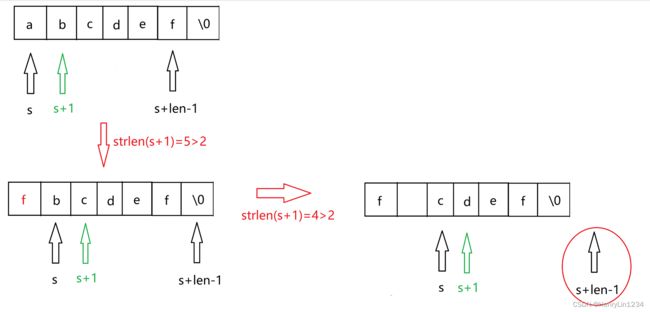
在非递归的代码中，left指针和right指针慢慢靠近，直到两者间没有字母，所以我们可以考虑在递归代码中这样考虑：我们将第一个字母a和最后一个字母f的交换看成一次逆序，此时形参s指向字母a的地址，如果a和f之间还有字母，也就是strlen(s+1)大于等于2，那么就递归逆序下去。

同时，我们在递的过程将前半部分的字母换为后半部分的字母，在归的过程中将后半部分的字母换为前半部分的字母，代码如下：

void reverse(char* str)
{
	int len = strlen(str);
	char tmp = *str;
	*str = *(str + len - 1);//递的过程将前半部分的字母换为后半部分的字母
	if (strlen(str + 1) >= 2)
	{
		reverse(str + 1);
	}
	*(str + len - 1) = tmp;//归的过程将后半部分的字母换为前半部分的字母
}

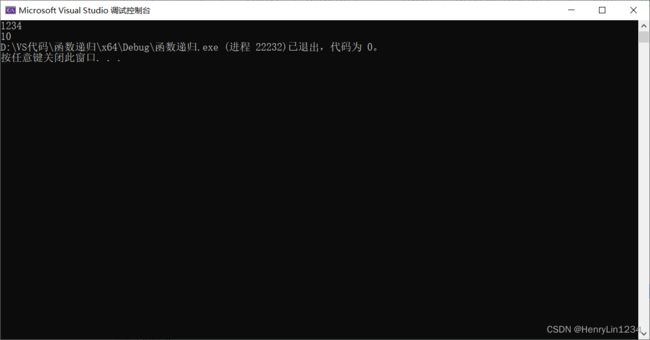
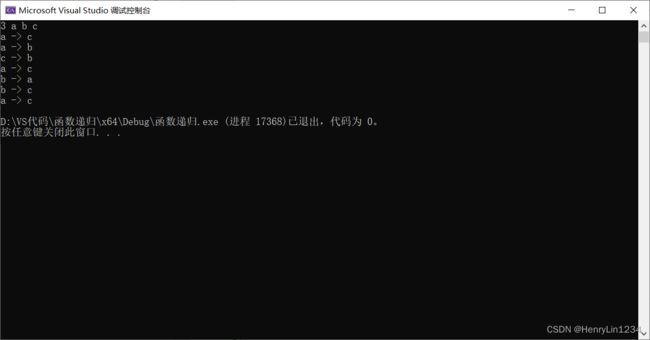
但是运行结果如下：

我们好像只成功完成了第一次逆序，也就是a和f的交换，中间的交换失败了，这是为什么？

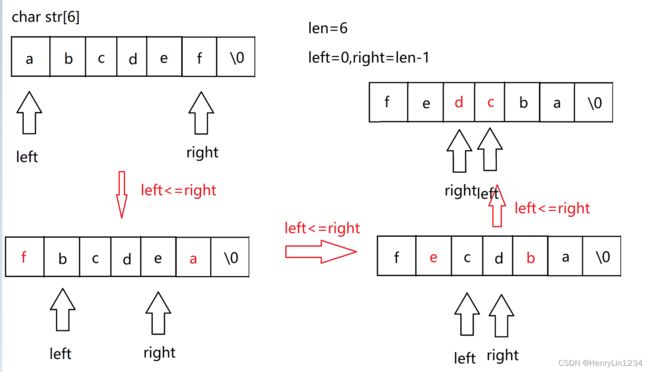
画图演示后，发现s+len-1越界了，于是导致了中间交换可能发生了一些错误。

那么我们再回过头来，我们想要的逆序是怎样的呢，首先得让s+len-1不越界，那么我们知道strlen函数碰到 '\0' 就会停止计数，而且我们要的strlen的区间应该是a和f之间的字母，那么就应该把f先置为 '\0' 。

所以我们每次递的过程，不仅要完成*s和*(s+len-1)的交换，而且要将*(s+len-1)='\0' 。

代码：

void reverse(char* str)
{
	int len = strlen(str);
	char tmp = *str;
	*str = *(str + len - 1);
	*(str + len - 1) = '\0';//关键的步骤
	if (strlen(str + 1) >= 2)
	{
		reverse(str+1);
	}
	*(str + len - 1) = tmp;
}