随机森林Proximity实现及应用

项目主页：randomforest
C++ implementation of random forests classification, regression, proximity and variable importance.
推荐阅读：Random Forests C++实现：细节，使用与实验

1 算法

1.1 随机森林Proximity简介

随机森林Proximity是一种表示两个样本相似性的度量。Proximity的应用方向包括异常数据检测(Outlier detection)、数据插补(imputation)、可视化等。最初的随机森林Proximity计算方法为，将所有的训练样本经过随机树到达叶子节点，如果两个样本到达同一个叶子节点，那么他们的Proximity值就增加1，最后结果除以树的数量以归一化。这种计算方法非常直接、快速，也被广泛使用。后续学者又提出了几种改进的方法，以提高Proximity估计的准确性，或更加适用于特定应用领域。

1.2 RF-GAP

2023年Jake S. Rhodes等在PAMI上发表了一篇论文《Geometry- and Accuracy-Preserving Random Forest Proximities》（arxiv）。他提出了一种新的随机森林Proximity（RF-GAP）计算方法，从理论上证明了基于该方法的分类/回归预测结果等同于oob分类/回归结果，并且给出了实验验证结果。2023年还能在PAMI上发表纯粹讨论随机森林的文章，且内容又是涉及RF算法中一个比较冷门的方面，说明这个工作是非常扎实的。

以下简要介绍下该论文的思想，文中Proximity（RF-GAP）的计算公式如下：

$$P(i,j)=\frac{1}{|T_{oob}(i)|}\sum _{t\in T_{oob}(i)}\frac{|\{j|inba{g}_t^{leaf}(i)\}|}{|\{inba{g}_t^{leaf}(i)\}|}$$
上述公式是根据我自己理解重写的，也可以参考论文中的公式，符号和表达式简要说明如下：

1. $|\cdot |$：表示集合中元素的数量；

2. $P(i,j)$: 样本$i$与$j$的Proximity值；

3. $T_{oob}(i)$: 随机树的集合，对于这些树样本$i$是out-of-bag(oob)数据；

4. $\{inba{g}_t^{leaf}(i)\}$: oob样本$i$落入树$t$的某个叶子节点，该节点上所有训练样本(in-bag)的集合；

5. $\{j|inba{g}_t^{leaf}(i)\}$: 上述叶子节点的in-bag样本中样本$j$的集合，有可能是0, 也有可能$\ge 1$，因为每棵树的训练样本是从原始数据集中有放回抽样得到的（bagging），所以叶子节点上的样本$j$数量可能大于1。

6. 需要说明的是，$P(i,j)\ne P(j,i)$，$P(i,i)=0$，${\sum }_{j}P(i,j)=1$。

1.3 实现代码

上述RF-GAP已经在我的randomforest上实现，分类与回归代码类似，以下仅贴出分类森林RF-GAP计算代码。

int ClassificationForestGAPProximity(LoquatCForest* forest, float** data, const int index_i, float*& proximities)
{
	if (NULL != proximities)
		delete[] proximities;

	proximities = new float[forest->RFinfo.datainfo.samples_num];
	memset(proximities, 0, sizeof(float) * forest->RFinfo.datainfo.samples_num);

	const int ntrees = forest->RFinfo.ntrees;
	int oobtree_num = 0;
	for (int t = 0; t < ntrees; t++)
	{
		//where the i-th sample is oob
		const struct LoquatCTreeStruct* tree = forest->loquatTrees[t];
		bool i_oob = false;
		for (int n = 0; n < tree->outofbag_samples_num; n++)
		{
			if (index_i == tree->outofbag_samples_index[n]) 
			{
				i_oob = true;
				break;
			}
		}

		if (false == i_oob)
			continue;

		oobtree_num++;

		map<int, int> index_multicity;
		const struct LoquatCTreeNode* leaf_i = GetArrivedLeafNode(forest, t, data[index_i]);
		
		if (leaf_i->samples_index != NULL)
		{
			for (int n=0; n<leaf_i->arrival_samples_num; n++)
			{
				if (index_multicity.find(leaf_i->samples_index[n]) == index_multicity.end())
					index_multicity.emplace(leaf_i->samples_index[n], 1);
				else
					index_multicity[leaf_i->samples_index[n]]++;
			}
		}else
		{
			// if forest did not store sample index arrrived at the leaf node, each in bag sample has to be tested
			for (int n = 0; n < tree->inbag_samples_num; n++)
			{
				const int j = tree->inbag_samples_index[n];
				const struct LoquatCTreeNode* leaf_j = GetArrivedLeafNode(forest, t, data[j]);
				if (leaf_i == leaf_j)
				{
					if (index_multicity.find(j) == index_multicity.end())
						index_multicity.emplace(j, 1);
					else
						index_multicity[j]++;
				}
			}
		}
		

		int M = 0;
		for (map<int, int>::iterator it = index_multicity.begin(); it != index_multicity.end(); it++)
		{
			M += it->second;
		}

		if (0 == M)
			continue;

		for (map<int, int>::iterator it = index_multicity.begin(); it != index_multicity.end(); it++)
			proximities[it->first] += it->second*1.0f/M;
	}

	if (0 == oobtree_num)
		return -1;

	for (int j = 0; j < forest->RFinfo.datainfo.samples_num; j++)
		proximities[j] = proximities[j] / oobtree_num;

	return 1;
}

2 应用

通过计算随机森林Proximity挖掘两个样本之间的相似度，可以应用于数据可视化、离群点检测、数据插补等场景。相比其他随机森林Proximity，据论文中描述RF-GAP在这些应用上展现了更好的效果。

2.1 离群点(outlier)检测

2.1.1 原理和实现

对于分类问题，离群点可以这样定义：该样本的outlier measure score显著地大于类内其他样本的值。这些异常样本可能与其他类别的样本相似，或者与所有类别样本都不相似。异常样本的存在会影响分类和回归算法的训练。随机森林离群点检测可以分为基于特征的方法和基于proximity的方法，前者比如Isolation Forest，基于RF-GAP的离群点检测方法属于后者。步骤如下：

1. 对于样本$i$，计算raw outlier measure score：$score(i)=\frac{n}{{\sum }_{j\in class(i)}{P}^2(i,j)}$
2. 计算类内raw_score的中值$m_c=median\{score(i)|class(i)\in c\}$，类内样本raw score与中值绝对差的均值$de{v}_c=\frac{1}{N_c}{\sum }_{class(i)\in c}|score(i)-m_c|$
3. 计算得到规范化的raw outlier measure score：$score(i)\leftarrow max(\frac{score(i)-m_c}{de{v}_c},0)$

在我的randomforest算法中实现计算outlier measure score的代码如下，过程细节借鉴了Leo Breiman的RF实现（Leo Breiman大神的代码是Fortran写的，关于outlier measure的计算在函数locateout中）。

int RawOutlierMeasure(LoquatCForest* loquatForest, float** data, int* label, float*& raw_score)
{
	if (NULL != raw_score)
		delete [] raw_score;
	
	int rv=1;
	const  int samples_num = loquatForest->RFinfo.datainfo.samples_num;
	const int class_num = loquatForest->RFinfo.datainfo.classes_num;

	raw_score = new float [samples_num];
	memset(raw_score, 0, sizeof(float)*samples_num);
	
	// 1. 计算raw outlier measure score
	float *proximities = NULL;
	for (int i=0; i<samples_num; i++)
	{
		ClassificationForestGAPProximity(loquatForest, data, i, proximities /*OUT*/);

		float  proximity2_sum = 0.f;
		for(int j=0; j<samples_num; j++)
		{
			if (label[j] != label[i] || j == i)
				continue;

			// within class
			proximity2_sum += proximities[j] * proximities[j];
		}
		
		raw_score[i] = samples_num / (proximity2_sum+1e-5);

		delete [] proximities;
		proximities = NULL;
	}

	// 2. 计算类内raw_score的中值，类内样本raw score与中值绝对差的均值
	float *dev = new float[class_num];
	float *median = new float[class_num];
	memset(dev, 0, sizeof(float)*class_num);
	memset(median, 0, sizeof(float)*class_num);

	for (int j=0; j<class_num; j++)
	{
		vector<float>  raw_score_class_j;
		
		for (int i=0; i<samples_num; i++)
		{
			if (label[i] == j)
				raw_score_class_j.push_back(raw_score[i]);
		}

		std::sort(raw_score_class_j.begin(), raw_score_class_j.end());

		const int sample_num_j = raw_score_class_j.size();
		if (0 == sample_num_j)
		{
			rv = 0;
			dev[j] = 1.f;
			median[j] = 1.f;
			continue;
		}

		if (sample_num_j%2 == 1)
			median[j] = raw_score_class_j[sample_num_j/2];
		else
			median[j] = 0.5f*(raw_score_class_j[sample_num_j/2] + raw_score_class_j[sample_num_j/2-1]);
		

		for (vector<float>::iterator it=raw_score_class_j.begin(); it != raw_score_class_j.end(); it++)
			dev[j] += abs(*it - median[j]);
		dev[j] = dev[j] / sample_num_j;
	}

    // 3. 计算得到规范化的raw outlier measure score
	for( int i=0, lb=0; i<samples_num; i++)
	{
		lb = label[i];
		raw_score[i] = RF_MAX( (raw_score[i] - median[lb])/(dev[lb]+1e-5), 0.0);
	}

	delete [] dev;
	delete [] median;

	return rv;
}

2.1.2 实验结果

使用mnist手写字符识别数据集训练随机森林分类器，样本数60000，特征数780。RF参数为：随机树 $T=200$，分类候选特征数 $\sqrt{780}$，节点最小样本数5，最大树深度40。
计算outlier measure的核心是计算proximities–$P(i,j)$，当训练RF时叶子节点保存了落入其中的in-bag样本信息（至少有样本在训练集中的序号），那么初略估计RF-GAP算法的复杂度为 $O(T\ast N)$，$T$与$N$分别是随机树和训练集样本的数量。RF-GAP文章最后作者提到这个算法比较适用于样本在几千范围的数据集，下一步工作是改进算法以适用于更大的数据集。
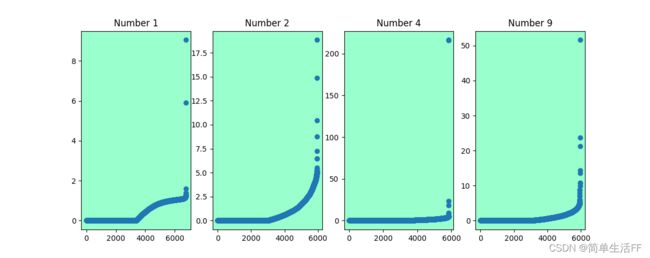
计算所有样本"outlier measure score"，其中部分类别样本的数值在下面图中展示（按数值升序），横坐标是样本，纵坐标是样本对应的"outlier measure score"。其中，类别4和9（即数字4–子图3，数字9–子图4）的极少数样本显著异常，可以对应查看下文中的离群样本图像，更加直观。

检测mnist手写数字识别数据集上离群样本，选取了几个类别中最大的raw outlier measure score对应的图像，从图像上来看确实较难辨认。比如数字4的离群样本，看起来是数字7，验证过确实标注类别4，在原训练集中的序号是59915 (序号从0开始)，raw score 超过200，与类内其他样本有显著区别。

随机选取了一些raw outlier measure score为0的样本图像（RF认为类内相似度较高），示例如下，确实是一些正常可辨认的手写数字。

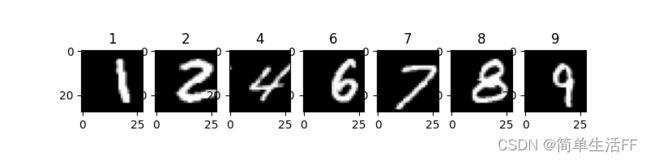
备注：mnist有几种训练集，对应特征有784维(对应图像28x28）和780维，本文选用的特征是780维。为了显示，在780维图像头部补4个0，使每个图像从780扩充到784，导致字符都有点偏右。

附录

使用我实现的randomforest算法进行RF训练+异常样本检测（计算样本的raw outlier measure score）的代码如下：

int main()
{
	// read training samples if necessary
	char filename[500] = "/to/direction/dataset/train-data.txt" 
	float** data = NULL;
	int* label = NULL;
	Dataset_info_C datainfo;
	int rv = InitalClassificationDataMatrixFormFile2(filename, data/*OUT*/, label/*OUT*/, datainfo/*OUT*/);
	// check the return value
	// 	... ...

	// setting random forests parameters
	RandomCForests_info rfinfo;
	rfinfo.datainfo = datainfo;
	rfinfo.maxdepth = 40;
	rfinfo.ntrees = 200;
	rfinfo.mvariables = (int)sqrtf(datainfo.variables_num);
	rfinfo.minsamplessplit = 5;
	rfinfo.randomness = 1;
	// train forest
	LoquatCForest* loquatCForest = NULL;
	rv = TrainRandomForestClassifier(data, label, rfinfo, loquatCForest /*OUT*/, 20);
	// check the return value
	// 	... ...

	//outlier measurement//
	float *raw_score=NULL;
	RawOutlierMeasure2(loquatCForest, data, label, raw_score);
	// raw_socre -- outlier measurements
	// ... ...
	delete [] raw_score;
	/outlier measurement//

	// clear the memory allocated for the entire forest
	ReleaseClassificationForest(&loquatCForest);
	// release money: data, label
	for (int i = 0; i < datainfo.samples_num; i++)
		delete[] data[i];
	delete[] data;
	delete[] label;
	return 0;
}