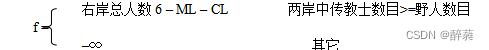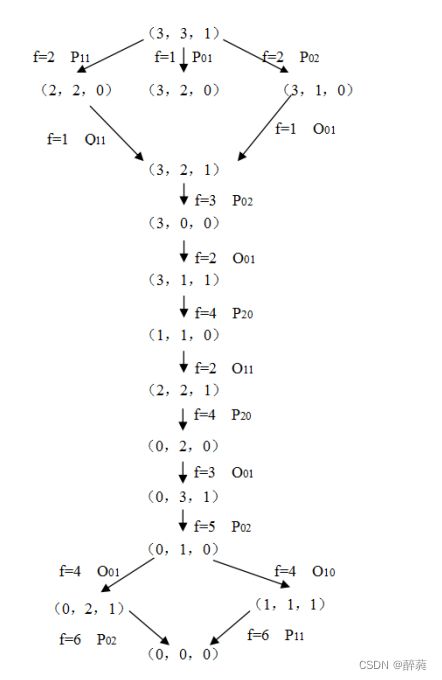传教士与野人过河问题（numpy、pandas）

努力是为了不平庸~

学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。

目录

一、问题描述

二、问题解释

1.算法分析

2.程序执行流程

3.编写程序对问题进行求解

三、问题思路

1. 算法分析：

2. 实验执行流程：

四、代码各步骤的方法、目的及意义

1. 导入库：

2. 获取输入：

3. 定义数据结构：

4. 判断状态是否合法：

5. 启发函数：

6. 判断两个状态是否相同：

7. 判断当前状态是否与父状态一致：

8. 对open列表按f值进行排序：

9. 在列表中查找节点：

10. A*算法主体：

11. 递归打印路径：

12. 主程序：

五、深入研究与代码优化

1.在一些输入情况下导致无限循环或内存消耗过大，为了更好地处理这些情况，可以添加一些额外的限制或优化措施。

2.经过研究，在野人与传教士过河问题中，以下两种优化策略更好：

3.这里以限制搜索深度为例，可以按照以下步骤进行：

 六、完整代码

---

一、问题描述

    有 N 个传教士和 N 个野人来到河边渡河，河岸有一条船，每次至多可供 k 人乘渡。问：传教士为了安全起见，应如何规划摆渡方案，使得任何时刻， 河两岸以及船上的野人数目总是不超过传教士的数目(否则不安全，传教士有可能被野人吃掉)。 即求解传教士和野人从左岸全部摆渡到右岸的过程中，任何时刻满足 M (传教土数) ≥ C 野人数)和 M+C≤k 的摆渡方案。 

二、问题解释

1.算法分析

设M为传教士的人数，C为野人的人数，用状态空间发求解此问题的过程如下：

M、C = N，boat = k，要求M>=C且M+C <= K

 用三元组来表示（ML , CL , BL）

其中0<=ML , CL <= 3 , BL ∈{ 0 , 1}

初始状态：河左岸有3个野人、3个传教士；河右岸有0个野人和0个传教士；船停在左岸，船上有0个人。初始状态（3，3，1）

目标状态：河左岸有0个野人和0个传教士；河右岸有3个野人和3个传教士；船停在右岸，船上有0个人。目标状态（0，0，0）

将整个问题抽象成怎样从初始状态经一系列的中间状态从而达到目标状态，状态的改变是通过划船渡河来引发的。

以河的左岸为基点来考虑

Pij：把船从左岸划向右岸，其中，第一下标i表示船载的传教士数，第二下标j表示船载的食人者数；

Qij：从右岸将船划回左岸，下标的定义同前。

则共有10种操作，操作集为F={P01，P10，P11，P02，P20，Q01，Q10，Q11，Q02，Q20}

规则集合

P10 if ( ML ,CL , BL=1 )   then ( ML–1 , CL , BL –1 )

P01 if ( ML ,CL , BL=1 )   then ( ML , CL–1 , BL –1 )

P11 if ( ML ,CL , BL=1 )   then ( ML–1 , CL–1 , BL –1 )

P20 if ( ML ,CL , BL=1 )   then ( ML–2 , CL , BL –1 )

P02 if ( ML ,CL , BL=1 )   then ( ML , CL–2 , BL –1 )

Q10 if ( ML ,CL , BL=0 )   then ( ML+1 , CL , BL+1 )

Q01 if ( ML ,CL , BL=0 )   then ( ML , CL+1 , BL +1 )

Q11 if ( ML ,CL , BL=0 )   then ( ML+1 , CL +1, BL +1 )

Q20 if ( ML ,CL , BL=0 )   then ( ML+2 , CL +2, BL +1 )

Q02 if ( ML ,CL , BL=0 )   then ( ML , CL +2, BL +1 )

根据要求，共得出以下5中可能的渡河方案：

　　（1）渡2传教士

　　（2）渡2野人

　　（3）渡1野人1传教士

　　（4）渡1传教士

　　（5）渡1野人

寻找一个启发式函数引导规则的选用

 　　本程序要定义状态结点，使用集合存储状态结点，使用递归的思想来寻找目标状态。

2.程序执行流程

上述原理完全是按照传教士和野人数量为3人，船一次的载客量最大为2为前提所得。结合上述分析不难看出，当尚未规定传教士和野人具体数量以及船一次最大载客量为多少时，与之前分析的差别仅仅在于根据人数不同，从河一端到另一端一共有多少中 载客方式，其他的原理流程与传教士和野人数量为3人，船一次的载客量最大为2的流程全部相同。

全部的可能状态共有32个，如表1所示。

            表1 传教士和食人者问题的全部可能状态

状  态	m, c, b	状  态	m, c, b	状  态	m, c, b	状  态	m, c, b
S0	3,3,1	S8	1,3,1	S16	3,3,0	S24	1,3,0
S1	3,2,1	S9	1,2,1	S17	3,2,0	S25	1,2,0
S2	3,1,1	S10	1,1,1	S18	3,1,0	S26	1,1,0
S3	3,0,1	S11	1,0,1	S19	3,0,0	S27	1,0,0
S4	2,3,1	S12	0,3,1	S20	2,3,0	S28	0,3,0
S5	2,2,1	S13	0,2,1	S21	2,2,0	S29	0,2,0
S6	2,1,1	S14	0,1,1	S22	2,1,0	S30	0,1,0
S7	2,0,1	S15	0,0,1	S23	2,0,0	S31	0,0,0

值得注意的是按照题目规定的条件，我们应该划去不合法的状态，这样可以加快搜索求解的效率。例如，首先可以划去岸边食人者数目超过传教士的情况，即Ｓ4、S8、S9、S20、S24、S25等6种状态是不合法的；其次，应该划去右岸边食人者数目超过修道士的情况，即S6、S7、S11、S22、S23、S27等情况；余下20种合法状态中，又有4种是不可能出现的状态；S15和S16不可能出现，因为船不可能停靠在无人的岸边；S3不可能出现，因为传教士不可能在数量占优势的食人者眼皮底下把船安全地划回来；还应该划去S28，因为传教士也不可能在数量占优势的食人者眼皮底下把船安全地划向对岸。可见，在状态空间中，真正符合题目规定条件的只有16个合理状态。

3.编写程序对问题进行求解

 

三、问题思路

1. 算法分析：

   传教士与野人过河问题中，假设传教士人数为M，野人人数为C，船的载客量为K。问题的状态空间如下：

   左岸：M、C

   右岸：0、0

   船始位置：左岸

   初始状态：左岸有M个传教士和C个野人，右岸无人，船停在左岸。

   目标状态：左岸无人，右岸有M个传教士和C个野人，船停在右岸。

   为了求解该问题，可以使用状态空间搜索和启发式函数。在船从左岸到右岸的过程中，可以根据以下规则选择船上的乘客：

   ①渡2个传教士

   ②渡2个野人

   ③渡1个野人和1个传教士

   ④渡1个传教士

   ⑤渡1个野人

   程序执行流程如下：

   ①定义合法状态集合，排除不符合条件的状态。

   ②使用状态空间搜索和递归的方法，通过一系列状态转换找到目标状态。

   ③根据启发式函数选择合适的规则来引导状态转换。

   ④对每个可能的状态进行遍历和判断，直到找到目标状态或无法找到解决方案。

   ⑤编写程序来求解问题并输出结果。

2. 实验执行流程：

   ①创建状态空间类，用于表示传教士与野人过河问题的状态。

   ②初始化初始状态和目标状态。

   ③定义合法状态集合，排除不符合条件的状态。

   ④使用深度优先搜索算法和递归方法，在合法状态集合中搜索有效路径。

   ⑤实现启发式函数，根据规则选择合适的状态转换。

   ⑥对每个可能的状态进行遍历和判断，直到找到目标状态或无法找到解决方案。

   ⑦编写程序来求解问题并输出结果。

四、代码各步骤的方法、目的及意义

1. 导入库：

   

    pandas用于数据处理和输出结果。

   numpy用于处理数组操作。

2. 获取输入：

    

   用户输入传教士数量、野人数量和船的最大容量。

3. 定义数据结构：

   

  

       child列表用于存储所有扩展节点。

   open_list用于存储待扩展的节点。

   closed_list用于存储已经扩展过的节点。

   State类表示状态节点，包含传教士数量、野人数量、船的位置等信息。

4. 判断状态是否合法：

   

   safe函数用于判断状态节点是否合法，根据一定的条件判断是否满足约束条件。

5. 启发函数：

    

   h函数是启发函数，用于评估节点的启发式值，这里使用的是传教士数量加野人数量减船的位置与船的最大容量的乘积。

6. 判断两个状态是否相同：

   equal函数用于判断两个状态节点是否相同，通过比较节点的属性值是否相等来确定是否相同。

7. 判断当前状态是否与父状态一致：

   back函数用于判断当前状态节点是否与其祖先节点一致，通过逐级回溯比较节点的属性值来确定是否一致。

8. 对open列表按f值进行排序：

  open_sort函数用于对open列表中的节点按照f值进行排序。

9. 在列表中查找节点：

  in_list函数用于在列表中查找是否存在与给定节点相同的节点。

10. A*算法主体：

    

 使用open_list存储待扩展的节点，使用closed_list存储已经扩展过的节点。

    循环中，首先检查是否存在目标节点，如果存在则添加到A列表中并从open_list中移除。

    如果open_list为空，则终止循环。

    从open_list中取出第一个节点，将其加入closed_list，然后根据船的位置在左右两岸生成新的子节点。

    检查子节点的合法性和是否与父节点一致，如果不满足条件，则移除该子节点。

    否则，设置子节点的父节点、更新g和f值，并将子节点加入open_list，然后对open_list进行排序。

    返回最终的目标节点集合A。

11. 递归打印路径：

    printPath函数用于递归打印路径，从目标节点开始回溯到初始节点，并打印每个节点的属性值。

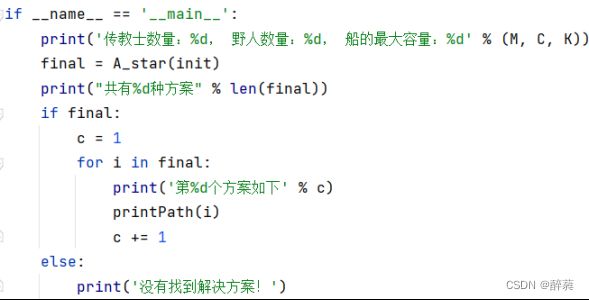
12. 主程序：

  主程序首先输出传教士数量、野人数量和船的最大容量。

    调用A_star函数获取最终的目标节点集合final。

    输出解决方案的数量。

    如果存在解决方案，则逐个输出每个解决方案的路径。

    如果没有找到解决方案，则输出相应的提示信息。

五、深入研究与代码优化

1.在一些输入情况下导致无限循环或内存消耗过大，为了更好地处理这些情况，可以添加一些额外的限制或优化措施。

①限制搜索深度：添加一个搜索深度的限制，防止程序无限地搜索下去。您可以设置一个最大搜索深度，并在搜索过程中进行检查。如果达到了最大深度但还没有找到解决方案，可以判断为无解或终止搜索。

②限制状态重复：在closed_list中记录已经访问过的状态节点，以避免重复访问。在扩展节点时，可以先检查新生成的节点是否已经在closed_list中出现过，如果是，则可以跳过该节点。

③优化启发式函数：通过调整启发式函数的计算方式，使其更加准确和高效。启发式函数的选择会影响搜索算法的效率和结果质量。您可以尝试不同的启发式函数来优化算法性能。

④剪枝策略：在生成新节点时，通过一些条件判断来剪除无效的分支。例如，如果在船上的野人数量多于传教士数量，那么这个状态是无效的，可以跳过。

⑤使用迭代加深搜索：迭代加深搜索是一种深度优先搜索的变体，它在每次迭代中逐渐增加搜索深度。这种方法可以在有限的搜索深度内找到解决方案，并且相对于完全深度优先搜索，它在空间上要求较少。

2.经过研究，在野人与传教士过河问题中，以下两种优化策略更好：

①限制搜索深度：通过设置最大搜索深度，防止程序无限地搜索下去。这可以帮助您控制算法的执行时间和资源消耗。您可以根据问题的规模和复杂性来确定最大搜索深度。如果搜索超过最大深度而没有找到解决方案，可以判断为无解或终止搜索。

②限制状态重复：在closed_list中记录已经访问过的状态节点，以避免重复访问。这可以防止算法在无效的状态之间反复循环。在扩展节点时，先检查新生成的节点是否已经在closed_list中出现过，如果是，则可以跳过该节点。

当然，具体使用哪种限制措施还要取决于需求和实际情况。如果对算法的执行时间有较严格的要求，那么限制搜索深度可能更适合。如果更关注算法的内存消耗，那么限制状态重复可能更为重要。

3.这里以限制搜索深度为例，可以按照以下步骤进行：

①在代码中添加一个变量，表示最大搜索深度，例如 max_depth。

②修改 A_star 函数，使其在搜索过程中检查当前搜索深度是否超过最大深度。可以在进入下一层递归之前检查深度，并在超过最大深度时终止搜索。您可以在合适的位置添加以下代码段：

if get.g > max_depth:

    # 超过最大深度，终止搜索

    break

③在主函数中设置最大搜索深度的值，例如 max_depth = 10。

通过设置最大搜索深度，可以控制算法的执行时间和资源消耗。根据问题的规模和复杂性，能够根据需求适当调整最大深度的值。

注意，修改搜索深度只是一种简单的限制措施，可以帮助控制算法的执行时间。但这也可能导致在某些情况下无法找到解决方案，因为可能没有足够的深度来搜索到最优解。因此，使用时需要权衡时间要求和解决方案的质量。

 六、完整代码

传教士与野人过河问题（numpy、pandas）可自定义输入有完整代码A*算法资源-CSDN文库