You only need to look at once 系列用于目标计数?——Object Counting:You Only Need To Look At One论文笔记
You only need to look at once 系列用于目标计数?——Object Counting:You Only Need To Look At One 论文笔记
- 一、Abstract
- 二、引言
- 三、相关工作
- 四、方法
-
- 4.1 问题定义
- 4.2 特征关联
- 4.3 特征提取和尺度聚合
- 4.4 训练损失
- 五、实验
-
- 5.1 实施细节与评估标准
- 5.2 数据集
-
- FSC-147
- MS-COCO
- 5.3 与其他少样本计数的方法进行比较
- 5.4 讨论
-
- 各组件的贡献
- 收敛速度
- 与目标检测的方法进行比较
- 六、结论
- 参考文献推荐
写在前面
这是第二篇关于目标计数的文章,站在 上一篇的肩膀上,思路比较简单,重点在于模型的搭建,创新点也是比较足。
- 论文地址:Object Counting:You Only Need To Look At One
- 代码链接:暂无,等待开源~
- 预计提交于 CVPR2022
- 第一次更新:2022年5月3日,看了一些文章,本文归属于 类别无关的单类别计数问题,即一张图片中只有一个类别,但是总的图库里面类别很多。
一、Abstract
本文旨在解决单次目标计数的问题,具体来说,仅采用包含一个示例样本bounding box的图像作为输入,来统计出该类别所有目标的个数。因此,本文提出了一种Look At One instance(LaoNet)网络来解决该问题。首先采用一个特征关联模块联合 自注意和关联注意力模块学习类内关系和类间关系,这使得网络能够对不同尺度目标更加鲁棒,然后再用一个尺度聚合机制提取不同尺度的信息。
二、引言
首先点出目标计数很重要,顺便强调下目前现有的难点:所有类别和标签的收集极其困难,进而引出少样本计数,而本文的工作正是上一篇少样本目标计数的拓展。接下来强调单样本计数存在的主要问题:1、目标计数任务中包含不同的类别,甚至一张图片里面就有多个类别,而在少样本计数中,这些类别在训练和推理阶段不会重叠;2、在单样本计数中,模型仅仅能从单个实例中学习;3、目标的尺寸、形状可能大相径庭。
本文提出的LaoNet主要由三个部分组成:特征提取、特征关联、密度回归。特征提取和特征关联旨在解决上面的挑战1、2。本文设计的特征关联模块得益于两种类型的注意力模块:自注意力和关联注意力,通过考虑所有存在的联系而解决了上述的问题。之后进一步提出尺度聚集机制来解决挑战3。
本文贡献如下:
- 设计了一种新颖的网络用于单样本目标计数,主要是自注意力机制和关联注意力机制;
- 提出了一种尺度聚合机制来提取更加全面的特征以及融合多尺度的box信息;
- FSC-147、COCO数据集在没有微调的情况下性能牛批。
三、相关工作
目标计数大致可分为基于检测的方法和基于回归的方法。缺点要么类别限定,要么需要大数据的标注,之后少样本计数出现了。而本文进一步提升为单样本计数。需要注意的是,当基于检测的方法用在少样本计数和单样本计数时,一般表现的很糟糕,可能的主要原因在于需要额外的所有实例标注。
四、方法
4.1 问题定义
单样本计数由一训练数据集 ( I t , s t , y t ∈ T ) \left(I_{t},s_{t},y_{t}\in \mathcal T\right) (It,st,yt∈T)和一序列集 ( I q , s q ∈ Q ) \left(I_{q},s_{q}\in \mathcal Q\right) (Iq,sq∈Q)组成,而模型的输入由一幅图像 I I I和一个Bounding box s s s组成。训练时, y t y_t yt 作为点标注提供;推理时,单样本 s q s_q sq和图像一起提供。
4.2 特征关联

基于自注意力与关联注意力模块来建立起特征关联,主要是多头注意力机制,以及层正则化。
之前的方法采用提供的Boxes特征作为内核来匹配目标类别的相似性,但是这极大依赖于样本的质量,因此本文提出特征关联模块用于学习query和支持的图像特征之间的关系,以及减轻不相关属性的限制,本质就是多头注意力外面套了两次层正则化以及FFN。
4.3 特征提取和尺度聚合
采用VGG-19作为backbone(?有点过于简单),取其最后一层输出直接展平后送入Self-Attention模块中。对于单样本,采用尺度聚合机制融合不同尺度的信息:
S = Concat ( F l ( s ) , F l − 1 ( s ) , … , F l + 1 − δ ( s ) ) S=\operatorname{Concat}\left(\mathcal{F}^{l}(s), \mathcal{F}^{l-1}(s), \ldots, \mathcal{F}^{l+1-\delta}(s)\right) S=Concat(Fl(s),Fl−1(s),…,Fl+1−δ(s))
其中, l l l为CNN的层数, F i \mathcal{F}^{i} Fi 为第 i t h i_{th} ith 层的特征图, δ ∈ [ 1 , l ] \delta\in[1,l] δ∈[1,l] 决定了聚合哪些层的特征。另外,加上位置特征以区分整合的尺度信息:
P E ( p o s j , 2 i ) = sin ( pos j / 1000 0 2 i / d ) P E ( p o s j , 2 i + 1 ) = cos ( pos j / 1000 0 2 i / d ) \begin{array}{l} P E_{\left(p o s_{j}, 2 i\right)}=\sin \left(\operatorname{pos}_{j} / 10000^{2 i / d}\right) \\ P E_{\left(p o s_{j}, 2 i+1\right)}=\cos \left(\operatorname{pos}_{j} / 10000^{2 i / d}\right) \end{array} PE(posj,2i)=sin(posj/100002i/d)PE(posj,2i+1)=cos(posj/100002i/d)
其中 i i i 是维度表示, p o s j pos_{j} posj 是第 j t h j_{th} jth 层特征图上的位置。
4.4 训练损失
采用欧几里得距离来衡量预测的密度图与GT密度图之间的差异,定义如下:
L E = ∥ D g t − D ∥ 2 2 \mathcal{L}_{E}=\left\|D^{g t}-D\right\|_{2}^{2} LE=∥∥Dgt−D∥∥22
其中 D D D为预测的密度图, D g t D^{gt} Dgt为GT密度图。为了提高局部样式一致性,还采用了 SSIM \textrm{SSIM} SSIM损失,最终总损失为:
L = L E + λ L S S I M \mathcal{L}=\mathcal{L}_{E}+\lambda \mathcal{L}_{S S I M} L=LE+λLSSIM
其中 λ \lambda λ为平衡权重。
五、实验
5.1 实施细节与评估标准
密度回归器由1个下采样层和3个带有ReLU激活的卷积层(2个1x1,1个1x1)组成,数据增强采用随机放缩和翻转,Adam优化器, l r = 0.5 × 1 0 − 5 lr=0.5\times10^{-5} lr=0.5×10−5,4个注意力头,两次self-attention+co-attention, δ = 2 , λ = 1 0 − 4 \delta=2,\lambda=10^{-4} δ=2,λ=10−4。
评估指标采用均方绝对误差Mean Absolute Error (MAE) 和均方根误差Root Mean Squared Error (RMSE):
M A E = 1 M ∑ i = 1 M ∣ N i g t − N i ∣ M A E=\frac{1}{M} \sum_{i=1}^{M}\left|N_{i}^{g t}-N_{i}\right| MAE=M1i=1∑M∣∣Nigt−Ni∣∣
R M S E = 1 M ∑ i = 1 M ( N i g t − N i ) 2 ) R M S E=\sqrt{\left.\frac{1}{M} \sum_{i=1}^{M}\left(N_{i}^{g t}-N_{i}\right)^{2}\right)} RMSE=M1i=1∑M(Nigt−Ni)2)
其中, M , N g t M,N^{gt} M,Ngt为图片的数量,GT计数的数量, N N N通过对预测的密度图求和得到。
5.2 数据集
FSC-147
这是上一篇计数文章里面的数据集,6135张图片,每张图片采用3个随机选择的BBox目标和其他的点目标作为标注。数据分布情况:训练集3659图片,89类别;验证集1286张图片,29类别;测试集1190张图片,29类别。
MS-COCO
将原来的COCO数据集划分为4个训练/测试分布,每个分布包含60个训练类别和20个测试类别,总共80个类别。
5.3 与其他少样本计数的方法进行比较
5.4 讨论
各组件的贡献
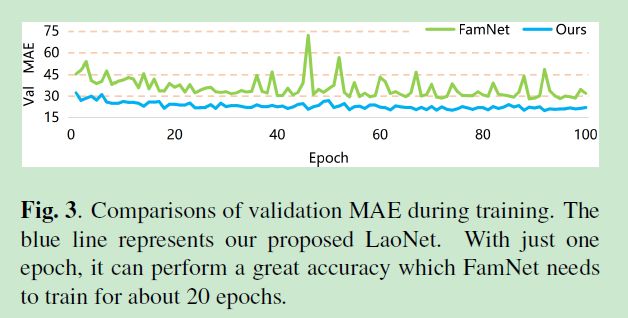
收敛速度
与目标检测的方法进行比较
六、结论
本文剑指单样本计数,只需模型看一眼某个实例就能统计该类别的个数;提出了LaoNet,由特征关联模块和尺度聚合模块组成,性能灰常好。
参考文献推荐
【1】Viresh Ranjan, Udbhav Sharma, Thu Nguyen, and Minh Hoai, “Learning to count everything,” in CVPR, 2021.
【2】 Shuo-Diao Yang, Hung-Ting Su, Winston H Hsu, and Wen-Chin Chen, “Class-agnostic few-shot object counting,” in WACV, 2021.
【3】Claudio Michaelis, Ivan Ustyuzhaninov, Matthias Bethge, and Alexander S Ecker, “One-shot instance seg mentation,” arXiv preprint, 2018.
写在后面
这篇工作是对之前少样本计数的拓展,模型结构换了,基本上算是正常的创新,接下来文章还有很多,仍需要大量阅读。