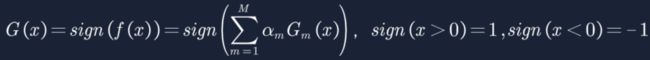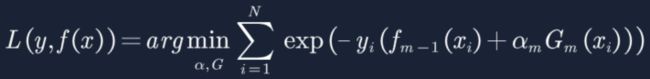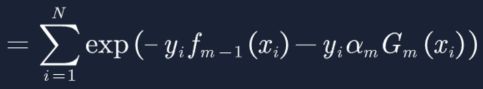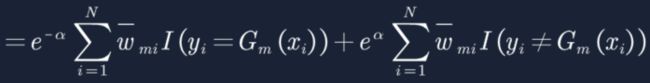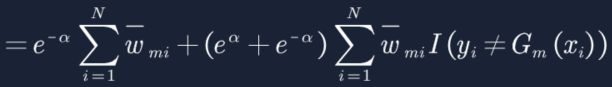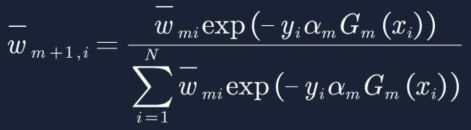Adaboost算法详细讲解
转自线上数据建模
Adaboost算法详细讲解
Adaboost(Adaptive Boosting):
Adaboost是Boosting模型,和bagging模型(随机森林)不同的是:Adaboost会构建多个若分类器(决策树的max_depth=1),每个分类器根据自身的准确性来确定各自的权重,再合体。同时Adaboost会根据前一次的分类效果调整数据权重。
具体说来,整个Adaboost 迭代算法分为3步:
1. 初始化训练数据的权值分布。如果有N个样本,则每一个训练样本最开始时都被赋予相同的权值:1/N。
2. 训练弱分类器(带有样本权重的分类器都可以,sklearn的AdaBoostClassifier采用的就是max_depth=1的决策树)。具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权值就被降低;相反,如果某个样本点没有被准确地分类,那么它的权值就得到提高,也就是如果某一个数据在这次分错了,那么在下一次我就会给它更大的权重。然后,权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
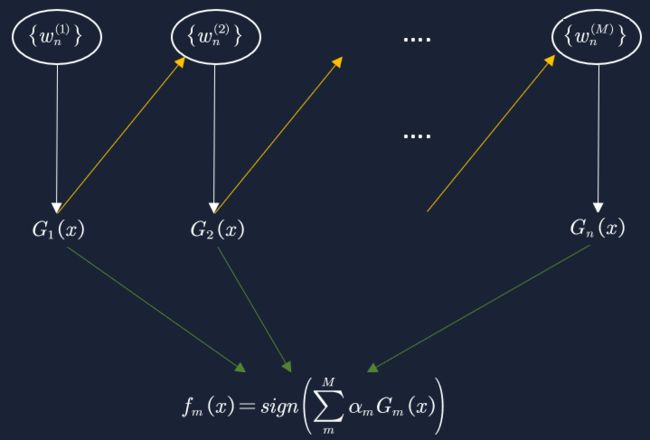
3. 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用, 而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。如下图所示,误差率低的弱分类器在最终分类器中占的权重(am)较大,否则较小。
接下来我们分两部分详细介绍Adaboost,分别从算法流程以及数据推导进行阐述。
Adaboost算法流程:
AdaBoost算法使用加法模型,损失函数为指数函数,学习算法使用前向分步算法。
1. 初始化每个训练样本的权值,共N个训练样本,每个样本的权重1/N。
2. 构建M个基分类器(决策树 max_depth=1),第m个分类器如下,am是第m个分类器的权重,分类器准确率高通常am权重也高,反之相反:
3. sign函数中的ΣamGm(x)>0时,sign返回+1,反之返回-1。
4. 计算误差率em,用没有分对的样本权重除以总权重,其中总权重(归一化)=1,字母I代表满足条件的=1,不满足条件的=0,如下,当Gm(xi)≠yi的样本对应的I=1,其他的样本对应的I=0。这个误差率em最终会作用到基分类器Gm(x)的权重am上面,下面我们就详细推导一下。
5. 接下来我们看一下em和am到底有什么关系?
6. 首先我们构建损失函数如下,当分类器预测正确时L(y,f(x))=e-1,预测错时L(y,f(x))=e,因此我们的损失函数是求极小值。
7. 由于我们是构建多个若分类器,通过sign函数将多个弱分类器加总在一起构建一个强分类器,因此分类器具备可加性。
8. 将上面的函数带入损失函数得:
9. 现在我们设![]() 等于下面的等式,用以带入上面的方程进行简化操作,需要强调一下,这里的
等于下面的等式,用以带入上面的方程进行简化操作,需要强调一下,这里的![]() 就是经过第m-1分类器调整后的样本权重w,换言之,就是样本权重w是由上一次基分类器调整后的结果进行调整,上一次分类越好的样本,
就是经过第m-1分类器调整后的样本权重w,换言之,就是样本权重w是由上一次基分类器调整后的结果进行调整,上一次分类越好的样本,![]() =e-1权重就越小;分类越不好的样本,
=e-1权重就越小;分类越不好的样本,![]() =e1权重就越大,这一点符合w优化要求,但是你可能会有疑问,此时更新后的样本权重之和≠1,
=e1权重就越大,这一点符合w优化要求,但是你可能会有疑问,此时更新后的样本权重之和≠1,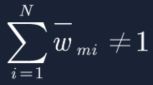 ,其实在公式推导层面,我们可以先不做归一化(下面会有讲到),可以等到公式推导完再对w进行归一化操作,因为此时是否做归一化不会对结果产生影响,后面会有证明。
,其实在公式推导层面,我们可以先不做归一化(下面会有讲到),可以等到公式推导完再对w进行归一化操作,因为此时是否做归一化不会对结果产生影响,后面会有证明。
11. 此时G(x)有两种情况,预测对y=G(x)和预测错y≠G(x),将两种情况带入方程:
12. 简化方程:
13. 提取常数项:
14. 字母I代表满足条件的=1,不满足条件的=0。
15. 同时加减函数:
16. 最终得到上面损失函数,求极值,老套路,对a进行求偏导,让偏导等于0:
17. 还记得我们的误差率em吗,公式如下所示,可以得到![]() 有没有做归一化都不会改变em的值(数学知识哈,分子分母同放大同缩小,值不变),既然em不变,那a也就不变,因此上面的公式推导,可以不对
有没有做归一化都不会改变em的值(数学知识哈,分子分母同放大同缩小,值不变),既然em不变,那a也就不变,因此上面的公式推导,可以不对![]() 做归一化:
做归一化:
18. 到此我们终于建立起分类器权重a与误差率e的关系,他们的关系是e越大,a越小,因此函数关系是反比关系,分类器越好(误差率低),权重应当越高。
19. 而接下来我们要算em,此时我们才需要对![]() 做归一化操作,公式也在告诉我们上一次分类器分的越好的样本,样本权重会减少,而分错的样本,样本权重会增加:
做归一化操作,公式也在告诉我们上一次分类器分的越好的样本,样本权重会减少,而分错的样本,样本权重会增加:
到此,我们知道了如何构建adaboost,其中包括如何更新w,以及找到了w,e和a的关系,接下来我们就尝试用实际的例子去构建adaboost,和传统例子不同,我们加入决策树作为若分类器,这一点和sklearn中的AdaBoostClassifier保持一致,很多网上关于adaboost的例子完全没有介绍真正的分类器是如何利用样本权重进行建树(决策树),只是通过简单的权重求和。因此为了能让大家充分了解adaboost是如何工作的,我就尝试将这两种方式(决策树 & 权重求和)通过对比的方式介绍给大家。
Adaboost具体实例:
求解过程:
1. 初始化训练数据的权值分布,令每个权值W1,i = 1/N = 0.1。
2. 构建弱分类器:
迭代过程1:
假设我们用CART二叉树算法对X进行切分,还记得决策树一节讲到的“对连续型变量如何构建二叉树吗?”通过遍历β,找到最佳切分点对X进行切分。如果不考虑GINI指数,只通过误差率来判断,β的遍历情况应该如下:
1)阈值β取2.5时误差率为0.3(x < 2.5时取1,x > 2.5时取-1,则6 7 8分错,误差率为0.3=3*0.1)
2)阈 值β取5.5时误差率最低为0.4(x < 5.5时取1,x > 5.5时取-1,则3 4 5 6 7 8皆分错,误差率0.6大于0.5,不可取。故令x > 5.5时取1,x < 5.5时取-1,则0 1 2 9分错,误差率为0.4)
3)阈值β取8.5时误差率为0.3(x < 8.5时取1,x > 8.5时取-1,则3 4 5分错,误差率为0.3)
后面的详细介绍,请关注原文“Adaboost算法详细讲解”