判断一个坐标点是否在不规则多边形内部
引射线法:从目标点出发引一条射线,看这条射线和多边形所有边的交点数目。如果有奇数个交点,则说明在内部,如果有偶数个交点,则说明在外部。
引射线法是项目中的常用算法,其他判断一个坐标点是否在不规则多边形内部还有:
面积和判别法:判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形,相等则在多边形内部。
夹角和判别法:判断目标点与所有边的夹角和是否为360度,为360度则在多边形内部。
主要说引射线法,因为项目中有应用到,其它两个方法也好理解。
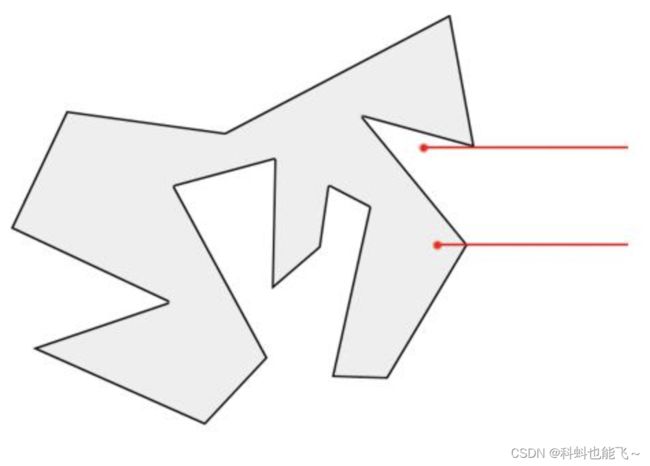
引射线法的具体做法:将测试点的Y坐标与多边形的每一个点进行比较,会得到一个测试点所在的行与多边形边的交点的列表。在下图的这个例子中有8条边与测试点所在的行相交,而有6条边没有相交。如果测试点的两边点的个数都是奇数个则该测试点在多边形内,否则在多边形外。在这个例子中测试点的左边有5个交点,右边有三个交点,它们都是奇数,所以点在多边形内。
为什么说目标点在多边形内部穿过多边形的线就有奇数个交点,而目标点在多边形外部穿过多边形的线就有偶数个交点呢?
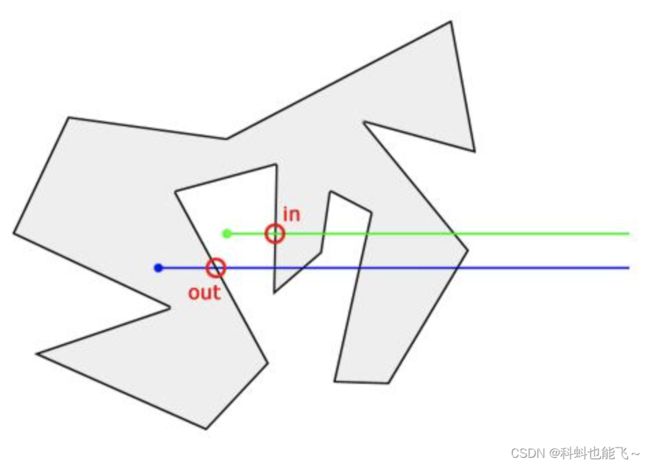
看下面这张图:
首先,多边形是个闭合的区域,一个点如果在多边形外(例如绿色的这个点),那么它穿过多边形必然是有进有出,这样它穿过多边形的交点就是2的倍数(偶数)
这个蓝色的点,因为它本身就在多边形区域内,所以,它开始就少了一个穿入多边形区域的交点,所以它与多边形的交点必然是奇数个。
特殊情况
1点在多边形的边上
射线法的主要思路就是计算射线穿越多边形边界的次数。那么对于点在多边形的边上这种特殊情况,射线出发的这一次,是否应该算作穿越呢?
判断点是否在线上的方法有很多,比较简单直接的就是计算点与两个多边形顶点的连线斜率是否相等,中学数学都学过。
2点和多边形的顶点重合
这其实是第一种情况的一个特例。
点和多边形顶点重合的情况更简单,直接比较点的坐标就行了。
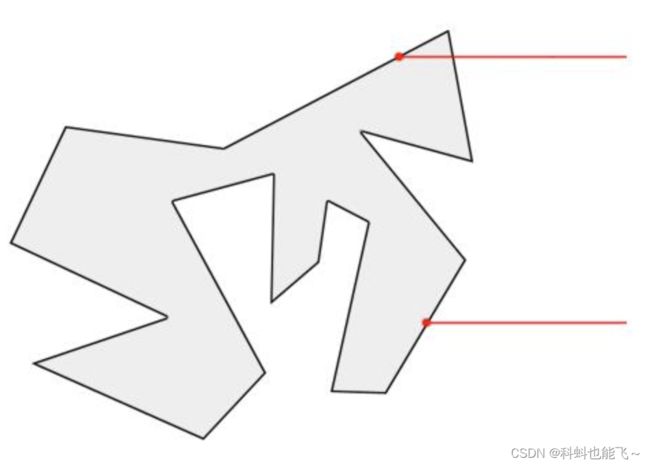
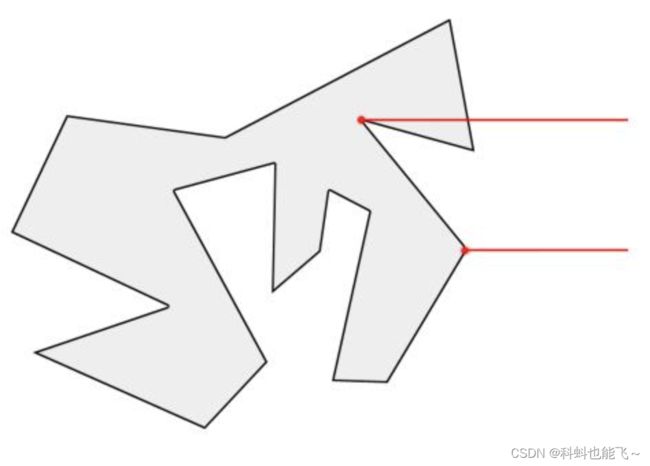
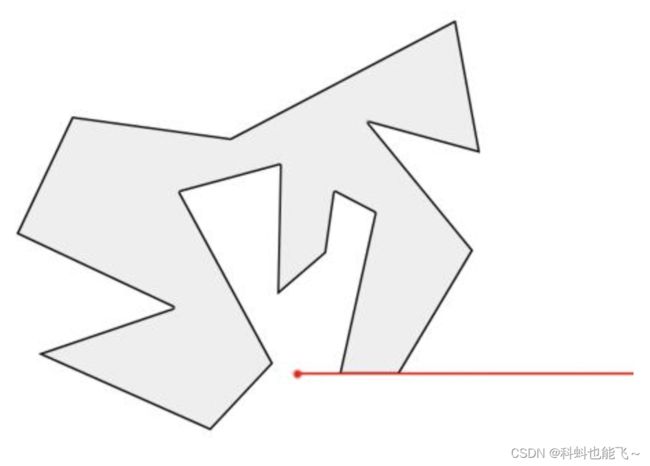
3射线经过多边形顶点 或者 射线刚好经过多边形的一条边
射线刚好经过多边形顶点的时候,应该算一次还是两次穿越?这种情况比前两种复杂,也是实现中的难点,后面会讲解它的解决方案。
顶点穿越看似棘手,其实我们换一个角度,思路会大不相同。
先来回答一个问题,射线穿越一条线段需要什么前提条件?没错,就是线段两个端点分别在射线两侧。只要想通这一点,顶点穿越就迎刃而解了。这样一来,我们只需要规定被射线穿越的点都算作其中一侧就可以。
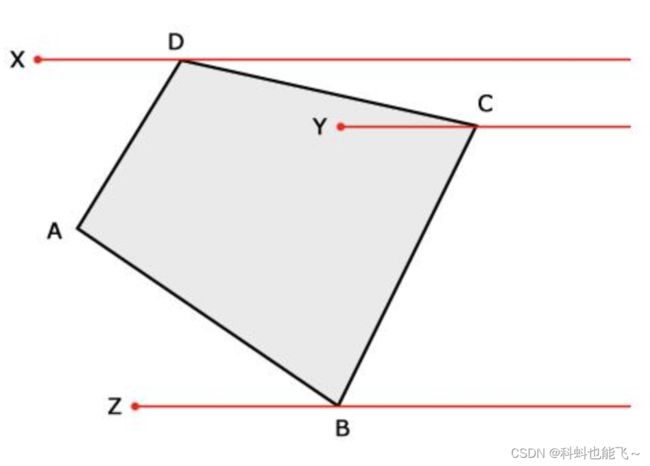
如下图,假如我们规定射线经过的点都属于射线以上的一侧,显然点D和发生顶点穿越的点C都位于射线Y的同一侧,所以射线Y其实并没有穿越CD这条边。而点C和点B则分别位于射线Y的两侧,所以射线Y和BC发生了穿越,由此我们可以断定点Y在多边形内。同理,射线X分别与AD和CD都发生了穿越,因此点X在多边形外,而射线Z没有和多边形发生穿越,点Z位于多边形外。
这样我们遇到的问题就都解决了。
接下来看一下项目带代码是怎么实现的:
需求是:一个点(使用经纬度表示坐标)是否在一个多边形内部,多边形有多个点构成,每个点是一个实际的经纬度坐标,有多个点构成一个多边形。
算法数学上实现思路: 判断一个点是在一个多边形内部的集中情况:
第一:目标点在多边形的某一个顶点上,我们认为目标点在多边形内部。
第二:目标点在多边形的任意一边边上,我们认为目标点在多边形内部。
第三:这种情况就比较复杂了,不在某一条边上,也不和任何一个顶点重合.这时候就需要我们自己去算了,解决方案是将目标点的Y坐标与多边形的每一个点进行比较,我们会得到一个目标点所在的行与多边形边的交点的列表。
解释一下第三点:
意思就是我们想象一个目标点,从目标点出发的一条水平向右的射线(这条射线取名为X),我们就能得到X与多边形的交点集合。
以上算法这三点做完我们就能得出结论:
如果第一和第二命中,那么直接就表面点在多边形内部
如果第一第二没有命中,那么判断第三,第三那条射线与多边形的交点个数为奇数则目标点在内部,偶数则目标点在外部
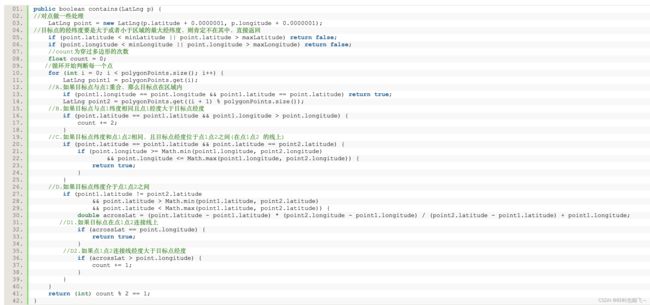
我们看一下公司项目解决这个问题的代码(代码原来是没注释的,都是我的理解手动给加上的,如有不对,请指点)
首先我们说明一点,点的集合是按照多边形的顺时针或者逆时针排列的,就是在列表中相邻的两个点组成的边在实际多边形中一定是真实存在这条边的,(列表第一个点和最后一个点组成的边也存在在多边形中),这一点是肯定的,如果不这样的话,那么这么多点组成的图形是完全不固定的,这就完全没有解决办法了(因为图形都不固定,何谈点在不在图形中呢)
在代码中有
A.如果目标点与点1重合,那么目标点在区域内
B.如果目标点与点1纬度相同且点1经度大于目标点经度
C.如果目标点纬度和点1点2相同,且目标点经度位于点1点2之间(在点1点2 连成的线上)
D.如果目标点纬度介于点1点2之间
D1.如果目标点在点1点2连接线上
D2.如果点1点2连接线经度大于目标点经度
其中A和C好理解;
我们想象一个目标点,从目标点出发的一条水平向右的射线(这条射线取名为X),而且我们假设经度向右增大;
B:对于B的情况,我们知道,目标点和点1在同一纬度上,我们假设目标点的经度小于点1的经度这样的情况下,射线X能经过点1,那么经过点1,我们需要给count+2,因为经过一个点,那么肯定就经过了这个点所在的两条变(两条直线相交确定一个点)
D:D的情况是目标点纬度介于点1和点2的纬度之间
D1:D1是D的一种情况,D1上面那个计算公式就是表明目标点和点1点2连成线段的位置关系,如果在点1点2连成的线段上,那么肯定在多边形区域内;
D2:D2是D1不存在的情况下,就是目标点不在点1点2连成的线段上,那么这样的情况下,如果目标点在点1点2连成的线段左侧,那么射线X与点1点2连成的线有交点,这样我们就需要给count+1,因为它只相交了一次,和B是不同的。
这样我们就能理解了计算点和多边形位置关系的算法
备注1:
我觉得上面项目中的代码B是无用的,因为:
代码最后返回的结果是
return (int) count % 2 == 1;
这个表达式明显和count值是奇数还是偶数有关,
而B是给count+2,这就没必要了,因为 奇数+2=奇数 偶数+2=偶数
所以给count值+2对最后的结果其实没有一点影响,这里只是为了表明算法的完整性(不+2 结果也不会出错)。
备注2:
在B和D2都有大于小于关系,这个关系是我们先设定好的,我们先就设定了经度向右增大,还设定了射线X是向右的;
如果我们设定不同,那么B和D2的大于小于关系也要相应的改变,但是B和D2肯定是要么都大于,要么都小于
并且备注1我们说过B其实不影响最后的结果,B改不改变对结果是没意义的,但是对算法本身是有意义的。